Понятие о двойственной задаче

Найти переменные x ₁, x ₂,…, x_n, которые максимизируют функцию

(Доб.1)

при ограничениях:

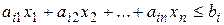, i=1,2,…,m, (Доб.2)

, j = 1, 2,…, n. (Доб.3)

Каждой задаче линейного программирования соответствует двойственная задача линейного программирования. Исходная задача называется прямой. Сформулируем правило построения двойственной задачи.

Каждой задаче линейного программирования соответствует двойственная задача, которая записывается по следующим правилам:

1. Каждому i -му ограничению исходной задачи соответствует переменная двойственной задачи u_i (двойственная переменная)

2. Каждой j -ой переменной исходной задачи соответствует ограничение двойственной. Матрица коэффициентов ограничений двойственной задачи является транспонированной матрицей ограничений исходной. Если в исходной задаче ограничения имеют знак £, то в двойственной - ³.

3. Коэффициенты при двойственных переменных в целевой функции двойственной задачи равны правым частям ограничений исходной задачи

4. Если исходная задача была на нахождение максимума, то двойственная будет на нахождение минимума:

	(Доб.4)
	(Доб.5)
	(Доб.6)

Или с заменой 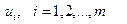на

(Доб.7)

(Доб.8)

(Доб.9)

Двойственная задача к двойственной = исходной!!!

===============================================================

Задание

Составить задачу ЛП (двойственную к исходной задаче о диете!)

Решить двойственную задачу о диете

А) Симплекс-методом

Б) с помощью «Поиска решения»

Выписать целевую функцию после окончания решения.

Убедится, что его нельзя улучшить.

Решение:

исходная задаче о диете

(Доб.10)

Ограничения по содержанию питательных веществ в рационе будут иметь вид:

	(Доб.11)
		(Доб.12)

двойственная задаче о диете	(Доб.13)
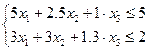
		(Доб.14)
		(Доб.15)

Описание смотри методичку!

раздел. 1.2.3. Реализация симплекс-метода (простейший случай)

С.19-25

	x1	x2	x3	x4	x5	b
x3		2,5
x4			1,3
F	-225	-150	-80
	Определяем ведущий элемент
	x1	x2	x3	x4	x5	b
x3		2,5
x4			1,3				0,666667
F	-225	-150	-80
	x1	x2	x3	x4	x5	b
x3		-2,5	-1,16667		-1,66667	1,666667
x1			0,433333		0,333333	0,666667
F			17,5

Дата добавления: 2015-07-11