Перестановка элементов массива

1 2 3 4 5 6 7 8 9

1 2 3 4 5 6

2 3 4 5 6

……

Чтобы указать элемент таблицы, нужно задать 2 индекса — номер строки (индекс i) и номер столбца (индекс j)

А[5,6]=11

Дан двухмерный массив вещественных чисел Т раз­мерностью 3 3.

Индексы столбцов Индексы строк
	0.5
			6.2
	8.3

Т[3,2] = 17,

Т[2,2] = 0.

В памяти элементы рас­полагаются следующим образом: Т[1,1], Т[1,2], Т[1,3], Т[2,1],.... Т[3,3].

Д. массивы широко используются в информатике, математике(при решении систем линейных уравнений), в экономике.

Задание размерности двухмерного массива.

Ученики сами решают, какие изменения нужно внести в алгоритмы работы с одномерными массивами, чтобы переделать их для двумерных.

1) Размерность задаётся константами:

Const

N=10;

M=20;

Var

x: array [1..n,1..m] of real;

2) Размерность задаётся переменными, значения которых вводятся с клавиатуры.

Var

x:array[1..50,1..50] of real;

N,M: byte;

...

Writeln(‘ Введите количество строк, столбцов n,m<=50’);

read(n,m);

…

Описание двумерного массива

VAR

<имя массива>: array [t1..t2,r1..r2] of <тип элементов>;

T1— номер первой строки;

T2 — номер последней строки;

R1 — номер первого столбца;

R2 — номер последнего столбца.

VAR

Т: array [1..3,1..3] of real;

Опишите двухмерный массив С, содержащий 3 строки и 6 столбцов символов:

TYPE

L = ARRAY[1..3,1..6] OF char;

VAR

C:L;

Ввод с клавиатуры элементов двумерного массива.

1. Элементы двухмерного массива лучше вводить в виде таблицы:

Чтобы ввести элементы одной строки массива можно воспользоваться вводом одномерного массива и повторять это для каждой строки.

Write ('Введите количество строк матрицы: ');

Readln(n);

Write(' Введите количество столбцов матрицы: ');

Readln(m);

Writeln;

Writeln(' Введите матрицу по строкам!');

for i: = 1 to n do

for j: = 1 to m do

Read(A[i,j])

Значения набираются через пробел с клавиатуры по строкам.

2.

Write ('Введите размерность матрицы: ');

Readln(n,m);

For i: = 1 to n do

For j: = 1 to m do

Begin Write (' A[',i,',’,j,’]=');

Readln (A[I,j])

end;

Элементы двухмерного массива можно генерировать с помощью функции случайных чисел:

{Генерация элементов матрицы с одновременным вы­водом их на экран по строкам:}

Randomize;

for i: = 1 to n do

begin

for j: = 1 to m do

begin

A[i,j]: = Random(51);

Write(A[i,j],' ')

end;

writeln

end;

Вывод элементов двумерного массива.

Массив должен выводиться таблицей.

{Внешний цикл — по номеру строки, внутренний — по номеру столбца в строке}

Writeln('Получена матрица:');

for i: = 1 to n do

begin

for i: = 1 to m do Write(A[i,j]:5:2);

Writeln

end;

Контрольные точки: определения массива, описание, ввод, вывод элементов массива.

Контрольные вопросы:

1) Можно ли назвать двухмерным массивом текст на странице,

коэффициенты системы линейных уравнений,

набор чисел 2 4 5 6 7?

2) Как определяется размерность двумерного массива в программе?

3) Как описывается двумерный массив?

4) Как осуществляется ввод двумернго массива?

5) Как должен выводится двумерный массив?

Какие повторяющиеся фрагменты можно выделить в программах, использующих двумерные массивы?

Основные алгоритмы работы с двухмерными массивами.

Ученики сами решают, какие изменения нужно внести в алгоритмы работы с одномерными массивами, чтобы переделать их для двумерных.

Пример1. Дан двухмерный массив размерностью К1 х К2. Найти в нём значение наибольшего элемента и его номера.

max: =A[1,1];

i_max: = 1;

j_max: = 1;

For i: =1 to k1 do

For j: =1 to k2 do

if A[i,j] >max then begin

max: =A[i,j];

i_max:=i;

j_max:=j;

end;

Запишите самостоятельно алгоритм нахождения минимального элемента и его индексов.

Пример2. Дан двухмерный массив размерностью К1 х К2. Найти количество элементов принадлежащих отрезку с границами А и В.

For i: =1 to k1 do

For j: =1 to k2 do

if (A[I,j]>=A) and (A[I,j]<=B) then k:= k+1;

Учащиеся затем решают, какие изменения нужно вносить, чтобы в задаче вычислялась сумма (среднее арифметическое) таких элементов.

Найти сумму отрицательных элементов двумерного массива.

Найти произведение неотрицательных элементов двухмерного массива.

Перестановка элементов массива

A[I,r] A[j,h]

B:= A[I,r];

A[I,r]:= A[j,h];

A[j,h]:=B;

Пример. Дан двухмерный массив А размерностью К1 х К2. Сформировать второй массив по правилу В=2*А+10.

Пример. Сформировать массив А, где элементами являются результаты таблицы умножения

Обобщение: напоминаются виды алгоритмов, которые рассмотрели.

Квадратная матрица. Индексы диагональных элементов матрицы

Поясняется понятие квадратной матицы, главной диагонали и соотношение индексов строк и столбцов, стоящих на главной диагонали.

Двухмерный массив с равным количеством строк и столбцов иногда называют квадратной матрицей.

(1,1) (1,2) (1,3) (1,4) (1,5)

(2,1) (2,2) (2,3) (2,4) (2,5)

(3,1) (3,2) (3,3) (3,4) (3,5)

(4,1) (4,2) (4,3) (4,4) (4,5)

(5,1) (5,2) (5,3) (5,4) (5,5)

1) i>=j 3) i+j<=n+1

2) i<=j 4) i+j >=n+1

Эле­менты квадратной матрицы с равными по значению индексами составляют главную диагональ. В нашем примере это элементы Т[1,1], Т[2,2] и Т[3,3].

Пример1. Дана квадратная матрица. Вычислить сумму элементов стоящих выше её главной диагонали.

Учащиеся затем решают, какие изменения нужно вносить, чтобы в задаче вычислялась сумма элементов, стоящих ниже главной диагонали (на главной диагонали), чтобы вычислялась среднее арифметическое элементов на главной диагонали (выше главной диагонали).

Пример 2. Сформировать из положительных элементов матрицы вектор.

Учащиеся затем решают, какие изменения нужно вносить, чтобы в задаче формировался вектор из всех элементов матрицы.

Контрольные вопросы:

1)Что такое матрица?
2) Что такое квадратная матрица?

3) Какое соответствие между индексами в выше и ниже диагонали, на диагонали?

Обработка строк и столбцов массива.

Задача 1. Среди нечетных столбцов данной це­лочисленной матрицы размерностью NXM (N< = 10, М<= 15) найти столбец с максимальной суммой модулей элементов.

Решение:

Var

A:array[1..10,1..15] of integer;

n,m,i,j,k:byte;

S,max: integer;

Begin

{Ввод размерности матрицы и элементов матрицы}

……………………..

{Максимальной суммой модулей элементов нечетных столбцов будем сначала считать сумму модулей эле­ментов первого столбца}

S:=0;

for i: = 1 to n do S: =S+ abs(A[i,l]);

max: =S;

k: = l;

j: = 3;

while j <=m do begin

S:=0;

for i: =1 to n do S: =S + abs(A[i,j];

if S>max then begin

max: =S;

k:=j

end;

j:=j + 2

end;

Writeln('Hoмep столбца с максимальной суммой мо­дулей элементов (',max,')-‘, k);

Readln;

End.

1. Дан двухмерный массив вещественных чисел размерностью m m, где m<=5. Найдите максимальный элемент на главной и на побочной диагоналях этого массива.

2. Среди строк данной целочисленной матрицы размерностью M N (N< = 10, М <= 15), содержащей только элементы, по своему абсолютному значению не превосходящие 10, найдите строку с мини­мальным произведением элементов.

3. Дана прямоугольная таблица В[1..5, 1..5]. Замените в ней стро­ки столбцами (первую строку — первым столбцом, вторую — вторым). Данный процесс называется транспонированием матрицы.

4. Сформируйте и выведите двухмерный целочисленный массив следующего вида:

а) 1 1 1 1 1 б) 5 5 5 5 5 в) 1 2 2 2 1 2 2 2 2 2 5 0 0 0 5 2 1 2 1 2 3 3 3 3 3 5 0 0 0 5 2 2 1 2 2 4 4 4 4 4 5 5 5 5 5 2 1 2 1 2 1 2 2 2 1

г) 1 2 3 4 5 д) 2 4 8 16 32 64 е) 2 4 6 8 10 12 14 2 3 4 5 6 4 4 0 0 0 0 3 4 6 8 10 12 14 3 4 5 6 7 8 0 8 0 0 0 5 15 6 8 10 12 14 4 5 6 7 8 16 0 0 16 0 0 7 17 25 8 10 12 14 5 6 7 8 9 32 0 0 0 32 0 9 19 27 33 10 12 14 64 0 0 0 0 64 11 21 29 35 39 12 14 13 23 31 37 41 43 14

5. 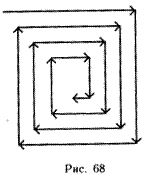Заполните матрицу размером v Х v,

где v < = 12, целыми числами 2, 4, 6, 8,

10 и т. д. по спирали (рис. 68).

6. Дана вещественная квадратная матрица размерностью 9X9. Найдите наибольшие элементы и их индексы в за­штрихованных областях (рис. 69, а, б).

14. Задана о древнем китайском квадрате. В древности китайцы использо­вали «магический» квадрат следующего вида (рис. 70). В обычной записи он не так эффектен:

4 9 2

3 5 7

8 1 6

Определите, является ли двухмерный массив из натуральных чисел N N, где 3< =N< =6, «магическим» китайским квадратом. «Маги­ческими» квадратами называются такие квадраты, в которых первые 9, 16, 25 и т. д. числа натурального ряда расположены в квадратной сетке таким образом, чтобы суммы чисел по строкам, столбцам и диагоналям оказались равными.

15. Рассмотрим «магический» китайский квадрат четвертого по­рядка (рис. 71). Составить алгоритм подсчета сумм элементов этого квадрата, которые расположены: а) по углам квадрата; б) в каждом из маленьких квадратов (по четыре клетки), которые примыкают к верши­нам данного квадрата; в) на противоположных сторонах вписанного квадрата (см. рис. 71). Какими дополнительными свойствами обладает «магический» квадрат четвертого порядка?

16. Задача о «магическом» квадрате произведения. «Магические» квадраты произведения содержат такие неповторяющиеся натуральные числа, что их произведения в каждой строке, в каждом столбце и на обеих диагоналях одинаковы. Постройте «магический» квадрат про­изведения 3-го порядка, созданный на основе двух простых чисел а = = 2, b = 3, следующего вида:

a²b 1 ab

b² ab a²

a a²b² b

17. Задача о латинском квадрате. Латинским квадратом называ­ется квадратная матрица из п чисел (или букв), такая, что каждое (каждая) из них встречается в каждой строке и каждом столбце только один раз. Например, латинский квадрат пятого порядка имеет вид:

1 2 3 4 5

2 3 4 5 1

3 4 5 1 2

4 5 1 2 3

5 1 2 3 4

Постройте алгоритм, определяющий, является ли квадратная матрица fXf, где f<=9, латинским квадратом.

18*. В ряду лежит N арбузов, пронумерованных от 1 до N, N '<=200. Известно, что массы первого и Л/-го арбузов М[1] и M[N] соответственно. Масса i-ro арбуза есть среднее арифметическое масс соседних арбузов, увеличенное на D: D + (M[i— 1]+ M [i+1])/2. Найди­те массу /-го арбуза.

19. Последовательность из нулей и единиц составлена по следую­щему правилу. Сначала вводится число А в двоичной системе счисле­ния (состоящее из нулей и единиц). Каждая цифра числа — это один элемент последовательности. Затем на каждом шаге к уже написанной части последовательности приписывается новая той же длины, получа­емая заменой всех нулей на единицы, а единиц на нули. Составьте алгоритм формирования и вывода данной последовательности, состоя­щей из N элементов. Например, А = 101, N = 3 (количество цифр числа А), полученная последовательность будет иметь вид 101010010101010101 101010.

Дата добавления: 2015-07-11