Рост популяции и кривые роста

Если при незначительной эмиграции и иммиграции рождаемость превышает смертность, то популяция будет рас­ти. Рост популяции является непрерывным процессом, если в ней существуют все возрастные группы. Скорость роста попу­ляции при отсутствии каких-либо экологических ограничений описывает дифференциальное уравнение:

dN/df= г N,

где N — численность особей в популяции; t — время; г — константа скорости естественного прироста.

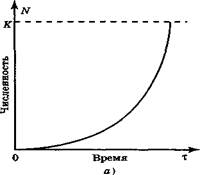
J -образная модель роста популяции (экспоненци­альная). Если г > 0, то со вре­менем численность популяции становится больше. Рост проис­ходит сначала медленно, а затем стремительно увеличивается по экспоненциальному закону, т. е. кривая роста популяции принимает J -образный вид (рис. 2, а). Такая модель осно­вывается на допущении, что рост популяции не зависит от ее плотности. Считают, что почти любой вид теоретиче­ски способен увеличить свою численность до заселения всей Земли при достатке пищи, воды, пространства, постоянстве условий среды и отсутствии хищников. Эта идея была выдви­нута еще на рубеже XVIII и XIX вв. английским экономистом Томасом Р. Мальтусом, основоположником теории мальтузи­анства.

Рис. 2. Типы кривых роста численности популяции (модели роста популяции): а — J образная; б — S-образная; К — поддерживающая емкость среды

S-образная модель роста популяции (логистическая) Иное развитие полу­чает ситуация при ограниченности пищевых ресурсов либо при скоплении токсичных продуктов (отходов) метаболизма. Первоначальный экспоненциальный рост в исходных благоп­риятных условиях со временем продолжаться не может и по­степенно замедляется. Плотность популяции регулирует ис­тощение пищевых ресурсов, накопление токсикантов и поэто­му влияет на рост численности. С увеличением плотности скорость роста популяции постепенно снижается до нуля, и кривая выходит на некоторый стабильный уровень (график об­разует плато). Кривая такого роста (рис. 2, б) имеет S-образную форму, и поэтому соответствующая модель развития со­бытий называется S-образной. Она характерна, например, для дрожжей, фактором, ограничивающим их рост, является на­копление спирта, а также для водорослей, самозатеняющих друг друга. В обоих случаях численность популяции не дости­гает уровня, на котором начинает сказываться нехватка эле­ментов питания (биогенов).

На рост численности, в которой значительную (возможно, даже главную) роль играет пространство, также влияет пере­населенность. Лабораторные опыты с крысами показали, что по достижении определенной плотности популяции плодови­тость животных резко снижается даже при избытке пищи. Возникают гормональные сдвиги, влияющие на половое по­ведение; чаще встречается бесплодие, поедание детенышей ро­дителями и т. п. Резко ослабевает родительская забота о по­томстве, детеныши раньше покидают гнездо, в результате чего снижается вероятность их выживания. Усиливается агрессив­ность животных. Подобные явления встречаются также в по­пуляциях ряда млекопитающих, причем не только в лабора­торных, но и природных условиях.

Скорость роста численности в S-образной модели определя­ет дифференциальное уравнение

dN/di = rN(1- N/K),

где К — поддерживающая емкость среды, т. е. максимальный размер популяции, которая может существовать в данных ус­ловиях, удовлетворяя свои потребности неопределенно долго.

Если N > К, скорость роста отрицательна. Если N < К, скорость роста положительна и величина популяции N стре­мится к К, т. е. приводится в соответствие с поддерживающей емкостью среды. Если N = К, скорость роста популяции равна нулю. При нулевом росте популяция стабильна, т. е. ее размеры не меняются, хотя отдельные организмы по-прежнему рас­тут, размножаются и отмирают. Происходящее размножение уравновешивается смертностью.

Поддерживающая емкость играет решающую роль не только при росте популяции по S-образной, но также и по J-образной модели, ибо в некоторый момент времени все же насту­пает исчерпание какого-либо ресурса среды, т. е. он (или даже несколько одновременно) становится лимитирующим. Разви­тие дальнейших событий показано на рис. 4.6, а, б. После бума с внезапным выходом J-образной кривой за пределы уровня К происходит крах популяции (модель типа «бум — крах»), т. е. катастрофа, приводящая к резкому снижению численности. Причиной краха часто быва­ет внезапное резкое изменение условий окружающей среды (экологических факторов), понижающее поддерживающую емкость среды. Тогда огромное число особей, не способных эмигрировать, погибает.

При наиболее благоприятном для популяции стечении об­стоятельств новый уровень численности соответствует поддер­живающей емкости среды или, иначе говоря, кривая роста превращается из J-образной в S-образную. Однако исчерпание пищевых ресурсов может привести также к появ­лению и других трудностей для популяции, например к разви­тию болезней. Тогда численность снижается до уровня значи­тельно более низкого, чем поддерживающая емкость среды, а в пределе популяция может даже быть обречена на вымирание.

Описанные модели роста популяции и дифференциальные уравнения предполагают, что все организмы сходны между со­бой, имеют равную вероятность погибнуть и равную способ­ность к размножению, так что скорость роста популяции в экс­поненциальной фазе зависит только от ее численности и не ог­раничена условиями среды, которые остаются постоянными. Они точно описывают процессы роста и взаимодействия особей в большинстве искусственных и некоторых естественных по­пуляциях. «Идеальность» всех экологических факторов в ис­ходных условиях предопределила то, что рассматриваемые мо­дели называют идеальными.

Для природных популяций принятые допущения чаще всего неверны. В естественных условиях J- и S-образные модели роста популяции преимущественно можно наблюдать в слу­чаях, когда тех или иных животных вселяют или они сами распространяются в новые для них районы. Тем не менее, те­оретические модели роста позволяют лучше понять процессы, происходящие в естественных условиях. Большинство прин­ципов, используемых для моделирования популяций живот­ных, применимо также и для моделирования популяций рас­тений.

Следует отметить, что при любой модели (как J-, так и S-образной) вначале характерна фаза экспоненциального роста численности популяции. Поэтому при сочета­нии благоприятных (оптимальных) значений всех факторов среды возникает «популяционный взрыв», т. е. особо быстрый рост популяции того или иного вида.

Дата добавления: 2015-07-11