Расчетная часть. 1. Преобразование гранулометрического состава.

1. Преобразование гранулометрического состава.

Т.к. гранулометрический состав определён достаточно грубо, для более точного расчета необходимо преобразовать состав. Допустим, что в пределах каждой фракции зависимость диаметра от его содержания линейная, построим график (см приложение 1), а по этому графику определим гранулометрический состав. Полученные данные сведём в таблицу 2.

Таблица 2 – Гранулометрический состав силикагеля.

Фракция, мм	0,25-0,45	0,45-0,75	0,75-1,02	1,02-1,22	1,22-1,39	1,39-1,55	1,55-1,67	1,67-1,79	1,79-1,90	1,90-2,00
Содержание, %

2. Определение среднего диаметра.

Цель: Рассчитать средний диаметр двумя методами и определить наиболее подходящий для нашего аппарата.

Для определения среднего диаметра необходимо определить средний диаметр фракции. Для определения среднего диаметра фракции существует несколько формул, выбор типа формулы зависит от типа распределения диаметра от содержания, основных формул 2: как среднее арифметическое и как среднее геометрическое

где d_ср – средний диаметр фракции, мм;

d_min – минимальный диаметр i-ой фракции, мм;

d_max – максимальный диаметр i-ой фракции, мм.

Для расчета параметров кипящего слоя необходимо знать так называемый средний диаметр, для определения которого существует две формулы

где d_ср – средний диаметр, мм;

d_ср,I – средний диаметр i-ой фракции, мм;

x_i – содержание фракции.

Определим средние диаметры фракций

По формуле (1) получаем:

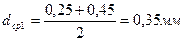
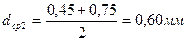
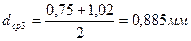
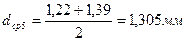
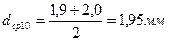
Находим средний диаметр:

1 метод:

2 метод:

Среднее значение диаметра частиц силикагеля:

d_СР=(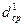 _.+ )/2=(0,975+1,287)/2=1,131мм

Вывод:

Так как слой зернистого материала состоит из частиц разных диаметров, нам нужно было определить средний диаметр частиц равный 1,131 мм. Нам будет, достаточно этого диаметра чтобы определить скорость псевдоожижения. Когда диаметр частицы маленький то достаточно и меньшей скорости, а если частица большого диаметра то нужна большая скорость псевдоожижения, мы берем среднее значения диаметров т.к. частички меньшего диаметра будут переходить в псевдоожиженное состояние, а частички большего размера будут, подцеплять и переводить частички меньшего размера.

3. Расчет порозности неподвижного слоя зернистого материала, e_н.с.

Цель: Рассчитать долю свободного объема в неподвижном слое зернистого материала.

Определяем параметры псевдоожижающего агента (воздуха) при температуре t=145 ⁰С:

Плотность рассчитывается по

,

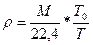
Где ρ – плотность, кг/м³;

М =29 – молярная масса воздуха, кг/кмоль;

Т₀ =273,15 – температура начала отсчета, К;

Т – температура среды, К.

Плотность воздуха равна:

По номограмме [2, стр 557, нов.] определяем вязкость воздуха:

μ = 0,024*10^-3 Па*с

где р_нас.= насыпная плотность, кг/м³

p_ч.= плотность частиц, кг/м³

р_р= плотность ожижающего агента, кг/м³

e_н.с.=

Вывод:

Мы рассчитали долю свободного пространства в неподвижном слое, ɛ_н.с.=0.409, что соответствует оптимальному значению (ɛ_н.с.=0,35-0,45). Порозность слоя является важной его характеристикой, так как он в значительной степени определяет на гидродинамику и интенсивность массо- и теплообмена в аппаратах с псевдоожиженным слоем зернистого материала.

4. Расчет скорости начала псевдоожижения w_кр1

Цель: Определить скорость начала "кипения" слоя зернистого материала.

Критерий Архимеда рассчитывается по формуле

Где Аr – критерий Архимеда;

d_экв – эквивалентный диаметр, м;

ρ_ч – кажущаяся плотность частиц, кг/м³;

ρ – плотность среды, кг/м³;

g =9,81 – ускорение свободного падения, м/с²;

μ – вязкость среды, Па*с.

Рассчитаем значение числа Архимеда для различных значений эквивалентного диаметра:

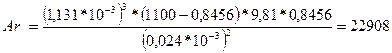
По данным значениям числа Архимеда находим первое критическое значение числа Рейнольдса по:

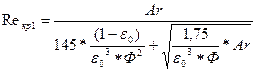
Где Re_кр1 – первое критическое значение числа Рейнольдса;

Ar – число Архимеда.

Рассчитаем первое критическое значение числа Рейнольдса:

По рассчитанному значению числа Рейнольдса рассчитывают значение первой критической скорости по формуле – начало псевдоожижения:

Где w_кр1 – первая критическая скорость, м/с;

μ – вязкость среды, Па*с;

Re_кр1 – первое критическое значение числа Рейнольдса;

d_экв – эквивалентный диаметр, м;

ρ – плотность среды, кг/м³.

Рассчитаем значения первой критической скорости для эквивалентного диаметра (средний диаметр берем):

м/с

Вывод:

При восходящем потоке газа (воздуха) через плотный слой зернистого материала с увеличением скорости потока увеличивается сопротивление слоя и ослабляется взаимное давление частиц. Когда скорость достигает 0,2848 м/с сопротивление слоя становится равным весу слоя, частицы перестают оказывать взаимное давление и слой переходит во взвешенное состояние.

5. Расчет второй критической скорости w_кр2

Цель: Определить предел существования взвешенного слоя.

Вторая критическая скорость (конец псевдоожижения) рассчитывается аналогично, в выражении для числа Архимеда и критической скорости вместо эквивалентного диаметра берётся минимальный. (d_min = 0.25 мм) Число Рейнольдса рассчитывают по:

Где Re_кр2 – второе критическое значение числа Рейнольдса;

Ar – число Архимеда для минимального диаметра.

Число Архимеда для минимального диаметра равно:

Число Рейнольдса равно

Вторая критическая скорость равна

м/с.

Вывод:

Практически пределом существования взвешенного слоя будет скорость, равная скорости витания данной частицы. В нашем аппарате это 1,0388 м/с. Если скорость будет выше, то псевдоожиженный слой прекращает свое существование.

---

Дата добавления: 2015-07-11