
|
Читайте также: |
В общем случае между моментом, развиваемым двигателем, и моментом сопротивления системы “электродвигатель – рабочая машина” существует соотношение, называемое уравнением движения электропривода:
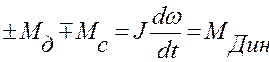 , (1.3)
, (1.3)
где 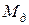 - момент, развиваемый двигателем;
- момент, развиваемый двигателем; 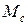 - момент сопротивления системы, приведенный к валу двигателя;
- момент сопротивления системы, приведенный к валу двигателя; 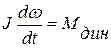 – динамический момент (
– динамический момент (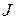 - момент инерции вращающихся частей системы “двигатель - рабочая машина“, приведенный к валу двигателя;
- момент инерции вращающихся частей системы “двигатель - рабочая машина“, приведенный к валу двигателя; 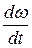 - угловое ускорение движущихся масс).
- угловое ускорение движущихся масс).
Уравнение (1.3) показывает, что развиваемый двигателем вращающий момент МД уравновешивается моментом сопротивления МС и динамическим моментом 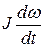 на его валу.
на его валу.
Когда момент, развиваемый двигателем, равен моменту сопротивления механизма, электропривод работает в установившемся режиме и скорость привода постоянна.
В случае ускорения или замедления привода возникает инерционная сила или инерционный момент, который двигатель должен преодолевать, работая в переходном режиме. Причиной возникновения переходных режимов в электроприводах является либо изменение нагрузки, связанное с производственным процессом, либо воздействие на электропривод при управлении им, т.е. пуск, торможение, изменение направления вращения и т.п.
Момент, развиваемый двигателем, принимается положительным, если он направлен в сторону движения привода, и отрицательным, если направлен в сторону, обратную движению (режим торможения).
Знак минус перед Мс указывает на тормозящее действие момента сопротивления, что соответствует силам нагрузки: резания, дробления, трения, сжатия, растяжения и т.п. В случае спуска груза, разжатия пружины и т.п. перед Мс ставят знак плюс, поскольку в этих случаях момент сопротивления помогает вращению привода.
Анализ уравнения (1.3) показывает следующее:
1) при М Д >Мс величина 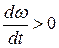 , и в этом случае имеет место ускорения привода;
, и в этом случае имеет место ускорения привода;
2) при МД< Мс величина 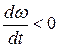 , т.е. имеет место замедление привода (очевидно, что замедление привода может быть и при отрицательном значении момента двигателя);
, т.е. имеет место замедление привода (очевидно, что замедление привода может быть и при отрицательном значении момента двигателя);
3) при Мд = Мс величина 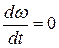 , в данном случае электропривод работает в установившемся режиме.
, в данном случае электропривод работает в установившемся режиме.
Аналогично (1.3) записывается уравнение движения электропривода для поступательного движения. При поступательном движении движущая сила Fд уравновешивается силой сопротивления рабочей машины Fс и инерционной силой 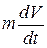 , возникающей при изменении скорости:
, возникающей при изменении скорости:
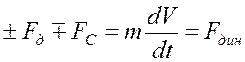 , (1.4)
, (1.4)
где Fд – усилие, развиваемое двигателем; Fс – приведенное усилие статических сопротивлений системы; m – приведенная масса движущихся частей системы; 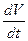 - линейное ускорение движущихся масс; Fдин – усилие динамических сопротивлений системы (силы инерции)
- линейное ускорение движущихся масс; Fдин – усилие динамических сопротивлений системы (силы инерции)
При практических расчетах моменты и масса различных элементов системы пересчитываются или приводятся к какому-либо одному из элементов, чаще всего к валу двигателя.
Основой для такого пересчета служит закон сохранения энергии:
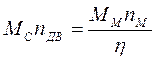 (1.5)
(1.5)
или
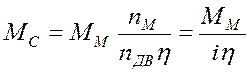 , (1.6)
, (1.6)
где МС – искомый момент статических сопротивлений, приведенный к валу двигателя; ММ – действительный момент статических сопротивлений машины; nДВ – скорость вращения двигателя; nМ – скорость вращения рабочей машины; η – к.п.д. передачи; i – передаточное число.
Обычно передаточные числа определяются как отношение скоростей вращения шкивов ведущего и ведомого в такой последовательности (по энергетическому потоку):
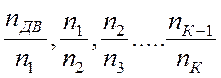 . (1.7)
. (1.7)
При наличии нескольких передач между двигателем и рабочей машиной момент сопротивления, приведенный к валу двигателя, определяется по выражению
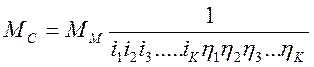 . (1.8)
. (1.8)
Если в системе имеются рабочие органы, совершающие поступательное движение с усилием FС и скоростью VМ, то это усилие может быть приведено к валу двигателя и заменено соответствующим моментом:
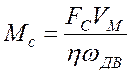 . (1.9)
. (1.9)
Определение приведенного момента инерции основано на равенстве энергий, запасенных при движении, с одной стороны, в фиктивном маховике, насаженном, например, на вал двигателя и обладающем приведенным моментом инерции JПР, с другой стороны – во всех движущихся звеньях системы, обладающих соответствующими моментами инерции J и массой m:
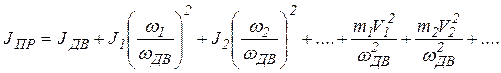 , (1.10)
, (1.10)
где ωДВ – угловая скорость вращения двигателя; ω1, ω2 – угловые скорости вращающихся частей рабочей машины; m1, m2, V1, V2 – соответственно массы и линейные скорости поступательно движущихся частей.
Пример 1.1. К схеме механической части электропривода (рис. 1.10) рассчитать значения приведенного момента инерции J и приведенного момента нагрузки Мс при подъеме груза. Дано: момент инерции двигателя вместе с муфтой М1 и шестерней Z1 JДВ =0,15 кг∙м2; момент инерции барабана вместе с муфтой М2 и шестерней Z2 JБ = 1,8 кг∙м2; КПД: редуктора ηР = 0,97, барабана ηБ = 0,95; угловая скорость двигателя ω = 93 рад/с, скорость подъема груза VП.Г. = 0,1 м/с; передаточное число редуктора iР = 6,14; масса груза вместе с крюком mг = 850 кг.
Решение. Определяем приведенный момент нагрузки МС по формуле
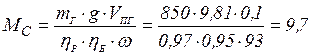 Н∙м,
Н∙м,
где g = 9,81 м/с2 – ускорение силы тяжести;
m∙g = FС – усилие поступательного движения.
Находим приведенный момент инерции J по выражению
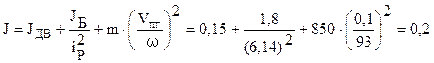 кг∙м2.
кг∙м2.
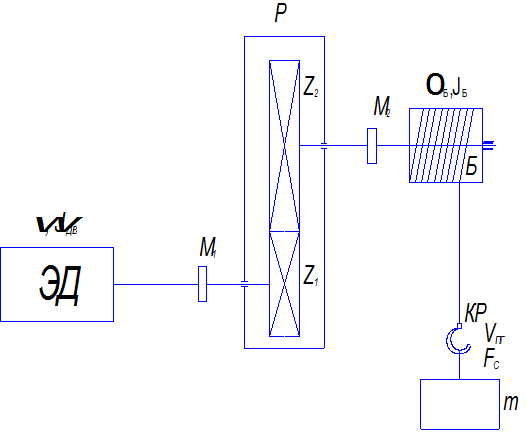
Рис. 1.10. Схема механической части электропривода подъемной лебедки
Пример 1.2. У молочного сепаратора определить приведенные к валу двигателя: момент инерции J сепаратора с электроприводом и момент сопротивления барабана МС, который в теории электропривода называют статическим моментом. Передача клиноременная и червячная. Данные электродвигателя: диаметр ротора D1 = 0,1 м, масса ротора m1=4,5 кг, скорость n1 = 1400 об/мин. Данные молочного сепаратора: диаметр барабана D2 = 0,14 м, масса барабана m2 = 4 кг, скорость n2 = 8000 об/мин, момент сопротивления барабана МБ = 2,2 Н∙м.
Решение. Момент инерции барабана сепаратора и ротора электродвигателя вычислим по выражению
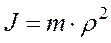 ,
,
где m – масса вращающегося тела, кг; ρ – радиус инерции вращающегося тела, зависящий от формы этого тела, м.
Принимаем ротор электродвигателя и барабан сепаратора за сплошные цилиндрические тела. Радиус инерции сплошного цилиндрического тела определяется по формуле
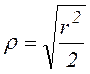 ,
,
где r – радиус цилиндрического тела, м.
Определяем момент инерции ротора:
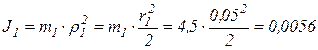 кг∙м2,
кг∙м2,
где 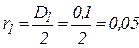 м.
м.
Находим момент инерции барабана:
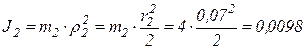 кг∙м2,
кг∙м2,
где 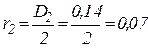 м.
м.
Приведенный момент инерции сепаратора с электроприводом
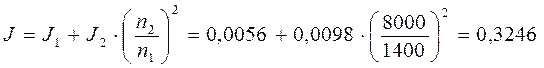 кг∙м2.
кг∙м2.
Приведенный момент сопротивления барабана сепаратора
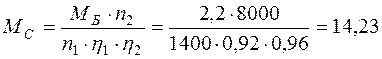 Н∙м,
Н∙м,
где η1 = 0,92 – КПД клиноременной передачи;
η2 = 0,96 – КПД червячной передачи.
Контрольные вопросы
1. Что такое электропривод?
2. Из каких основных частей состоит электропривод?
3. Какую зависимость выражает механическая характеристика производственной машины?
4. Приведите типовые механические характеристики рабочих машин (транспортера, нории, центробежного насоса).
5. Какие величины входят в уравнение движения электропривода при вращательном и поступательном движении?
[1] ГОЭЛРО – Государственная комиссия по электрификации России (БСЭ., 1952 г.)
Дата добавления: 2015-07-11; просмотров: 139 | Нарушение авторских прав