Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Решение. 1. Найти усилия в тягах, реакции в опоре С и угловое смещение (поворот бруса вокруг т

⇐ ПредыдущаяСтр 7 из 7


Читайте также:
  1. Берлин принимает решение
  2. БЛОК МЕТОДИК, СВЯЗАННЫХ С РЕШЕНИЕМ ЧЕЛОВЕКОМ ЖИЗНЕННЫХ ПРОБЛЕМ
  3. Ваше решение
  4. Ваше сегодняшнее решение относительно семьи
  5. Внесение изменений в решение о выпуске
  6. Внесение изменений в решение о выпуске и/или проспект российских депозитарных расписок
  7. Возможность заказчика принять решение об одностороннем отказе от исполнения контракта в соответствии с гражданским законодательством.

 

1. Найти усилия в тягах, реакции в опоре С и угловое смещение (поворот бруса вокруг т. С), как функции от величины силы Р. Для определения величин усилий в тягах в зависимости от Р применим метод сечений. Сделав сечение по всем тягам и приложив в местах сечений усилия N 1, N 2 и N 3, возникающие в тягах, рассмотрим равновесие остав­шейся части, нагруженной продольными усилиями в тягах N 1, N 2 и N 3 реакциями опоры С (RC и HC) и силой Р (рис. 2.12, б). Составив уравнения равновесия статики для оставшейся части, получим:

1) S z = 0, НC = 0; (2.29)

2) S y = 0, - Р + N 1 + RC - N 2 - N 3 = 0; (2.30)

3) S MC = 0, - Р ×3 + N 1×1 + N 2×1 + N 3×3 = 0. (2.31)

Рис. 2.12

Из уравнений равновесия видно, что система дважды стати­чески неопределима, т.к. два уравнения равновесия (2.30) и (2.31) содержат в своем составе четыре неизвестных. Поэтому для реше­ния задачи необходимо составить два дополнительных уравнения совместности деформаций, раскрывающих статическую неопреде­лимость системы.

Для составления дополнительных уравнений рассмотрим де­формированное состояние системы (рис. 2.12, в), имея в виду, что брус абсолютно жесткий и поэтому после деформации тяг останет­ся прямолинейным.

Эти дополнительные уравнения совместности деформаций по­лучим из подобия треугольников ВСВ 1~ DCD 1 и BCB 1~ ECE 1:

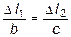и .

Решая эти уравнения, получим:

(2.32)

. (2.33)

Выразив деформации тяг по формуле определения абсолютного удлинения:

и подставив эти значения в уравнения (2.32) и (2.33), получим:

(2.34)

. (2.35)

Подставив найденные значения N 2 и N 3 в уравнение (2.31) оп­ределяем величину N 1 :

- P ×3 + N 1×1 + 0,5× N 1×1 + 2,5× N 1×3 = 0; N 1=0,3333 P.

Зная N 1, из уравнений (2.34) и (2.35), находим N 2 и N 3:

.

Опорную реакцию RC определяем из уравнения (2.30), подста­вив найденные значения N 1, N 2 и N 3:

-P + 0,333 P + RC - 0,167 P - 0,833 P = 0; RC = 1,667 P.

После определения величин усилий в тягах N 1, N 2, N 3 и реак­ции RC необходимо проверить правильность их вычисления. Для этого составим уравнение равновесия статики S МA = 0:

- N 1× a - RC (a + b) + N 2 (a + b + c) + N 3 (a + b + c + d) = 0;

0 = 0.

Следовательно, N 1, N 2, N 3 и RC определены правиль­но.

Угловое смещение бруса (угол j), ввиду его малости, находим как тангенс угла наклона бруса АЕ:

[рад].

2. Определить в процессе увеличения нагрузки Р такую ее величину, при которой напряжение в одной из тяг достигнет предела текучести. Для вы­числения величины Р, при которой напряжение в одной из тяг достигнет предела текучести s T, определим нормальные напряже­ния, возникающие в тягах, учитывая то, что тяги работают на рас­тяжение:

Полученные величины напряжений показывают, что в тяге 3 напряжение достигнет предела текучести раньше, чем в тягах 1 и 2, так как s3 > s1 и s3 > s2. Поэтому, приравняв напряжение s3 пре­делу текучести s T, определим величину Р, при которой нормальное напряжение в тяге 3 достигнет предела текучести s T:

кПа,

откуда

кН.

 

 

Вопросы для самопроверки

 

 

Дата добавления: 2015-07-11; просмотров: 60 | Нарушение авторских прав

⇐ Предыдущая1234567



mybiblioteka.su - 2015-2024 год. (0.007 сек.)