Лекция 6. Кривые второго порядка

Эллипс, парабола и гипербола как геометрические места точек плоскости. Канонические уравнения. Единый геометрический подход к определению эллипса, параболы и гиперболы. Полярные уравнения.

Определение 6.1. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости и , называемых фокусами, есть величина постоянная (рис.1).

Рис. 1. Эллипс

Расстояние между фокусами обозначим , сумму расстояний от произвольной точки эллипса до фокусов – . Расположим систему координат так, чтобы фокусы эллипса находились в точках и . Произвольная точка эллипса 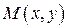удовлетворяет условию , т. е.

.

Преобразуем уравнение:

,

,

,

,

,

.

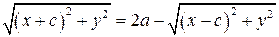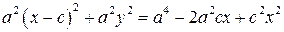Обозначим , тогда уравнение эллипса примет следующий вид:

.

Определение 6.2. Уравнение эллипса вида

называется каноническим уравнением эллипса.

Определение 6.3. Точки, в которых эллипс пересекает оси, называются вершинами этого эллипса.

Координаты вершин: , .

Определение 6.4. Число называют большой полуосью, а – малой полуосью эллипса.

Обычно предполагается . При условии получим уравнение окружности . Если , то фокусы эллипса расположены на оси ординат.

Определение 6.5. Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси,

.

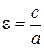Эксцентриситет эллипса удовлетворяет условию , причем в случае, когда эксцентриситет равен нулю, имеем окружность.

Определение 6.6. Гиперболой называется множество всех точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух данных точек той же плоскости и , называемых фокусами, есть величина постоянная (рис. 2).

Расстояние между фокусами обозначим , разность расстояний от произвольной точки эллипса до фокусов – . Расположим систему координат так, чтобы фокусы эллипса находились в точках и . Произвольная точка гиперболы удовлетворяет условию , то есть

.

Рис. 2. Гипербола

После преобразований уравнение гиперболы примет следующий вид:

.

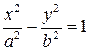Определение 6.7. Уравнение гиперболы вида

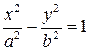
называется каноническим уравнением гиперболы.

Здесь .

Определение 6.8. Величины и называются, соответственно, действительной и мнимой полуосями гиперболы.

Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат.

Определение 6.9. Точки называются вершинами гиперболы.

Гипербола имеет две асимптоты:

, .

Определение 6.10. Гипербола называется равносторонней, если .

Уравнение равносторонней гиперболы имеет вид

,

асимптоты равносторонней гиперболы .

Определение 6.11. Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси

.

Эксцентриситет гиперболы больше единицы, , причем эксцентриситет равносторонней гиперболы равен

.

Определение 6.12. Параболой называется множество всех точек плоскости, для каждой из которых расстояние до точки , называемой фокусом, равно расстоянию до данной прямой , называемой директрисой, не проходящей через точку (рис.3).

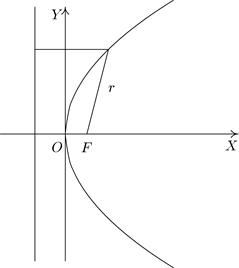
Рис. 3. Парабола

Если выбрать систему координат так, чтобы директрисой параболы была прямая , а фокусом точка , то уравнение параболы примет вид

.

Определение 6.13. Уравнение параболы вида

называться каноническим уравнением параболы.

Уравнение задает параболу, симметричную относительно оси ординат. При ветви параболы обращены в положительную сторону соответствующей оси, а при – в отрицательную.

Эксцентриситет параболы считается равным единице, .

Эллипсу и гиперболе можно поставить в соответствие две прямые, заданные уравнениями

, .

Эти прямые называются директрисами эллипса либо гиперболы, они симметричны относительно оси ординат. Эллипс, гипербола и парабола обладают следующим свойством.

Теорема 6.1. Если – произвольная точка эллипса (рис.4), гиперболы (рис.5) либо параболы, то отношение расстояние от до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету.

Рис. 4. Геометрические характеристики эллипса

Рис. 5. Геометрические характеристики параболы

Зададим эллипс, гиперболу и параболу уравнениями в полярных координатах. Легко проверить следующие результаты.

Лемма 6.2. Расстояние от произвольной точки 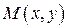, лежащей на эллипсе, до каждого из фокусов является линейной функцией от ее абсциссы :

, .

Лемма 6.3. Расстояние от произвольной точки 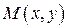, лежащей на гиперболе, до каждого из фокусов зависит от ее абсциссы следующим образом: для правой ветви гиперболы

, ,

для левой ветви

, .

Рассмотрим эллипс. Поместим начало полярной системы координат в левый фокус, направление полярной оси выберем совпадающим с направлением оси абсцисс. Тогда абсцисса произвольной точки определяется равенством

,

где – полярный радиус и – полярный угол. Из леммы 6.2 следует, что расстояние от точки эллипса до левого фокуса равно

,

отсюда . Таким образом, полярное уравнение эллипса имеет вид

.

Составим полярное уравнение гиперболы. Полюс поместим в правый фокус гиперболы. Для точек правой ветви гиперболы справедливы равенства и , откуда получим

.

Определение 6.14. Величина называется фокальным параметром эллипса или гиперболы.

Подставляя значение фокального параметра, запишем полярные уравнения эллипса и гиперболы в одном и том же виде:

.

Рассмотрим параболу. Поместим начало полярной системы координат в фокус параболы, полярную ось направим в положительную сторону оси абсцисс. Тогда для любой точки параболы расстояние до полюса равно расстоянию до директрисы . Так как , то уравнение параболы в полярных координатах записывается так же, как для эллипса и гиперболы:

,

при условии .

Вопросы для самопроверки

1. Как геометрически определяются эллипс, парабола и гипербола?

2. Напишите канонические уравнения эллипса, параболы и гиперболы.

3. Что называется эксцентриситетом эллипса, параболы и гиперболы?

4. Каковы уравнения эллипса, параболы и гиперболы в полярных координатах?

5. Какие прямые называются директрисами эллипса, параболы и гиперболы?

6. Как изменяется форма эллипса и гиперболы в зависимости от изменения их эксцентриситетов?

Дата добавления: 2015-07-11