
|
Читайте также: |
Материалом конструкции выбираем нержавеющую сталь, коэффициент теплопроводности стали λ=17,5 Вт/(м·К) (таблица XXVIII [1]).
Коэффициент теплопередачи в корпусе рассчитывается по формуле
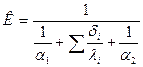 ,
,
где α1 – коэффициент теплоотдачи от греющего пара к стенке tст1;
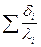 – сумма термического сопротивления стенки и загрязнений;
– сумма термического сопротивления стенки и загрязнений;
α2 – коэффициент теплоотдачи от стенки tст2 к кипящему раствору.
Принимаем, что суммарное термическое сопротивление равно термическому сопротивлению стенки δст/λст и накипи δн/λн. Термическое сопротивление загрязнений со стороны пара не учитываем.

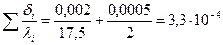 (м2·К)/Вт.
(м2·К)/Вт.
Коэффициент теплоотдачи от конденсирующего пара к стенке α1 равен
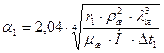 ,
,
 где r1 – удельная теплота конденсации греющего пара(таблица LVII [1]), r1=2186,5 кДж/кг;
где r1 – удельная теплота конденсации греющего пара(таблица LVII [1]), r1=2186,5 кДж/кг;
ρж – плотность конденсата, ρж=937 кг/м3;
λж – теплопроводность конденсата, λж=0,686 Вт/(м·К);
μж – коэффициент динамической вязкости конденсата, (таблица XXXIХ [1]), μж=216,75·10-6 Па·с;
Δt1 – разность температур конденсации пара и стенки, Δt1=2 °С;
Н – высота кипятильных труб, зависящая от Fор;
Fор – ориентировочная поверхность теплопередачи выпарного аппарата, которая определяется по формуле
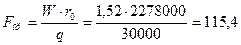 м2,
м2,
где q=30000 Вт/м – удельная тепловая нагрузка для аппарата с принудительной циркуляцией.
По ГОСТ 11987 – 81 для выпарного аппарата с принудительной циркуляцией и вынесенной греющей камерой выбираем: F=125 м2, dн=38∙2 мм – диаметр трубы, Н=6 м – высота трубы.
На основании всех определенных значений рассчитываем коэффициент теплоотдачи α1 по формуле
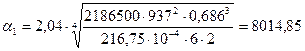 Вт/(м2·К).
Вт/(м2·К).
Определяем физические, теплофизические свойства растворов. Плотность раствора KCl при конечной концентрации 26 % принимаем ρ=1143 кг/м3. На основании правила линейности константа уравнения равна
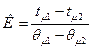 ,
,
где tμ1, tμ2 – температуры жидкости при вязкости раствора μ1 и μ2;
θμ1, θμ2 – температуры эталонного вещества при вязкости раствора μ1 и μ2.
Для раствора KCl:
– при t1=20 °С μ1=1,04 мПа·с (таблица VIII [1]);
– при t2=30 °С μ2=0,87 мПа·с.
В качестве эталонного вещества используем глицерин:
– при μ1=1,04 мПа·с θμ1=82 °С (рисунок V [1]);
– при μ1=0,87 мПа·с θμ2=88 °С.
Определяем константу уравнения К
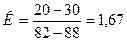 .
.
Константу К можно записать следующим образом
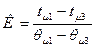 ,
,
где tμ1=20 °С, tμ3= tк.р.=98,62 °С;
θμ1=82 °С, θμ3 – температура глицерина, при которой вязкость равна μ3:

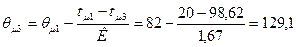 °С,
°С,
Для глицерина μ3=0,34 мПа·с, при θμ3=129,1 °С (рисунок V [1]);
Таким образом, динамический коэффициент вязкости KCl при tк.р.=98,62 °С равен μ=0,34 мПа·с.
Определяем удельную теплоемкость 26 % раствора KCl при tк.р.=98,62 °С по формуле
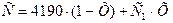 ,
,
где С1 – удельная теплоемкость безводного растворенного вещества, которая определяется по формуле:
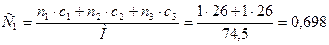 Дж/(кг·К),
Дж/(кг·К),
где М – молекулярная масса KCl;
n1, n2, n3 – число атомов элементов, входящих в соединение;
с1, с2, с3 – атомные теплоемкости, Дж/(кг-атом·К) (таблица 5.1 [1]).
Определяем удельную теплоемкость 26 % раствора KCl
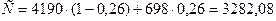 Дж/(кг·К).
Дж/(кг·К).
Определяем коэффициент теплопроводности 26 % раствора KCl при tк.р.=98,62 °С по формуле
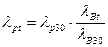 ,
,
где λвt – коэффициент теплопроводности воды при tк.р., λвt=0,675 Вт/(м·К);
λв30 – коэффициент теплопроводности воды при t=30 °С (рисунок Х [1]), λв30=0,616 Вт/(м·К);
λр30 – коэффициент теплопроводности 26 % раствора KCl при t=30 °С, определяется по формуле
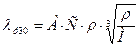 ,
,
где А – коэффициент, зависящий от степени ассоциации жидкости, А=3,58·10-8 м3·кмоль-1/3·с-1;
ρ=1143кг/м3 – плотность раствора;
М – мольная масса раствора, которая рассчитывается по формуле
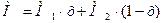 ,
,
где х – мольная масса твердой фазы, которая рассчитывается по формуле
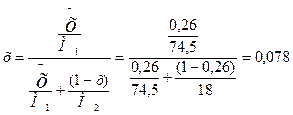 ;
;
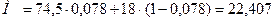 кг/кмоль.
кг/кмоль.
Определяем коэффициент теплопроводности 26 % раствора KCl при t=30 °С
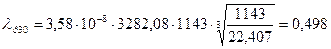 Вт/(м·К).
Вт/(м·К).
Тогда коэффициент теплопроводности раствора равен
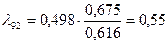 Вт/(м·К).
Вт/(м·К).
Определяем коэффициент теплоотдачи α2 по формуле
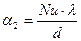 ,
,
где Nu – критерий Нуссельта, для аппаратов с принудительной циркуляцией определяется по формуле
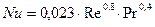 ,
,
где Re – критерий Рейнольдса;
Pr – критерий Прандтля.
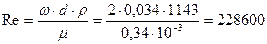 ,
,
где ω=2 м/с – скорость раствора (таблица 1.1 [1]).
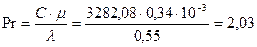 .
.
Подставляем полученные значения в формулу
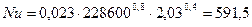
По полученным значениям находим коэффициент теплоотдачи
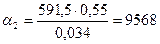 Вт/(м2·К).
Вт/(м2·К).
По полученным значениям α1 и α2 определяем коэффициент теплопередачи
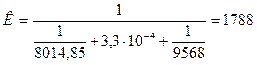
 1.4 Характеристики выпарного аппарата
1.4 Характеристики выпарного аппарата
Рассчитываем поверхность теплопередачи выпарного аппарата
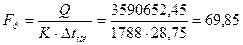 м2.
м2.
Принимаем выпарной аппарат со следующими параметрами: поверхность теплопередачи F=100 м2; диаметр греющей камеры D=800 мм; диаметр сепаратора D1=1800 мм; диаметр циркуляционной трубы D2=500 мм; высота аппарата Н=21500 мм; масса аппарата М=14500 кг.
Диаметр штуцера, через который поступает греющий пар
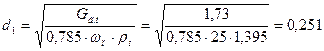 м,
м,
где Gг.п.=1,73 кг/с;
ωп=25 м/с – скорость греющего пара (таблица 1.1 [1]);
 ρп=1,395 кг/м3 – плотность пара при tг.п.=127,37 ºС (таблица LVI [1]).
ρп=1,395 кг/м3 – плотность пара при tг.п.=127,37 ºС (таблица LVI [1]).
Принимаем диаметр d1=273х10 мм (приложение А1 [2]).
Диаметр штуцера, через который выходит конденсат
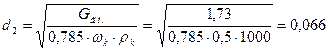 м,
м,
где Gг.п.=1,73 кг/с;
ωк=0,5 м/с – скорость конденсата (таблица 1.1 [1]);
ρк=1000 кг/м3 – плотность конденсата (таблица ХХХIХ [1]).
Принимаем диаметр d2=70х3 мм (приложение А1 [2]).
Диаметр штуцера, через который выходит вторичный пар
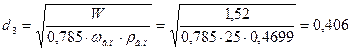 м,
м,
где W=1,52 кг/с;
ωв.п=25 м/с – скорость вторичного пара (таблица 1.1 [1]);
ρв.п=0,4699 кг/м3 – плотность вторичного пара (таблица LVI [1]).
Принимаем диаметр d3=426х11 мм (приложение А1 [2]).
Диаметр штуцера, через который поступает раствор
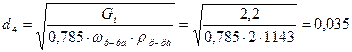 м,
м,
где Gн=2,2 кг/с;
ωр-ра=2 м/с – скорость поступающего раствора (таблица 1.1 [1]);
ρр-ра=1143 кг/м3 – плотность раствора.
Принимаем диаметр d4=38х2 мм (приложение А1 [2]).
Диаметр штуцера, через который выходит упаренный раствор
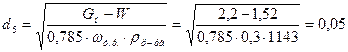 м,
м,
где Gн=2,2 кг/с;
W=1,52 кг/с;
ωу.р.=0,3 м/с – скорость упаренного раствора (таблица 1.1 [1]);
ρр-ра=1143 кг/м3 – плотность раствора.
Принимаем диаметр d3=56х3,5 мм (приложение А1 [2]).
Дата добавления: 2015-07-10; просмотров: 262 | Нарушение авторских прав