Растяжение-сжатие.

Растяжением (сжатием) стержня называется такое напряженное состояние, при котором в любом его поперечном сечении все внутренние силы, распределенные равномерно по всему сечению, приводятся к равнодействующей осевой силе N, называемой продольной силой.

Применяя метод сечений, т. е. рассматривая равновесие любой отсеченной части стержня под действием внешних нагрузок и внутренней осевой силы N, получим, что продольная сила N равна алгебраической сумме проекций всех внешних нагрузок, находящихся по одну сторону сечения, на ось стержня.

При растяжении-сжатии, в поперечных сечениях стержня возникают нормальные напряжения, которые определяются по формуле:

(2.1)

Условия прочности имеет вид:

(2.2)

здесь N – продольная сила,

F – площадь поперечного сечения,

- допускаемое напряжение материала стержня,

s_о – опасные напряжения материала (равные пределу текучести для пластичного материала и пределу прочности – для хрупкого),

n_о – основной коэффициент запаса прочности.

Из условия прочности (2.2) можно вычислить необходимую площадь поперечного сечения стержня:

или определить допускаемую нагрузку:

или проверить надежность конструкции.

Абсолютная величина деформации участка стержня при постоянной продольной силе, действующей на этом участке, и известной площади поперечного сечения определяется по закону Гука:

; (2.3)

где Е – модуль продольной упругости или модуль Юнга.

При действии на некотором участке стержня продольной равномерно распределенной нагрузки интенсивностью q продольная сила определяется следующим образом:

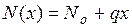, (2.4)

где N_о – продольная сила в начале участка.

В этом случае напряжения можно вычислить по формуле:

. (2.5)

Деформации только от распределенной нагрузки равны:

. (2.6)

С учетом всех нагрузок деформацию участка стержня длиной L проще всего определять по формуле:

, (2.7)

где N_ср – средняя величина продольной силы на участке с распределенной нагрузкой.

Если у системы (конструкции) число связей (следовательно, реакций связей) больше чем число уравнений статики, то такие системы называются статически неопределимыми. По числу «лишних» связей определяют степень статической неопределимости системы. Для составления недостающих уравнений, исходя из условий совместимости деформаций, рассматривают геометрическую сторону задачи и находят связь между деформациями элементов конструкции. Выражая деформации в соответствии с законом Гука через усилия, получим недостающие уравнения.

Пример №1. Представленный на рис. 2.1 ступенчатый стержень нагружен системой внешних нагрузок. Требуется построить эпюры продольных сил, нормальных напряжений и перемещений.

Рисунок 2.1

Решение.

Определяем на участках стержня значения продольных сил:

N_1-2 = Р₁ = 20 кН;

N_2-3 = Р₁ – Р₂ = 20 – 10 = 10 кН;

N_3-4 = Р₁ – Р₂ = 10 кН;

N_4-5 = Р₁ – Р₂ – qх,

при х = 0 Þ N₄ = Р₁ – Р₂ = 10 кН.

при х = 2м Þ кН.

.

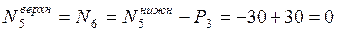Эпюра продольных сил приведена на рис. 2.2. Находим на каждом участке величины напряжений:

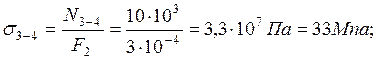
Эпюра нормальных напряжений показана на рис. 2.2.

Рисунок 2.2.

Эпюра перемещений строится со стороны закрепленного конца, т. к. защемленное сечение неподвижно т. е. d₆ = 0. Далее определяем перемещения соответствующих точек стержня:

т. к. N_5-6 = 0, получим

,

м.

На участке 4-5 эпюра перемещений имеет экстремум в сечении Х_о, где продольная сила равна нулю. Найдем значение Х_о из условия:

N(х_о) = - 30 + qх_о = 0, Þ м

и тогда экстремальное значение перемещения на этом участке будет:

м.

Определяем перемещение сечения «3», которое равно деформации участка 6-3, при известных деформациях участков 5-6 и 4-5:

м.

Аналогично определяем:

м.

м.

Эпюра перемещений представлена на рис. 2.2.

Анализ эпюр показывает, что сосредоточенные силы вызывают скачки в эпюрах «N» и «s», а в эпюре «d» - излом. На участках с распределенной нагрузкой эпюры «N» и «s» переменны, а эпюра «d» изменяется по параболическому закону. Резкое изменение поперечного сечения вызывает скачок на эпюре «s» (сечение «3»).

Пример №2. Ступенчатый брус защемлен обоими концами и нагружен системой внешних нагрузок, как показано на рис. 2.3. Материал бруса сталь Ст.3 с пределом текучести s_т = 240 МПа и основным коэффициентом запаса прочности п _т = 1,5.

Модуль упругости Е = 2* 10⁵ Мпа. Площадь сечения принять F = 4 см².

Требуется:

Построить эпюру «N» в долях «Р»;

Построить эпюру «s» в долях «Р/ F»;

Определить из условия прочности допускаемую нагрузку [Р];

При данной нагрузке [Р] построить эпюру перемещений «d».

Рисунок 2.3.

Решение.

Из уравнений равновесия определим реакции опор (рис. 2.4а).

Имеем систему сходящихся сил, для которой уравнение равновесия имеет вид:

Т. е. одно уравнение статики с двумя неизвестными R₁ и R₂. Система один раз статически неопределима.

а) б) в) г) д)

Рисунок 2.4.

Рассмотрим геометрическую сторону задачи. Поскольку опорные сечения неподвижны, их взаимное перемещение равно нулю, т. е.

;

Освободим один конец стержня (верхний) как показано на рис. 2.4б. В соответствии с принципом независимости действия сил, взаимное перемещение определяется как сумма деформаций от действующих на стержень нагрузок:

;

Запишем последнее выражение, заменив каждую составляющую с помощью закона Гука:

.

Умножив обе части этого уравнения на и подставив значения усилий Р₁ = Р и Р₂ = 3Р, получим:

,

откуда .

Знак «минус» указывает на то, что R₁ направлена в противоположную сторону. На рис. 2.4 старое направление R₁ зачеркнуто, а действительно направленная вниз реакция .

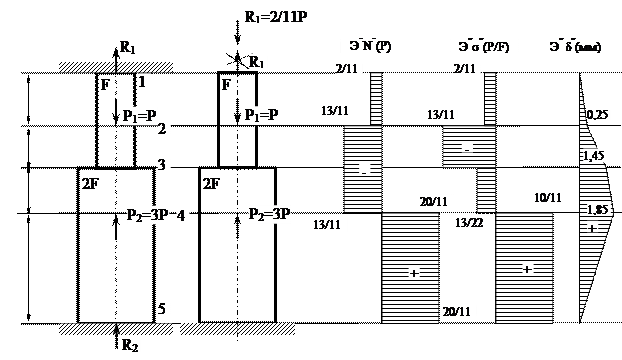
Построим эпюру «N» в долях «Р» (рис. 2.4в), для чего запишем выражения продольной силы на каждом участке стержня:

N_1-2 = -R₁ =-2/11P;

N_2-3 = -R₁ – Р₁ = – 13/11P;

N_3-4 = -R₁ – Р₁ = -13/11P;

N_4-5 = -R₁ - Р₁ + Р₂ = -13/11P + 3P = 20/11P.

Учитывая площади поперечных сечений каждого участка находим напряжения и строим эпюру нормальных напряжений в долях Р/ F (рис. 2.4г):

.

Очевидно, что наибольшее напряжение

Запишем условие прочности:

,

где .

Тогда

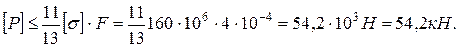
Построим эпюру перемещений, определив смещения в характерных точках стержня.

,

м;

м;

м;

м.

Как видно из результатов расчета, перемещения в защемленных сечениях 1 и 5 равны нулю, что подтверждает правильность решения. Эпюра перемещений показана на рис. 2.4д.

Пример №3. Абсолютно жесткий брус ОВ закреплен шарнирно в точке О, подпоркой АС и тягой ВД. Брус нагружен силой Р = 100 кН. Материал подпорки и тяги – сталь Ст. 4 с пределом текучести s_т =300 Мпа. Определить площади поперечного сечения подпорки и тяги – F₁ и F₂, если F₁/ F₂ = ½. В расчетах принять коэффициент запаса прочности n_т = 1,5.

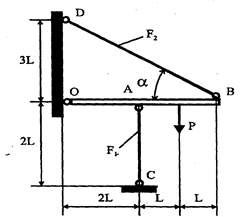
Рисунок 2.5.

Решение.

Составим план предполагаемых усилий (рис. 2.6).

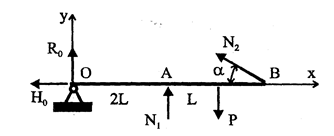
Рисунок 2.6.

Запишем уравнение равновесия системы:

.

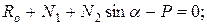
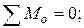
В результате получим три уравнения статики с четырьмя неизвестными R_о, H_о, N₁ и N₂. Т. е. система один раз статически неопределима.

Для раскрытия статической неопределимости построим план предполагаемых перемещений (рис. 2.7).

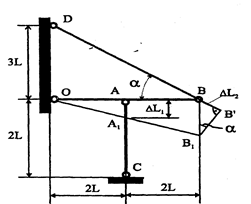
Рисунок 2.7.

Под действием силы Р жесткий брус ОАВ повернется вокруг точки О, при этом точки А и В соответственно займут положение А₁ и В₁. Из подобия треугольников ОАА₁ и ОВВ₁ имеем:

, где .

В треугольнике ВВ₁В¢ угол 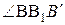=α, т. к. ВВ₁ ^ ОВ, а В₁В¢ ^ ДВ, поэтому . Подставив и ВВ₁ в пропорцию, получим условие совместимости деформаций в виде:

.

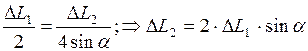Выражаем и в соответствии с законом Гука через усилия, действующие в стержнях:

здесь:

; ,

Учитывая, что 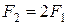, получим после подстановки:

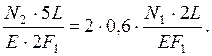
После упрощения этого выражения получим недостающее уравнение в виде:

Решаем совместно с этим уравнением третье уравнение равновесия и учитывая, что

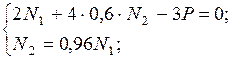
получим величины усилий:

кН; кН.

Определим площади поперечных сечений стержней. Для этого сначала найдем допускаемое напряжение:

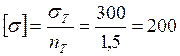Мпа.

Записываем условие прочности для подпорки АС и определяем площадь поперечного сечения:

;

.

Из соотношения площадей находим:

см².

Далее из условия прочности для тяги АС проверяется правильность определения площади . В случае, если условие прочности не удовлетворяется, необходимо сначала определить , а затем из соотношения площадей найти новое значение площади .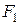

Проверим прочность стержня ВД:

.

Таким образом, прочность конструкции обеспечена.

Дата добавления: 2015-07-10