Классификация ПИ по характеру их проявления

Традиционным является деление погрешностей на случайные, систематические и грубые, и этот же подход принят в стандартах.

Процесс измерения характеризуется фактическим наличием как детерминированных, так и случайных (стохастических) явлений, которые вызывают появлениесоответствующих погрешностей. Так наряду с закономерным изменением длины стержня при повышении или понижении температуры широко известно броуновское движение, которое следует рассматривать как проявление стохастических (случайных) явлений, проходящих на молекулярном уровне. Объединенные воздействия множества явлений, из-за неопределенности действующих факторов, малости воздействия каждого из них и неоднозначности объединения воздействий отдельных факторов, в итоге приводят к появлению случайных результатов.

С другой стороны, очевидно наличие погрешностей с детерминиро-ванным механизмом образования. И средства измерений, и измеряемые объекты, и окружающая среда подчиняются физическим законам. Поэтому приходится считаться с широтой и высотой над уровнем моря места взвешивания объекта на пружинных весах, с увеличением объема тел при нагревании, с диэлектрическими свойствами воздуха при использовании емкостных преобразователей и с его оптическими свойствами при измерении длины лазерным интерферометром.

3.1. Систематическая погрешность – составляющая погрешности результата измерения, закономерно изменяющаяся при повторных измерениях одной и той же физической величины.

К систематическим погрешностям измерений относятся те составляю-щие, для которых доказано наличие функциональных связей с вызываю-щими их аргументами. Формально это записывается в виде

D_s = F (j, y...),

где j, y – аргументы, вызывающие систематическую погрешность.

Например, неправильная настройка прибора («сбитый ноль») приводит к появлению постоянной составляющей погрешности при любых измерениях, проводимых до изменения настройки.

Главной особенностью систематической погрешности является принципиальная возможность ее выявления, прогнозирования и однозначной оценки, если удается узнать вид функции и значения аргументов.

В зависимости от характера измерения систематические погрешности подразделяют на элементарные и изменяющиеся по сложному закону.

Элементарные погрешности (рис.3) делятся на

постоянные, прогрессирующие и периодические.

Постоянные погрешности – ПИ, сохраняющие свое значение в течение времени выполнения ряда измерений.

Прогрессивные погрешности – ПИ, непрерывно возрастающие или убывающие в течение времени выполнения ряда измерений.

Например, ПИ вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.

Периодические погрешности - ПИ, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.

Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.

Всем известны "спешащие" и "отстающие" часы, погрешности которых прогрессируют во времени, но мало кто анализирует показания часов за один оборот стрелки. В результате многократного повторения вращения стрелки часов должны проявляться периодические погрешности, обусловленные эксцентриситетом и превращающиеся в нуль при завершении каждого полного оборота.

Для описания и аппроксимации систематической погрешности подбирают наиболее простую функцию, например линейную для прогрессирующей погрешности. Такой же подход применяют и для аппроксимации гармонической систематической погрешности, которая может быть описана как синусоида, косинусоида, пилообразная либо другая периодическая функция.

Систематическая погрешность может иметь не только элементарный, но и более сложный характер, который можно аппроксимировать функцией, включающей приведенные простые составляющие.

			y
		Рис. 3. Виды простейших систематических погрешностей: а – постоянные, б, в – прогрессирующие (линейная и нелинейная), г, д – прогрессирующие нелинейные (предложены варианты аппроксимации прямыми линиями), е – периодические (гармонические).

3.1.2. Сложная систематическая погрешность, включающая постоянную, прогрессирующую и периодическую составляющую, в общем виде может быть описана выражением

D_s = a + by + dsinj,

где a – постоянная составляющая сложной систематической погрешности;

y, j – соответственно аргументы прогрессирующей и периодической составляющих сложной систематической погрешности.

3.2. Случайная погрешность измерения - с оставляющая ПИ, изменяющаяся случайным образом при повторных измерениях физической величины, проведенных в одних условиях.

Случайными являются погрешности, которые обладают статистической устойчивостью (ведут себя как центрированная случайная величина).

Причиной появления таких погрешностей является совокупное действие ряда влияющих дестабилизирующих факторов, связанных с любыми источниками погрешностей, причем функциональные связи этих факторов с погрешностями определяются только стохастические зависимости, либо не могут быть выявлены из-за неопределенности действующих факторов и большого их числа.

Рассеяние результатов в ряду измерений – несовпадение результа-тов измерений одной и той же величины в ряду равноточных измерений, обусловленное действием случайных погрешностей.

Количественными оценками рассеяния результатов в ряду измере-ний являются:

- размах результатов измерений,

- средняя арифметическая погрешность,

- средняя квадратическая погрешность,

- доверительные границы погрешности.

Размах результатов измерений - о ценка R_n рассеяния результатов единичных измерений физической величины, образующих ряд (выборку) из n измерений, вычисляемая по формуле:

R_n = x_max - x_min, (1)

где x_max и x_min - наибольшее и наименьшее значения физической величины в данном ряду измерений.

Средняя квадратическая погрешность результатов единичных измерений в ряду измерений - о ценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемая по формуле

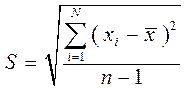, (2)

где x_i - результат i -го единичного измерения;

- среднее арифметическое значение измеряемой величины из n единичных результатов.

На практике широко распространен термин среднее квадратическое отклонение (СКО). Под отклонением в соответствии с формулой (2) понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В метрологии, это отклонение называется погрешностью измерений. Если в результаты измерений введены поправки на действие систематических погрешностей, то отклонения представляют собой случайные погрешности. Поэтому с точки зрения упорядочения совокупности терминов, родовым среди которых является термин "погрешность измерения", целесообразно применять термин " средняя квадратическая погрешность ". При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений.

СКО результата измерений среднего арифметического - о ценка случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле:

, (3)

где S - средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений; n - число единичных измерений в ряду.

Доверительные границы погрешности результата измерений – наибольшее и наименьшее значения ПИ, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое значение погрешности результата измерений.

Доверительные границы в случае нормального закона распределения вычисляются как

(4)

где - СКО, соответственно среднего арифметического результатов измерений; t - коэффициент, зависящий от доверительной вероятности P и числа измерений n.

Иногда вместо термина доверительная граница применяют термин доверительная погрешность или погрешность при данной доверительной вероятности.

Предельная погрешность измерения - м аксимальная погрешность измерения, допускаемая для данной измерительной задачи.

Суммарное СКО результата измерений -погрешность результата измерений, состоящая из суммы случайных и неисключенных систематических погрешностей, принимаемых за случайные, вычисляемая по формуле

(5)

где 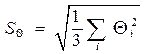- СКО суммы неисключенных систематических погрешностей при равномерном распределении.

Доверительные границы суммарной погрешности (Dx)_S могут быть вычислены по формуле

, (6)

где ;

Q - граница суммы неисключенных систематических погрешностей результата измерений, вычисляемая по формулам (7) или (8).

3.3. Погрешности, которые нельзя отнести ни к случайным, ни к систематическим из-за совершенно иного механизма образования и принципиально отличного значения, называются грубыми ПИ или промахами.

Промах -погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

Причинами возникновения грубой погрешности могут быть промах оператора при снятии отсчета или его записи, ошибка в реализации методики измерений, сбой в измерительной цепи прибора или незамеченное импульсное изменение влияющей физической величины.

Такие погрешности в принципе непредсказуемы, а их значения невозможно прогнозировать с учетом вероятности как это делают для случайных погрешностей. К ним относят:

- результаты явно не соответствующие ожидаемому результату измерений;

- экстремальные значения, принадлежность которых к массиву результатов имеет малую вероятность.

Отбрасывание (элиминация) результатов с грубыми погрешностями предупреждает возможность значительного искажения оценки результатов измерений. Исключение результатов может осуществляться либо цензурированием явно нелепых значений, либо статистическим отбраковыванием отдельных экстремальных результатов (подозрительных на наличие грубых погрешностей), которое основано на принципе практической уверенности. Применение этого принципа позволяет отбрасывать те значения, вероятность появления которых в исследуемом массиве данных меньше некоторого заранее выбранного значения.

4. Классификация ПИ по формам их математического выражения Абсолютные - ПИ выражающиеся в единицах измеряемой величины.

DХ = X_изм – Х_д

Относительные ПИ представляют собой отношение абсолютной погрешности D к значению измеряемой величины.

δХ = DХ/Х_изм

Относительные ПИ определяются в неименованных или в именованных относительных единицах. При использовании именованной относительной погрешности, выраженной в процентах

δХ = (DХ/Х_изм) ´ 100 %

Для характеристики средств измерений используют такой специфический класс относительных погрешностей, как приведенные погрешности (γХ), то есть отношение абсолютной погрешности к некоторой нормирующей величине (Х _норм)

γХ = (D /Х_норм) ´ 100 %

5. Классификация ПИ в зависимости от режима измерения Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения.

Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения.

Под статическим понимают измерение не изменяющейся по размеру, а под динамическим – изменяющейся по размеру физической величины.

Динамический режим измерений встречается не только при измерении изменяющейся величины, но и при измерении величины постоянной. И в том и в другом случаях скорость изменения сигнала измерительной информации на входе средства измерений может быть соизмерима со скоростью преобразования измерительной информации.

Например, в контрольно-сортировочных автоматах для измерения диаметров тел качения подшипников измеряется постоянная физическая величина – длина. Но из-за необходимости обеспечить высокую производительность автомата скорость изменения входного сигнала измерительной информации может оказаться выше скорости преобразования измерительной информации средством измерения. В таком случае из-за "запаздывания" с преобразованием сигнала возникают динамические погрешности.

Поскольку речь идет не столько о СИ, сколько об их работе в специфическим режиме, динамическую погрешность не следует считать инструментальной. Эту погрешность нужно рассматривать как составляющую итоговой (интегральной) погрешности, обусловленную динамическим режимом измерений.

6. Классификация ПИ по отношению к доминирующей составляющей

К пренебрежимо малым составляющим погрешностям относят погрешности, которые значительно меньше доминирующих составляющих. Формальное соотношение между пренебрежимо малой D_min и доминирующей D_max составляющими можно записать в виде

D_min << D_max.

Любую отдельную случайную или систематическую составляющую относят к пренебрежимо малым погрешностям, если она на порядок меньше доминирующей составляющей одной и той же интегральной погрешности. При объединении всех составляющих D_i в оценку интегральной погрешности D влиянием пренебрежимо малых погрешностей на окончательный результат пренебрегают.

Для одной и той же физической величины могут рассматриваться разные действительные значения. Близость их к истинному значению зависит от задачи, которая поставлена при измерении. Очевидно, что для установления годности объекта по заданному параметру точность измерения физической величины может быть значительно ниже, чем при исследовании точности технологического процесса обработки того же объекта или при сортировке однородных объектов на группы для последующей селективной сборки. Установление действительного значения измеряемой физической величины должно предваряться выбором допустимой погрешности измерений, которая и будет представлять собой предел пренебрежимо малого значения погрешности результата измерений.

Дата добавления: 2015-07-10