
ПРАКТИКУМ
по теме «Криволинейный интеграл»
Задача: Кусочно-гладкая кривая линия L на плоскости соединяет точки А и В и определяется уравнением y = y(x), [a,b] или x = x(t), y = y(t) (t1<t<t2). Вдоль кривой распределены массы с плотностью f(M) для каждой точки М. Вычислим общую массу всей системы метод интегральной суммы.
Опр. Криволинейным интегралом 1-ого рода от функции f(x,y) вдоль кривой L наз. предел интегральной суммы, полученной в результате разбиения этой кривой на малые участки с длиной siи постоянной плотностью f(xi, yi). Переменной интегрирования является длина кривой s.
J = lim 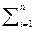 f(xi, yi)
f(xi, yi)  si
si 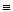
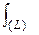 f(x,y) ds
f(x,y) ds 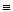
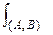 f(x,y) ds (1)
f(x,y) ds (1)
n 
Механический смысл криволинейного интеграла 1 рода: общая масса тел распределенных вдоль кривой с переменной плотностью.
Криволинейный интеграл сводится к обыкновенному определенному интегралу несколькими способами, в зависимости от способа описания кривой L.
1) Кривая L задана параметрически: x =  (t), y =
(t), y =  (t), t1
(t), t1  t
t 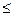 t2 .
t2 .
Тогда, длину отдельного отрезка можно представить в виде

 s =
s = 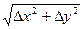 =
= 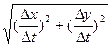
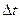 и при n
и при n 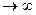
 s
s 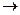 ds =
ds = 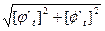 dt
dt
J = 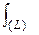 f(x,y) ds =
f(x,y) ds = 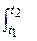 f(
f( (t),
(t), 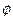 (t))
(t)) 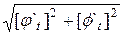 dt (2)
dt (2)
2) Кривая L задана явным уравнением: y = y(x) на [a,b].
Тогда  s =
s = 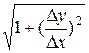
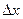 или ds =
или ds = 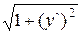 dx. В результате имеем
dx. В результате имеем
J = 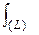 f(x,y) ds =
f(x,y) ds = 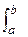 f(x,y(x))
f(x,y(x)) 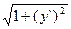 dx (3)
dx (3)
Замена в f(x,y) переменной у на y(x) означает переход к значениям функции на кривой.
При f(x,y) = 1 интеграл определяет длину дуги: S = 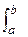
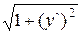 dx
dx
Пример 1. Определить длину дуги кривой y = x2/2 - 1, отсеченной осью Ох.
Решение.
Точки пересечения линий: 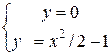
 (-
(- 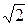 ,0), (
,0), (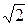 ,0)
,0)
y = x2/2 – 1, y` = x, 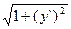 =
= 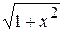 , -
, - 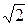
 x
x 
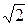
S = 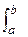
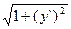 dx =
dx = 
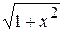 dx =
dx = 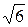 + ln (
+ ln ( )
)
Пр. 2 Найти координаты центра тяжести дуги циклоиды x = t –sin t, y = 1 –cos t, 0£ t £ p
Решение: Координаты центра тяжести однородной дуги кривой L вычисляются по формулам:  xc =
xc = 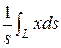 , yc =
, yc = 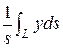 , где s – длина дуги. (4)
, где s – длина дуги. (4)
Имеем (x`t)2 + (y`t)2 = (1 – cos t)2 + (sin t)2 = 2(1 – cos t) = 4 sin2(t/2), тогда по (2)
ds = 2 sin(t/2) dt и длина дуги S = 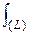 ds = 2
ds = 2 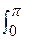 sin(t/2) dt = - 4 cos(t/2) |0p = 4
sin(t/2) dt = - 4 cos(t/2) |0p = 4
xc = 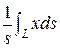 = 2/4
= 2/4 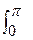 (t – sin t) sin(t/2) dt = 8/3
(t – sin t) sin(t/2) dt = 8/3
yc = 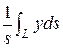 = 2/4
= 2/4 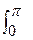 (1 – cos t) sin(t/2) dt = 4/3
(1 – cos t) sin(t/2) dt = 4/3
Задачи для самостоятельного решения
Определить длину кривой: 1) y = ln (sin x) от x = 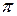 /3 до x = 2
/3 до x = 2 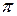 /3;
/3;
2) y = ln(1 – x2) от x = - ½ до x = ½; 3) x = t2, y = t(t2 – 3) /3 между точками пересечения с осью Ох.
Опр. Криволинейным интегралом 2-ого рода от функции f(x,y,z) вдоль пространственной кривой L наз. предел интегральной суммы, полученной в результате разбиения этой кривой на малые участки. Переменной интегрирования является не длина кривой, а её проекции на ось Оx или Оу или Oz.
J = lim 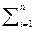 f(Mi)
f(Mi)  xi
xi 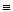
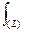 f(x,y,z) dx; J = lim
f(x,y,z) dx; J = lim 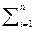 f(Mi)
f(Mi)  yi
yi 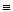
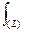 f(x,y,z) dy
f(x,y,z) dy
J = lim 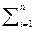 f(Mi)
f(Mi)  zi
zi 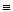
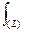 f(x,y,z) dz
f(x,y,z) dz
Объединяя эти интегралы приходим к общему виду криволинейный интеграл 2-ого рода
J = 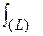 P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz
P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz 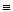
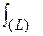 Pdx +
Pdx + 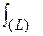 Qdy +
Qdy + 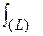 Rdz (5)
Rdz (5)
Интеграл 2-ого рода меняет знак на противоположный при изменении направления пути интегрирования.
Вычисление интегралов
1) Кривая L задана параметрически: x =  (t), y =
(t), y = 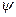 (t), z =
(t), z = 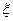 (t), t1
(t), t1 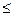 t
t 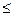 t2 .
t2 .
Тогда, dx =  `dt, dy =
`dt, dy = 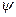 `dt, dz =
`dt, dz = 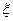 `dt и для плоской кривой имеем
`dt и для плоской кривой имеем
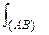 Pdx + Qdy =
Pdx + Qdy = 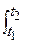 [P(
[P( (t),
(t), 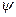 (t),
(t), 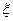 (t))
(t))  (t)` + Q(
(t)` + Q( (t),
(t), 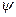 (t),
(t), 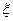 (t))
(t)) 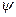 `(t)]dt (5)
`(t)]dt (5)
2) Кривая L задана явным уравнением: y = y(x) на [a,b]. Тогда dy = y`(x)dx и
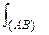 P(x,y)dx + Q(x,y)dy =
P(x,y)dx + Q(x,y)dy = 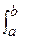 [P(x, y(x)) + Q(x,y(x)) y`(x)] dx (6)
[P(x, y(x)) + Q(x,y(x)) y`(x)] dx (6)
Замена переменной у на y(x) означает переход к значениям функции на кривой.
Пример 2. Вычислить 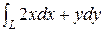 , где L: y = x2 +1 от точки А (0, 1) до точки В (1, 2)
, где L: y = x2 +1 от точки А (0, 1) до точки В (1, 2)
Решение. y = x2 + 1, dy = 2x dx, 0  x
x  1
1 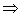
J = 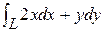 =
= 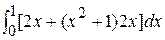 =
= 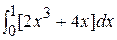 = [2x4/4 + 4x2/2]
= [2x4/4 + 4x2/2] 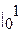 = 2,5
= 2,5
Пример 3. Вычислить J = 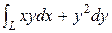 , где L: x = t2, y = t, 1 £ t £ 2.
, где L: x = t2, y = t, 1 £ t £ 2.
Решение. x = t2, dx = 2t dt, y = t, dy = 1 dt, 1 £ t £ 2 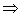
J = 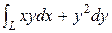 =
= 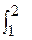 [ t2 t 2t + t2 1 ] dt = [ 2t5/5 + t3/3 ]
[ t2 t 2t + t2 1 ] dt = [ 2t5/5 + t3/3 ] 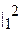 = 14
= 14 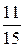
Задачи для самостоятельного решения
1) Вычислить 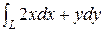 , где L: y = x2 + 1 от точки А(0, 1) до точки В(1, 2).
, где L: y = x2 + 1 от точки А(0, 1) до точки В(1, 2).
2) Вычислить 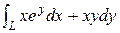 , где L: y = x2 от точки А(1, 1) до точки В(2, 4).
, где L: y = x2 от точки А(1, 1) до точки В(2, 4).
3) Вычислить  , где L: y = x от точки А(2, 2) до точки В(3, 3)
, где L: y = x от точки А(2, 2) до точки В(3, 3)
4) Вычислить 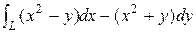 по любому пути от точки А(2, 3) до В(5, 5).
по любому пути от точки А(2, 3) до В(5, 5).
5) Вычислить 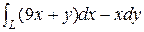 , где L: x = 2 cos t, y = 2 sin t, t Î [0, p/2].
, где L: x = 2 cos t, y = 2 sin t, t Î [0, p/2].
6) Вычислить 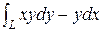 , где L: x = t2 + 1, y = t – 4, 1 £ t £ 2.
, где L: x = t2 + 1, y = t – 4, 1 £ t £ 2.
7) Вычислить 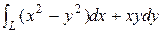 , где L: прямая от А(1,1) до В(3,4).
, где L: прямая от А(1,1) до В(3,4).
Формула Грина
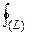 P(x,y)dx + Q(x,y)dy =
P(x,y)dx + Q(x,y)dy = 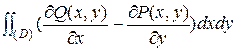 (7)
(7)
позволяет криволинейный интеграл 2 рода по контуру L свести к двойному интегралу по области D, ограниченной контуром L. Во многих случаях такая замена может существенно упростить решение задачи.
Пример 4. Вычислить J = 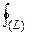 -x2y dx + xy2 dy, где L: x2 + y2 = R2 .
-x2y dx + xy2 dy, где L: x2 + y2 = R2 .
Решение. P = - x2y, 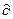 P/
P/ 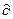 y = - x2,
y = - x2,
Q = xy2, 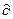 Q/
Q/ 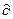 x = y2,
x = y2, 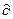 Q/
Q/ 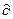 x -
x - 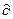 P/
P/ 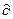 y = y2 + x2
y = y2 + x2
J = 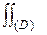 (y2 + x2) dxdy = {x = r cos
(y2 + x2) dxdy = {x = r cos  , y = r sin
, y = r sin  } =
} = 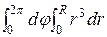 = 2
= 2 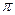 R4/4
R4/4
Пример 5. Вычислить J = 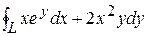 , где L: y = x2, y = 3.
, где L: y = x2, y = 3.
Решение. P = xey, 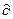 P/
P/ 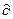 y = xey
y = xey
Q = 2x2 y, 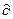 Q/
Q/ 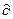 x = 4xy,
x = 4xy, 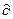 Q/
Q/ 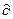 x -
x - 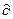 P/
P/ 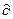 y = x(4y – ey)
y = x(4y – ey)
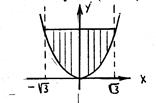
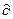 D: y = x2, y = 3;
D: y = x2, y = 3; 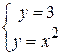
 (-
(-  ; 3), (
; 3), ( ; 3)
; 3)
Выберем коридор || Оу, его ширина - 
 x
x 
 ,
,
а движение по коридору от y = x2 до y = 3.
D:- x, x2 y 3
J = 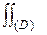 x(4y – ey) dxdy =
x(4y – ey) dxdy = 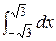
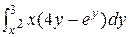 , J1 =
, J1 = 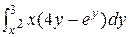 =
=
= x(2y2 – ey) 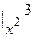 = 18x – xe3 – 2x5 + x
= 18x – xe3 – 2x5 + x 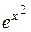 , J =
, J = 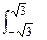 [18x – xe3 – 2x5 + x
[18x – xe3 – 2x5 + x 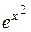 ] dx =
] dx =
= 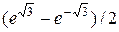
 = sh
= sh 
Задачи для самостоятельного решения
По формуле Грина вычислить следующие интегралы:
1) J = 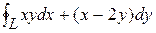 , где L: y = 6 – x2, y = 3.
, где L: y = 6 – x2, y = 3.
2) J = 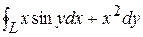 , где L: y = x2, y = 2, x = 0.
, где L: y = x2, y = 2, x = 0.
3) J = 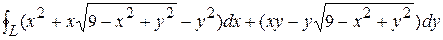 , где L: x2 + y2 = x.
, где L: x2 + y2 = x.
4) J =  , где L: xy = 1, x = 0, y = 1, y = 2.
, где L: xy = 1, x = 0, y = 1, y = 2.
5) J = 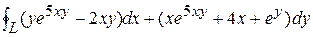 , где L: x2 + y2 = 4.
, где L: x2 + y2 = 4.
Условия независимости
от пути интегрирования криволинейных интегралов 2 рода вдоль кривой L от т.А до т.В:
1) если его значение по произвольному замкнутому контуру равно 0
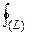 Pdx + Qdy + Rdz = 0 (8)
Pdx + Qdy + Rdz = 0 (8)
2) если его подынтегральное выражение является полным дифференциалом функции трех переменных U(x,y,z)
Pdx + Qdy + Rdz = dU (9)
3) если выполняются следующие равенства для частных производных от подынтегральных функций
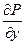 =
= 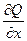 ,
, 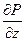 =
= 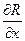 ,
,  =
= 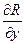 (10)
(10)
 В случае выполнения этих условий вычисляют первообразную функцию U(x,y,z) по полному дифференциалу. Для этого проводят интегрирование dU от А(x0,y0,z0) до В(x,y,z) по контуру, состоящему из прямых || координатным осям и получают сумму трех простейших определенных интегралов.
В случае выполнения этих условий вычисляют первообразную функцию U(x,y,z) по полному дифференциалу. Для этого проводят интегрирование dU от А(x0,y0,z0) до В(x,y,z) по контуру, состоящему из прямых || координатным осям и получают сумму трех простейших определенных интегралов.
Интегрирование dU(х,у) = P(x,y)dx + Q(x,y)dy
от А(x0,y0) до В(x,y) по такому контуру дает
U(x,y) = 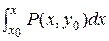 +
+ 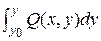 + С (11)
+ С (11)
Пример 6. Вычислить J = 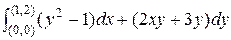
Решение. Т.к. 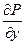 =
= 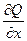 = 2у, то интеграл не зависит от пути.
= 2у, то интеграл не зависит от пути.
Вычислим интеграл вдоль ломаной ОАВ, где А(1,0), В(1,2)
ОА: y = 0, dy = 0, 0  x
x  1
1 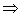 JOA =
JOA = 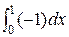 = - 1
= - 1
AB: x = 1, dx = 0, 0  y
y  2
2  JAB =
JAB =  = 10; J = JOA + JAB = 9
= 10; J = JOA + JAB = 9
Пример 7. Найти U(x,y), если dU = x sin 2y dx + x2cos 2y dy
Решение. Проверка на полный дифференциал 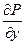 =
= 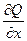 = 2x cos2y. В формуле (11) положим А(0,0). Тогда U(x,y) =
= 2x cos2y. В формуле (11) положим А(0,0). Тогда U(x,y) = 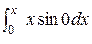 +
+ 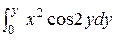 + С = ½ x2sin2y + C
+ С = ½ x2sin2y + C
Проверка: 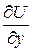 = x2cos 2y,
= x2cos 2y, 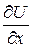 = x sin 2y.
= x sin 2y.
Дата добавления: 2015-07-10; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Значимое напоминание. | | | Управление дебиторской задолженностью |