
Читайте также:
|
1-е занятие. Вычисление двойных интегралов.
Повторить: определение, свойства, правила вычисления двойного интеграла.
1. Если область интегрирования 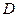 ограничена слева и справа прямыми
ограничена слева и справа прямыми 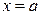 и
и 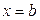
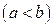 , а снизу и сверху – непрерывными кривыми
, а снизу и сверху – непрерывными кривыми 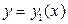 и
и 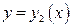 , каждая из которых пересекается вертикальной прямой только в одной точке, то
, каждая из которых пересекается вертикальной прямой только в одной точке, то
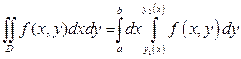 ,
,
причём сначала вычисляется внутренний интеграл 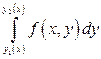 , в котором
, в котором 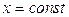 .
.
2. Если область интегрирования 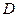 ограничена снизу и сверху прямыми
ограничена снизу и сверху прямыми 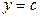 и
и 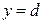
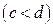 , а слева и справа – непрерывными кривыми
, а слева и справа – непрерывными кривыми 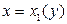 и
и 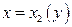 , каждая из которых пересекается вертикальной прямой только в одной точке, то
, каждая из которых пересекается вертикальной прямой только в одной точке, то
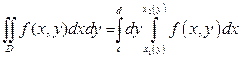 ,
,
причём сначала вычисляется внутренний интеграл 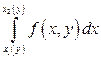 , в котором
, в котором 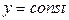 .
.
3. В общем случае, область интегрирования путём разбиения на части сводится к основным областям.
Задания для решения.
I. Вычислить двойной интеграл.
1). 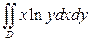 , если область
, если область 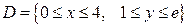 - прямоугольник.
- прямоугольник.
Решение. 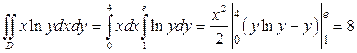 .
.
2). 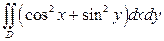 , если
, если 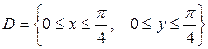 - квадрат. Ответ:
- квадрат. Ответ: 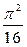 . Указание. Использовать формулы
. Указание. Использовать формулы 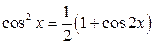 ;
; 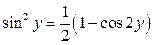 .
.
3). 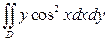 , где
, где 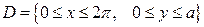 . Ответ:
. Ответ: 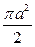 .
.
4). 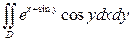 , если
, если 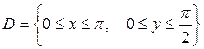 .
.
Ответ: 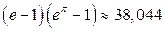 .
.
II. Вычислить повторный интеграл.
1). 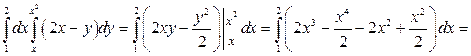
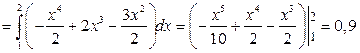 .
.
2). 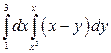 . Ответ:
. Ответ: 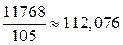 .
.
III. Вычислить двойной интеграл по заданной области.
1). 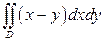 , если область
, если область 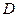 ограничена линиями
ограничена линиями 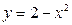 ,
, 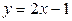 .
.
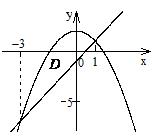 Решение. Построим линии и определим точки их пересечения:
Решение. Построим линии и определим точки их пересечения: 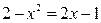 , откуда
, откуда
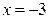 или
или 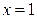 , тогда
, тогда 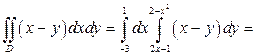
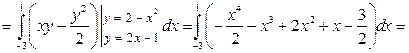
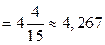 .
.
2). 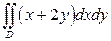 , если область
, если область 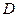 ограничена линиями
ограничена линиями 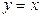 ,
, 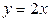 ,
, 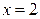 ,
, 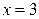 . 3).
. 3). 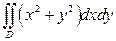 , если область
, если область 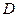 ограничена линиями
ограничена линиями 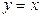 ,
, 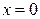 ,
, 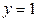 ,
, 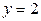 .
.
4). 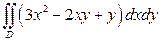 , если область
, если область 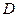 ограничена линиями
ограничена линиями 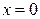 ,
, 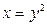 ,
, 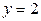 .
.
5). 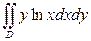 , если область
, если область 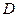 ограничена линиями
ограничена линиями 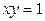 ,
, 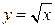 ,
, 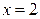 .
.
6). 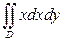 , если область
, если область 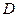 - треугольник с вершинами
- треугольник с вершинами 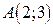 ,
, 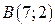 ,
, 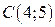 .
.
Ответы: 2). 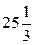 ; 3).
; 3). 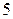 ; 4).
; 4). 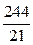 ; 5).
; 5). 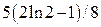 ; 6).
; 6). 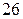 .
.
2-е занятие. Изменение порядка интегрирования и замена переменной в двойном интеграле.
Повторить: свойства иправила вычисление двойных интегралов, полярную систему координат.
I. План решения первой задачи.
1. Изобразить область, ограниченную заданными линиями.
2. Определить функции, обратные к данным линиям.
3. Меняем порядок интегрирования, для чего заданную область представим в виде одной или объединения нескольких областей другого вида.
4. Записываем двойной интеграл или сумму двойных интегралов.
Задания для решения. Изменить порядок интегрирования в интегралах.
1). 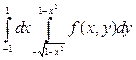 . 2).
. 2). 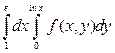 . 3).
. 3). 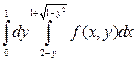 . 4).
. 4). 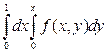 . 5).
. 5). 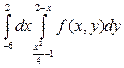 . 6).
. 6). 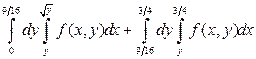 .
.
Решение. 1). Область 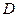 ограничена линиями
ограничена линиями 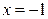 ,
, 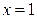 ,
, 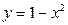 ,
, 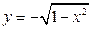 , откуда
, откуда 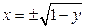 и
и 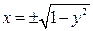 . Изменим порядок интегрирования, для
. Изменим порядок интегрирования, для 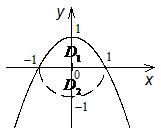 чего заданную область представим в виде двух областей
чего заданную область представим в виде двух областей 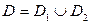 другого вида:
другого вида: 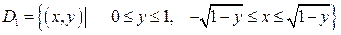 и
и 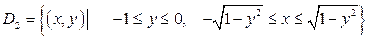 . Тогда
. Тогда 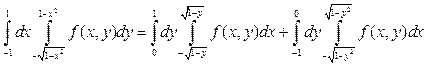 .
.
Ответы. 2). 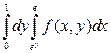 . 3).
. 3). 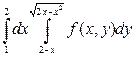 . 4).
. 4). 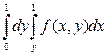 .
.
5). 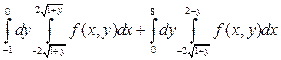 . 6).
. 6). 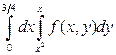 .
.
II. Рассмотрим частный случай замены переменной в двойном интеграле – переход к полярной системе координат. При этом 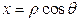 ,
, 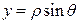 , якобиан перехода
, якобиан перехода 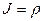 , тогда
, тогда 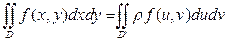 .
.
Задания для решения. Вычислить двойные интегралы, переходя к полярной системе координат.
1). 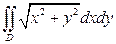 , если
, если 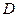 - I четверть круга
- I четверть круга 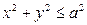 .
.
Решение. Пусть 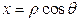 ,
, 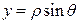 , тогда
, тогда 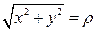 . В первой четверти
. В первой четверти 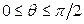 ,
, 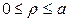 и
и 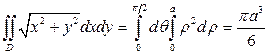 .
.
2). 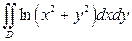 , если область
, если область 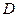 - кольцо между окружностями
- кольцо между окружностями 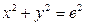 и
и 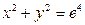 . Ответ:
. Ответ: 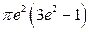 .
.
Указание. Применить формулу интегрирования по частям в определённом интеграле.
3). 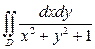 , где
, где 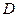 ограничена полуокружностью
ограничена полуокружностью 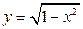 и осью
и осью 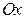 .
.
Ответ: 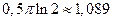 .
.
4). 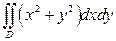 , если
, если 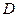 - окружность
- окружность 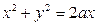 . Ответ:
. Ответ: 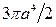 .
.
3-е занятие. Вычисление площади плоской фигуры.
Повторить: формулы для вычисления площади плоской фигуры в прямоугольных и полярных координатах.
1. Площадь плоской фигуры, ограниченной областью 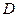 находится по формуле:
находится по формуле:
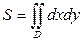 .
.
2. Если 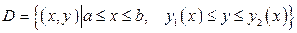 , то
, то 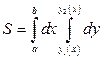 .
.
3. Если 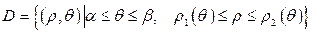 , то
, то 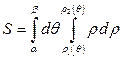 .
.
Задания для решения.
I. Найти площадь фигуры в прямоугольных координатах.
1). Вычислить площадь фигуры, ограниченной линиями 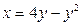 ,
, 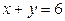 .
.
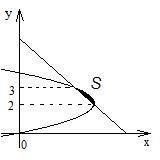 Решение. Определим точки пересечения линий из уравнения
Решение. Определим точки пересечения линий из уравнения 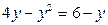 . Получим точки
. Получим точки 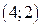 и
и 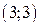 . Поэтому
. Поэтому 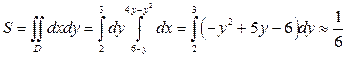 кв. ед.
кв. ед.
2). 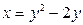 ,
, 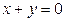 .
.
3). 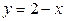 ,
, 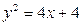 .
.
4). 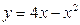 ,
, 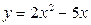 .
.
5). 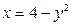 ,
, 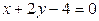 .
.
Ответы: 2). 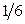 кв. ед. 3).
кв. ед. 3). 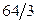 кв. ед. 4).
кв. ед. 4). 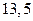 кв. ед. 5).
кв. ед. 5). 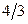 кв. ед.
кв. ед.
II. Найти площадь фигуры в полярных координатах.
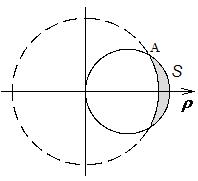 1). Вычислить площадь фигуры, ограниченной окружностями
1). Вычислить площадь фигуры, ограниченной окружностями 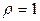 ,
, 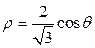 (вне окружности
(вне окружности 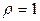 ).
).
Решение. Найдём координаты точки 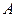 :
: 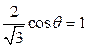 ,
, 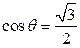 ,
, 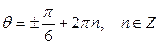 . Значит
. Значит 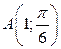 , тогда
, тогда 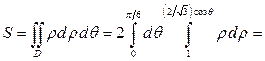
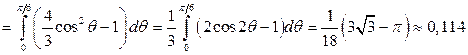 кв. ед.
кв. ед.
2). 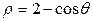 ,
, 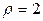 (вне кардиоиды).
(вне кардиоиды).
3). 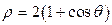 ,
, 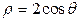 .
.
Ответы: 2). 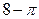 кв. ед. 3).
кв. ед. 3). 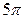 кв.ед.
кв.ед.
III. Найти площадь фигуры переходом к полярной системе координат.
1). Вычислить площадь, ограниченную лемнискатой 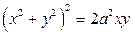 .
.
Решение. Перейдём к полярным координатам по формулам 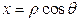 ,
, 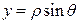 , получим
, получим 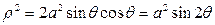 . Фигура симметрична относительно начала координат, поэтому изменение
. Фигура симметрична относительно начала координат, поэтому изменение 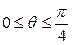 соответствует четверти искомой площади, значит
соответствует четверти искомой площади, значит 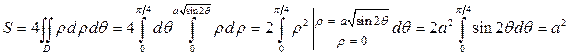 .
.

2). Найти площадь фигуры, ограниченной линией 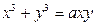 (петля).
(петля).
Указание. Осью симметрии петли является 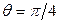 . В полученном интеграле сделать замену переменной
. В полученном интеграле сделать замену переменной 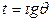 . Ответ:
. Ответ: 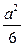 .
.
4-е занятие. Вычисление тройных интегралов.
Повторить: правило вычисления тройного интеграла, цилиндрические и сферические координаты.
1. Если 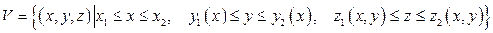 , то
, то
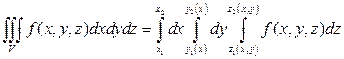 .
.
2. Цилиндрические координаты: 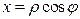 ,
, 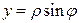 ,
, 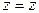 . При этом
. При этом 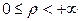 ,
, 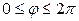 ,
, 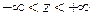 . Якобиан преобразования
. Якобиан преобразования 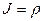 , поэтому
, поэтому
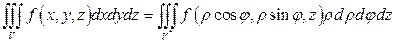 .
.
3. Сферические координаты (их называют полярными координатами в пространстве): 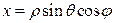 ,
, 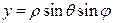 ,
, 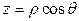 . При этом
. При этом 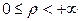 ,
, 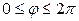 ,
, 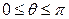 . Якобиан преобразования
. Якобиан преобразования 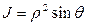 , поэтому
, поэтому
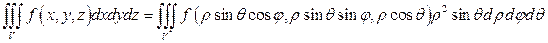 .
.
Задания для решения.
I. Вычислить тройной интеграл по заданной области.
1). 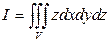 , где область
, где область 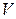 определяется неравенствами
определяется неравенствами 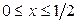 ,
, 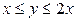 ,
, 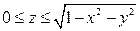 .
.
Решение. 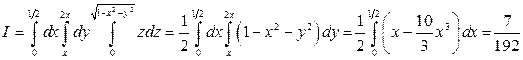 .
.
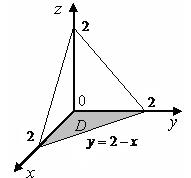 2).
2). 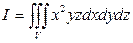 , если область
, если область 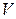 ограничена плоскостями
ограничена плоскостями 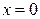 ,
, 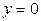 ,
, 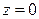 ,
, 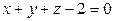 .
.
Решение. Область 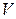 ограничена сверху плоскостью
ограничена сверху плоскостью 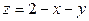 , а снизу – плоскостью
, а снизу – плоскостью 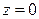 . Проекцией тела на плоскость
. Проекцией тела на плоскость 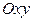 служит область
служит область 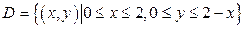 . Следовательно,
. Следовательно, 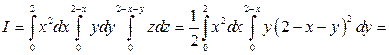
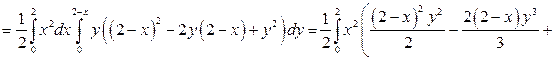
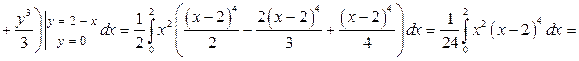
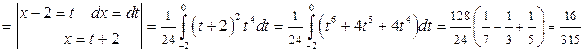 .
.
3). 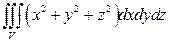 , если
, если 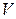 - прямоугольный параллелепипед, определяемый неравенствами
- прямоугольный параллелепипед, определяемый неравенствами 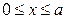 ,
, 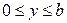 ,
, 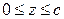 . Ответ:
. Ответ: 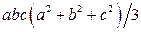 .
.
4). 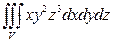 , если тело
, если тело 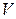 ограничено поверхностями
ограничено поверхностями 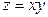 ,
, 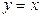 ,
, 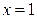 ,
, 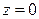 . Ответ:
. Ответ: 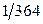 .
.
II. Вычислить тройной интеграл переходом к цилиндрической или сферической системе координат.
1). 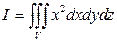 , если
, если 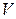 - шар
- шар 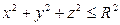 .
.
Решение. Перейдём к сферическим координатам. В области 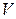 :
: 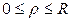 ,
, 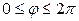 ,
, 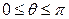 , тогда
, тогда 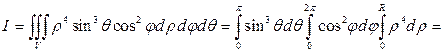
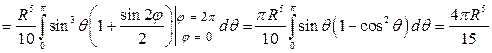 .
.
2). 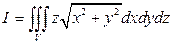 , если область
, если область 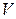 ограничена цилиндром
ограничена цилиндром 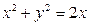 и плоскостями
и плоскостями 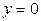 ,
, 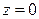 ,
, 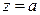 .
.
Решение. Перейдём к цилиндрическим координатам. Уравнение цилиндра в этих координатах примет вид 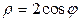 . Следовательно, в области
. Следовательно, в области 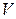 :
: 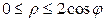 ,
, 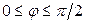 (т. к.
(т. к. 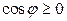 ),
), 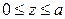 . Поэтому
. Поэтому 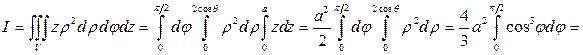
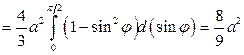 .
.
3). 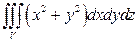 , если область
, если область 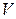 - верхняя половина шара
- верхняя половина шара 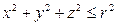 .
.
Ответ: 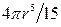 .
.
4). 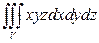 , если область
, если область 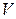 ограничена сферой
ограничена сферой 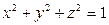 и плоскостями
и плоскостями 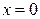 ,
, 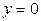 ,
, 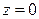 . Ответ:
. Ответ: 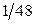 .
.
5). 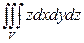 , если область
, если область 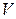 ограничена конусом
ограничена конусом 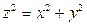 и плоскостью
и плоскостью 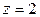 . Ответ:
. Ответ: 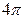 .
.
5-е занятие. Приложения тройного интеграла.
Повторить: формулы объёма и массы тела, координаты центра тяжести.
1. Объём тела вычисляется по формуле: 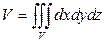 .
.
2. Если дано некоторое тело 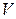 с плотностью
с плотностью 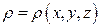 - непрерывной функцией, то масса данного тела:
- непрерывной функцией, то масса данного тела: 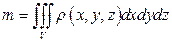 .
.
3. Координаты центра тяжести однородного тела: 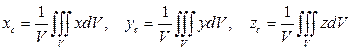 , где
, где 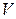 - объём данного тела.
- объём данного тела.
Задания для решения.
1). Вычислить объём тела, ограниченного поверхностями 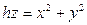 .
.
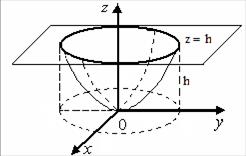 Решение. Данное тело ограничено снизу параболоидом
Решение. Данное тело ограничено снизу параболоидом 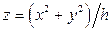 , сверху плоскостью
, сверху плоскостью 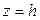 и проецируется в круг
и проецируется в круг 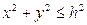 плоскости
плоскости 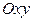 . Переходим к цилиндрическим координатам, в которых уравнение параболоида
. Переходим к цилиндрическим координатам, в которых уравнение параболоида 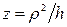 . Объём тела
. Объём тела 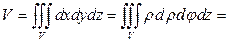
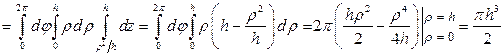 куб. ед.
куб. ед.
2). Вычислить объём тела, ограниченного поверхностями 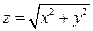 ,
, 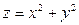 .
.
Ответ: 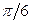 куб. ед.
куб. ед.
3). Найти массу куба 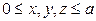 , если плотность в каждой точке
, если плотность в каждой точке 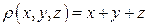 . Ответ:
. Ответ: 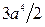 .
.
4). Найти координаты центра тяжести призмы, ограниченной плоскостями 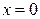 ,
, 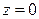 ,
, 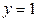 ,
, 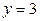 ,
, 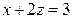 .
.
Решение. Объём тела 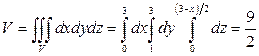 куб. ед. Тогда
куб. ед. Тогда 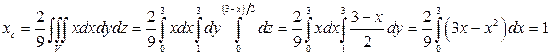 ,
,
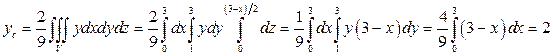 ,
,
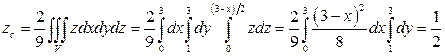 . Ответ:
. Ответ: 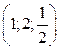 .
.
5). Найти координаты центра тяжести тела, ограниченного поверхностями 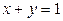 ,
, 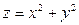 ,
, 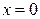 ,
, 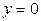 ,
, 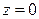 . Ответ:
. Ответ: 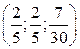 .
.
6). Найти координаты центра тяжести тела, ограниченного поверхностями 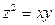 ,
, 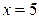 ,
, 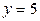 ,
, 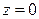 . Ответ:
. Ответ: 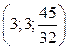 .
.
6-е занятие. Контрольная работа по теме «Кратные интегралы».
Повторить: приёмы и способы вычисления двойных и тройных интегралов.
Примерный вариант контрольной работы.
1. Вычислить интеграл 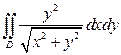 , где D ограничена окружностями
, где D ограничена окружностями 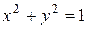 ,
, 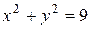 .
.
2. Вычислить интеграл 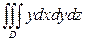 , где область D ограничена плоскостями
, где область D ограничена плоскостями 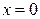 ,
, 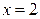 ,
, 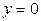 ,
, 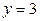 ,
, 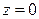 ,
, 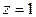 .
.
3. а). Построить на плоскости XOY область интегрирования 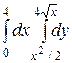 заданного интеграла;
заданного интеграла;
б). Изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования.
7-е занятие. Вычисление криволинейных интегралов.
Повторить: формулы для вычисления криволинейных интегралов I и II рода.
1. Если кривая 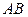 задана уравнением
задана уравнением 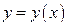 ,
, 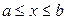 , где
, где 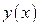 - непрерывно дифференцированная функция, то
- непрерывно дифференцированная функция, то 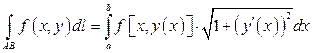 ;
;
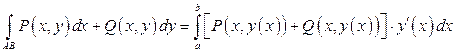 .
.
Если кривая 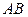 задана уравнением вида
задана уравнением вида 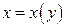 ,
, 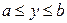 , то
, то
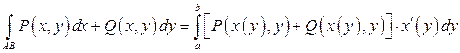 .
.
2. Если кривая задана параметрическими уравнениями 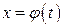 ,
, 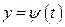 ,
, 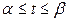 , где
, где 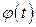 и
и 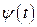 - непрерывно дифференцируемые функции, причём точке
- непрерывно дифференцируемые функции, причём точке 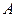 соответствует значение
соответствует значение 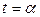 , точке
, точке 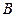 - значение
- значение 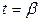 , тогда
, тогда
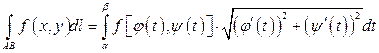 ;
;
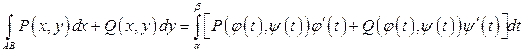 .
.
Задания для решения. Вычислить криволинейные интегралы.
1). 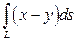 , где
, где 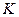 - отрезок прямой от
- отрезок прямой от 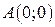 до
до 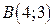 .
.
Решение. Уравнение прямой 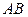
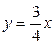 , отсюда
, отсюда 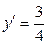 , значит
, значит 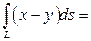
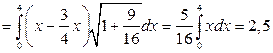 .
.
2). 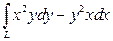 , если
, если 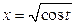 ,
, 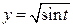 ,
, 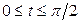 .
.
Решение. 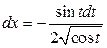 ,
, 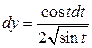 , тогда
, тогда
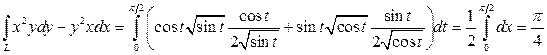 .
.
3). 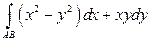 , если путь от
, если путь от 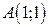 до
до 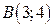 - отрезок прямой.
- отрезок прямой.
4). 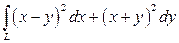 , если
, если 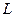 - ломаная
- ломаная 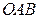 где
где 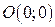 ,
, 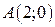 ,
, 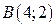 .
.
5). 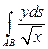 , если
, если 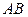 - дуга кривой
- дуга кривой 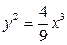 от
от 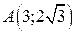 до
до 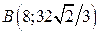 .
.
6). Найти координаты центра тяжести дуги циклоиды 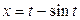 ,
, 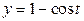 ,
, 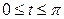 .
.
7). Найти координаты центра тяжести дуги окружности 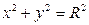 в I четверти.
в I четверти.
8). Найти массу дуги окружности 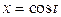 ,
, 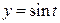 , если её плотность
, если её плотность 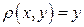 .
.
Ответы: 3). 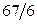 . 4).
. 4). 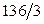 . 5).
. 5). 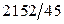 . 6).
. 6). 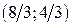 . 7).
. 7). 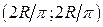 . 8). 2.
. 8). 2.
Приложение. Табличные интегралы.
1. 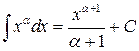 ,
, 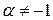 ;
; 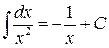 ;
; 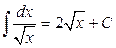 .
.
2. 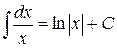 .
.
3. 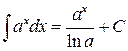 .
.
4. 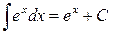 .
.
5. 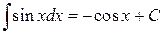 ;
; 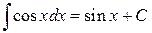 .
.
6. 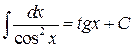 ;
; 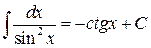 .
.
7. 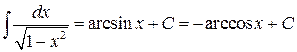 .
.
8. 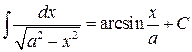 .
.
9. 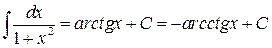 .
.
10. 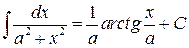 .
.
11. 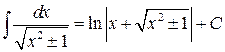 .
.
12. 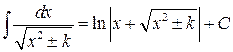 .
.
13. 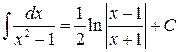 .
.
14. 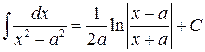 .
.
15. 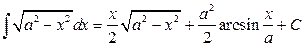 .
.
16. 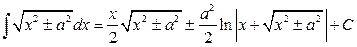 .
.
Библиография
1. П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. Высшая математика в упражнениях и задачах. 2 том.
2. Н. С. Пискунов. Дифференциальное и интегральное исчисления. 2 том.
3. Д. Письменный. Конспект лекций по высшей математике.
4. В. С. Шипачёв. Высшая математика.
5. В.П. Минорский Сборник задач по высшей математике.
В авторской редакции.
Компьютерная вёрстка Шубовича А.А.
Подписано в печать Формат 
Усл. печ. л. 0,7. Тираж 100. Заказ
Издательско-полиграфический комплекс ВГСХА «Нива»
400002, Волгоград, Университетский пр-т, 26
Дата добавления: 2015-07-10; просмотров: 54 | Нарушение авторских прав