Лемниската Бернулли

Лемниската Бернулли - геометрическое место точек, расстояние которых от двух данных точек (фокусов) является постоянной величиной, равной квадрату половины межфокусного расстояния.

,

Вершины кривой находятся в точках

Площадь каждой петли S=a ².

ПП 7.4. КРивые на плоскости

ПП 7.4. №1.

Найдите полярный угол отрезка, направленного из точки (5, ) в точку (6, ). Решение:

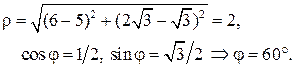
ПП 7.4. №2.

Составьте уравнение прямой в полярных координатах, считая известными расстояние р от полюса до прямой и угол a от полярной оси до луча, направленного из полюса перпендикулярно к прямой. Решение: 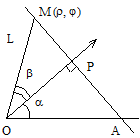Известны ОР = р, Ð РОА = a, произвольная точка М прямой L имеет координаты (r, j). Точка М лежит на прямой L в том и только в том случае, когда проекция точки М на луч ОР совпадает с точкой Р, т.е. когда р = r ×cos b, где Ð РОМ = b. Угол j = a + b и уравнение прямой L принимает вид r ×cos(j - a) = p.

r cos(j - a)= p

ПП 7.4. №3.

Найдите полярное уравнение кривой x = a, a > 0 и изобразите ее. Решение:     r×cosj = a ® r = a/cosj.    

r = a /cos j

ПП 7.4. №4.

Найдите полярное уравнение кривой y = b, b > 0 и изобразите ее. Решение: r×sinj = b ® r = b/sinj.

r = b/sinj

ПП 7.4. №5.

Найдите полярное уравнение кривой (х ² + у ²)² = а ² ху и изобразите ее. Решение: xy ³ 0, 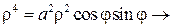. Уравнение кривой в полярных координатах имеет вид и задает двухлепестковую розу:

ПП 7.4. №6.

Постройте в полярной системе координат линию r = 2 a ×sinj, a > 0. Решение: Линия представляет собой окружность со смещенным центром: , x ² + y ² – 2 ay = 0, x ² + (y – a)² = a ^2.

Окружность

ПП 7.4. №7.

Постройте в полярной системе координат линию r = 2 + cosj. Решение: Линия представляет собой улитку Паскаля и получается, если каждый радиус-вектор окружности r = cosj увеличить на два. Найдем координаты контрольных точек: j = 0, r = 3; j = p/2, r = 2; j = p, r = 1.

Улитка Паскаля

ПП 7.4. №8.

Постройте в полярной системе координат линию . Решение:

j^(0)
(а)		0,3	0,6	0,86	0,99
j^(0)
(а)	0,99	0,86	0,6	0,3

Для нахождения вида кривой обратимся к графику функции для :

Функция при а >0 принимает допустимые, неотрицательные значения при принимает максимальные, равные а, значения при , интервалами возрастания функции являются значения , убывания – . В результате график функции принимает вид двухлепестковой розы:

Двух-лепестковая роза

ПП 7.4. №9.

Постройте в полярной системе координат линию Решение: 4 – 5×cosj > 0, cosj < 4/5, j Î (arccos(4/5), 2p – arccos(4/5)). При этом r×(4 - 5×cosj) = 9. Переходя к декартовым координатам, получаем 16 x ² + 16 y ² = 25 x ² + 90 x + 81, 9 x ² + 90 x – 16 y ² +81 = 0, 9(x + 5)² – 16 y ² = 144 ® – правая ветвь гиперболы при указанных j. Кривую можно было построить по точкам, например, при j = p r = 9/10.

Правая ветвь гиперболы

ПП 7.4. №10.

Постройте в полярной системе координат линию r²×sin2j = а ². Решение: Перейдем к декартовым координатам, учтем, что тогда кривая принимает вид гиперболы:  

Гипербола

ПП 7.4. №11.

Какая линия задается параметрическими уравнениями: 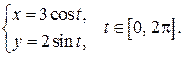Решение: - эллипс.

Эллипс

ПП 7.4. №12.

Какая линия задается параметрическими уравнениями: 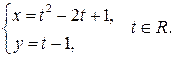Решение: у ² = x – парабола.

Парабола

ПП 7.4. №13.

Какая линия задается параметрическими уравнениями: Решение: (x + 1)² + (y – 3)² = 4 –окружность.

Окружность

ПП 7.4. №14.

Какая линия задается параметрическими уравнениями: Решение: y = -x ² – 2 x, y – 1 = -(x + 1)²– парабола с вершиной в точке (-1, 1).

Парабола

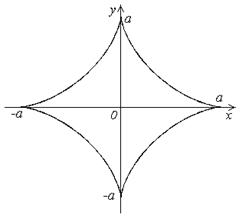
ПП 7.4. №15.

Выведите уравнение астроиды в полярной системе координат. Решение: , ; – уравнение астроиды в декартовых координа­тах. Для перехода к полярным координатам учтем, что , , , , .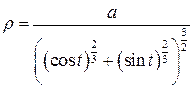

Дата добавления: 2015-07-10