
Читайте также:
|
Лабораторная работа № 7
ИЗУЧЕНИЕ ПРОЗРАЧНОЙ ДИФРАКЦИОННОЙ РЕШЕТКИ
Цель работы: определение длин волн границ видимой части спектра лампы накаливания.
Оборудование: источник света (лампа накаливания), экран со щелью и шкалой, прозрачная дифракционная решетка.
Краткие теоретические сведения
В простейшем случае дифракционная решетка представляет собой стеклянную прозрачную пластинку, на которую нанесены на одинаковом расстоянии друг от друга штрихи одинаковой ширины. В общем случае дифракционной решеткой называют любую периодическую структуру, способную повлиять на амплитуду или фазу падающей на нее электромагнитной волны. Если периодически меняющимся параметром является, например прозрачность пластинки, то решетка называется амплитудной. Если периодически изменяются коэффициент преломления или геометрическая толщина, решетка называется фазовой.
Если прозрачную дифракционную решетку расположить перпендикулярно лучам белого света, а за ней поместить собирающую линзу, то на экране в фокальной плоскости линзы появится дифракционная картина. В направлении, совпадающим с нормалью к поверхности решетки, будет видна белая полоса (дифракционный максимум нулевого порядка для всех длин волн). В направлениях, составляющих определенные углы с нормалью к поверхности решетки, наблюдаются главные дифракционные максимумы первого, второго и т.д. порядков, имеющие радужную окраску. Фиолетовый конец спектра обращен к центру дифракционной картины, красный - наружу. Дифракционные спектры расположены симметрично относительно центрального максимума и могут накладываться друг на друга.
Рассмотрим механизм возникновения описанной дифракционной картины, используя явление дифракции Фраунгофера на одной, затем на двух и, наконец, на N щелях.
Если на щель, ширина которой b, падает нормально к ее плоскости параллельный пучок света, то в фокальной плоскости объектива (на экране) наблюдается распределение интенсивности света (дифракционная картина), описываемое выражением:
Ij = I0( )2, (1)
)2, (1)
где u=  ; I0 -интенсивность падающего света; j - угол дифракции.
; I0 -интенсивность падающего света; j - угол дифракции.
Исследование Ij на экстремум позволяет определить максимумы и минимумы дифракционной картины: если в разнице между крайними лучами, падающими на щель, а затем испытывающими отклонение на угол j от первоначального направления, укладывается нечетное число длин полуволн, т. е. при
b×sin = ±(2k+1) 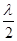 , (2)
, (2)
где k=0,1,2,3,..., то в направлении j будет наблюдаться максимум дифракционной картины. Соответственно для минимумов дифракционной картины должно выполнятся условие
b×sinj = ±2k 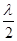 , k=1,2,3,... (3)
, k=1,2,3,... (3)
(в разности хода укладывается четное число длин полуволн).
Условия (2) и (3) легко получить, если воспользоваться методом зон Френеля.
Рассмотрение дифракции света на двух щелях, разделенных непрозрачным промежутком a, если их рассматривать как отдельные когерентные источники колебаний (аналог опыта Юнга), позволяет получить распределение интенсивности на экране в виде
I¢j = I0( )2(
)2(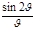 )2, (4)
)2, (4)
где
 =
=  , (5)
, (5)
(a+b)×sinj - разность хода между сходными лучами от двух щелей.
Из (4) следует, что в случае N щелей (дифракционная решетка) распределение интенсивности падающего света, формируемое дифракционной решеткой, будет иметь вид
Ij =I0( )2(
)2( )2. (6)
)2. (6)
Последний множитель выражения (6) учитывает интерференцию сходных (подобных) лучей от N щелей. Исследование (6) на экстремум дает условие для наблюдения главных максимумов
d×sinj = ±kl, (7)
в котором d = a + b - период дифракционной решетки; k=0,1,2,3,...
Для главных минимумов имеем:
b×sinj = ±k l, (8)
где k=1,2,3,....
Кроме главных максимумов и минимумов, наблюдаются дополнительные минимумы и максимумы соответственно при условиях:
d×sinj = ±( )l, (9)
)l, (9)
где k  0,N,2N,....., k=1,2...,N-1....;
0,N,2N,....., k=1,2...,N-1....;
d×sinj = ±(k+  )l, (10)
)l, (10)
где m=1,2,3,...,N-2.
Таким образом, число главных максимумов в N раз меньше общего числа минимумов. Между двумя главными максимумами находятся N-1 минимумов и N-2 дополнительных максимумов. Интенсивность последних мала.
Для данного угла дифракции j при совпадении максимумов (7) и минимумов (8) часть главных максимумов исчезает. Условие исчезновения максимумов имеет вид
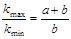 . (11)
. (11)
Интенсивность линий k-го порядка растет квадратично с увеличением числа щелей и обратно пропорционально квадрату порядка спектра:
Ik=  , (12)
, (12)
В центре дифракционной картины от решетки, где j=0, лежит не разложенный по длинам волн белый свет - спектр нулевого порядка, интенсивность которого
I=I0 N2. (13)
На рис.1 приведена дифракционная картина, получающаяся от решетки с четырьмя щелями (N=4).
Дата добавления: 2015-07-10; просмотров: 61 | Нарушение авторских прав