Проверка гипотезы о сравнении выборочной средней с генеральной средней

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ.

Гипотезы о средних (о математических ожиданиях).

Сравнение выборочной средней с математическим ожиданием.

Методические указания к практическим занятиям

по дисциплине «Математическая статистика»

Составители: Егорова Ю.Б.

Мамонов И.М.

МОСКВА 2009

Проверка статистических гипотез. Гипотезы о средних (о математических ожиданиях). Сравнение выборочной средней с математическим ожиданием: Методические указания к практическим занятиям по дисциплине «Математическая статистика»/ Ю.Б. Егорова, И.М. Мамонов. М.: МАТИ, 2009. – 16 с.

ÓЕгорова Ю.Б.,

Мамонов И.М.,

составление, 2009

Ó МАТИ, 2009

ВВЕДЕНИЕ

Методические указания предназначены для студентов дневного отделения факультета №14 специальностей 230102, 220231 и являются учебным руководством при выполнении индивидуального задания. В настоящее время существует достаточно большое количество статистических программ, предназначенных для работы на персональном компьютере. Однако для лучшего понимания изучаемого материала индивидуальное задание рекомендуется выполнить «вручную» (с помощью калькулятора).

ПРОВЕРКА ГИПОТЕЗЫ О СРАВНЕНИИ ВЫБОРОЧНОЙ СРЕДНЕЙ С ГЕНЕРАЛЬНОЙ СРЕДНЕЙ

(С МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ)

1.1. Генеральная дисперсия известна (большая выборка n ≥30)

Пусть генеральная совокупность исследуемой случайной величины Х распределена нормально: Х~N(m,σ). Предположим, что генеральная дисперсия D(X)=σ² известна, например, по многолетним наблюдениям, или задана по проекту, или найдена теоретически, или вычислена по выборке большого объема (n ≥30).

Из генеральной совокупности Х сделаем выборку объемом n. Найдем выборочное среднее .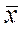

При заданном уровне значимости α необходимо проверить нулевую гипотезу, состоящую в том, что выборочное среднее и математическое ожидание различаются незначимо, т.е. математическое ожидание (генеральное среднее) равно значению m₀:

Н_о: М(Х)= m₀.

Сравнение производится с помощью специально подобранной случайной величины – статистического критерия U, имеющего нормированный нормальный закон распределения с параметрами М(U) = m_u= 0, σ(U)= 1:

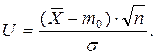
Критическая область строится в зависимости от вида альтернативной (конкурирующей) гипотезы.

Первый случай.

Выдвигаем нулевую гипотезу Н_о: М(Х)= m₀.

Выдвигаем альтернативную гипотезу Н₁: М(Х)≠ m₀.

В этом случае строят двустороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия .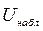

2) по таблице функции Лапласа (см. Приложение 1) определяем критическое значение критерия 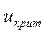из равенства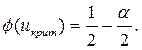

3) Если 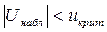, то нулевая гипотеза принимается.

Если 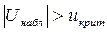, то нулевая гипотеза отвергается и принимается альтернативная.

Второй случай.

Выдвигаем нулевую гипотезу Н_о: М(Х)= m₀.

Выдвигаем альтернативную гипотезу Н₁: М(Х)> m₀.

В этом случае строят правостороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия .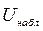

2) по таблице функции Лапласа (см. Приложение 1) определяем критическое значение критерия 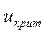из равенства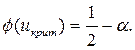

1) Если 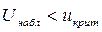, то нулевая гипотеза принимается.

Если 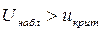, то нулевая гипотеза отвергается и принимается альтернативная.

Третий случай.

Выдвигаем нулевую гипотезу Н_о: М(Х)= m₀.

Выдвигаем альтернативную гипотезу Н₁: М(Х)< m₀.

В этом случае строят левостороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия .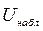

2) по таблице функции Лапласа (см. Приложение 1) определяем критическое значение критерия 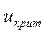из равенства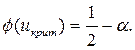

3) Если 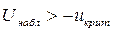, то нулевая гипотеза принимается.

Если 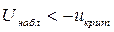, то нулевая гипотеза отвергается и принимается альтернативная.

ПРИМЕР 1. Техническая норма предусматривает в среднем 21 сек. на выполнение определенной технологической операции на конвейере по сборке часов. От работающих на этой операции поступили жалобы, что в действительности они затрачивают на нее больше времени. Для проверки были проведены измерения времени выполнения этой операции у 36 работниц. Получено среднее время выполнения операции 21,6 сек, выборочное среднее квадратическое отклонение 0,36 сек. Можно ли по данным выборки считать, что среднее время выполнения операции соответствует норме?

РЕШЕНИЕ. По условию n =36; 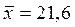сек; σ ≈ σ*(X)= 100 сек, m₀ =21 сек. Выберем уровень значимости α =0,05.

Выдвигаем нулевую гипотезу Н_о: М(Х)= m₀. Относительно альтернативной гипотезы возможны два случая: а) М(Х)≠m₀; б) Н₁: М(Х)> m₀ (так как 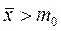). Рассмотрим эти случаи.

а) Н_о: М(Х)= 21 сек.

Н₁: М(Х)≠ 21 сек.

В этом случае строят двустороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия:

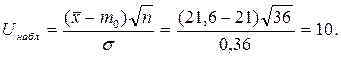
2) по таблице функции Лапласа (см. Приложение 1) определяем критическое значение критерия 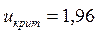из равенства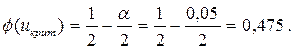

3) Так как 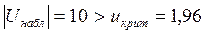, то нулевая гипотеза отвергается и принимается альтернативная.

б) Н_о: М(Х)= 21 сек.

Н₁: М(Х)> 21 сек.

В этом случае строят правостороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия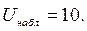

2) по таблице функции Лапласа (см. Приложение 1) определяем критическое значение критерия 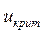=1,645 из равенства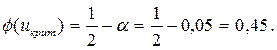

3) Так как 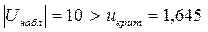, то нулевая гипотеза отвергается и принимается альтернативная.

Таким образом, с вероятностью 0,95 можно утверждать, что выборочное среднее и математическое ожидание (генеральное среднее) различаются значимо и, следовательно, жалобы работниц обоснованы.

1.2. Генеральная дисперсия неизвестна (малые выборки n <30)

Пусть генеральная совокупность исследуемой случайной величины Х распределена нормально: Х~N(m,σ). Пусть генеральная дисперсия D(X) неизвестна. Из генеральной совокупности Х сделаем выборку объемом n. Найдем выборочную среднюю 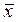и «исправленную» дисперсию .

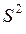При заданном уровне значимости α необходимо проверить нулевую гипотезу, состоящую в том, что выборочная средняя и математическое ожидание различаются незначимо, т.е. математическое ожидание (генеральное среднее) равно значению m₀:

Н_о: М(Х)= m₀.

Сравнение производится с помощью специально подобранной случайной величины – статистического критерия Т, имеющего закон распределения Стьюдента с k=n-1 степенями свободы:

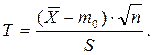
Критическая область строится в зависимости от вида альтернативной (конкурирующей) гипотезы.

Первый случай.

Выдвигаем нулевую гипотезу Н_о: М(Х)= m₀.

Выдвигаем альтернативную гипотезу Н₁: М(Х)≠ m₀.

В этом случае строят двустороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия .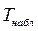

2) по таблице критических точек распределения Стьюдента (см. Приложение 2) определяем критическое значение критерия 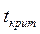для двусторонней критической области в зависимости от уровня значимости α и числа степеней свободы k=n- 1.

3) Если 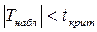, то нулевая гипотеза принимается.

Если 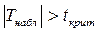, то нулевая гипотеза отвергается и принимается альтернативная.

Второй случай.

Выдвигаем нулевую гипотезу Н_о: М(Х)= m₀.

Выдвигаем альтернативную гипотезу Н₁: М(Х)> m₀.

В этом случае строят правостороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия .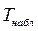

2) по таблице критических точек распределения Стьюдента (см. Приложение 2) определяем критическое значение критерия 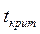для односторонней критической области в зависимости от уровня значимости α и числа степеней свободы k=n- 1.

3) Если 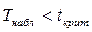, то нулевая гипотеза принимается.

Если 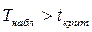, то нулевая гипотеза отвергается и принимается альтернативная.

Третий случай.

Выдвигаем нулевую гипотезу Н_о: М(Х)= m₀.

Выдвигаем альтернативную гипотезу Н₁: М(Х)< m₀.

В этом случае строят левостороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия .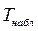

2) по таблице критических точек распределения Стьюдента (см. Приложение 2) определяем критическое значение критерия 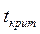для односторонней критической области в зависимости от уровня значимости α и числа степеней свободы k=n- 1.

3) Если 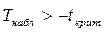, то нулевая гипотеза принимается.

Если 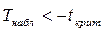, то нулевая гипотеза отвергается и принимается альтернативная.

ПРИМЕР 2. Производители нового типа аспирина утверждают,

что он снимает головную боль за 30 мин. Случайная выборка 25 человек, страдающих головными болями, показала, что новый тип аспирина снимает головную боль за 28,6 мин при среднем квадратическом отклонении 4,2 мин. Проверьте при уровне значимости 0,05 справедливость утверждения производителей аспирина о том, что это лекарство излечивает головную боль за 30 мин.

РЕШЕНИЕ. По условию n =25; 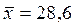мин; S= 4,2 мин; m₀ =30 мин; α =0,05.

Выдвигаем нулевую гипотезу Н_о: М(Х)= m₀. Относительно альтернативной гипотезы возможны два случая: а) М(Х)≠m₀; б) Н₁: М(Х)< m₀ (так как 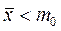). Рассмотрим эти случаи.

а) Н_о: М(Х)= 30 мин.

Н₁: М(Х)≠ 30 мин.

В этом случае строят двустороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) по выборке определяем наблюдаемое значение критерия :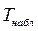

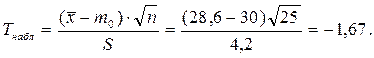
2) по таблице критических точек распределения Стьюдента (см. Приложение 2) определяем критическое значение критерия 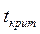=2,06 для двусторонней критической области в зависимости от уровня значимости α =0,05 и числа степеней свободы k=n- 1=25-1=24.

3) Так как 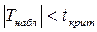, то нулевая гипотеза принимается.

б) Н_о: М(Х)= 30 мин.

Н₁: М(Х)< 30 мин.

В этом случае строят левостороннюю критическую область.

Порядок проверки нулевой гипотезы:

1) определяем наблюдаемое значение критерия 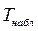=-1,67.

2) по таблице критических точек распределения Стьюдента (см. Приложение 2) определяем критическое значение критерия 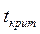=1,71 для односторонней критической области в зависимости от уровня значимости α =0,05 и числа степеней свободы k=n- 1=25-1=24.

3) Так как 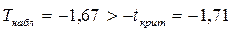, то Н_о принимается.

Таким образом, с вероятностью 0,95 можно утверждать, что выборочное среднее и математическое ожидание (генеральное среднее) различаются незначимо и, следовательно, утверждение производителей аспирина о том, что это лекарство излечивает головную боль за 30 мин, справедливо.

Дата добавления: 2015-07-12