Вихідні дані

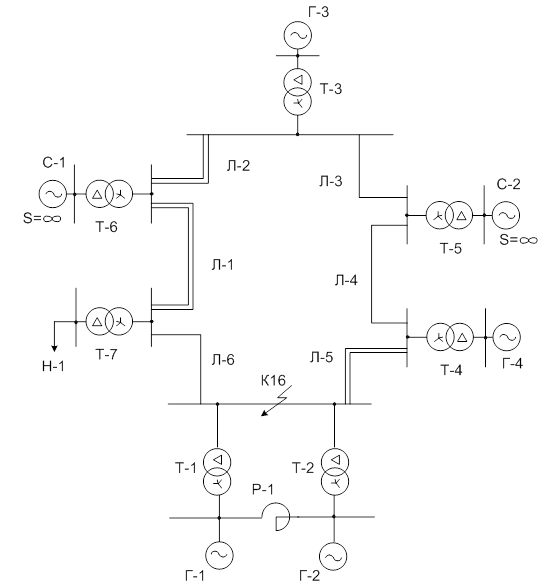
Рис. 1 — Розрахункова схема електричної системи

Характеристика генераторів

Генератори	Параметри генераторів
SН, МВA	UН, кВ	x”d
Г-1; Г-2;		10,5	0,132
Г-3; Г-4.		10,5	0,19

Характеристика трансформаторів

Трансформатори	Параметри трансформаторів
SН, МВА	UН, кВ	UК, %
ВН	СН	НН	В–Н	С–Н	В–С
Т-1; Т-2			–	10,5	10,5	–	–
Т-3; Т-4			–	10,5	10,5	–	–
Т-5; Т-7			–	10,5	6,5	–	–
Т-6			–	10,5		–	–

Характеристика навантаження

Навантаження	Параметри навантаження
SН, МВА	UН, кВ
Н-1		10,5

Характеристика реакторів

Реактор	Параметри реакторів
UН, кВ	UК, %	IН, кА
Р-1			2,5

Характеристика ліній електропередачі

ЛЕП	Параметри ЛЕП
Тип	L, км	х1 УД, Ом/км	х0/ х1
Л-1	ВЛ		0,41
Л-2	ВЛ		0,40	3,5
Л-3	ВЛ		0,42
Л-4	ВЛ		0,43
Л-5	ВЛ		0,41	2,5
Л-6	ВЛ		0,43	4,5

Завдання для розрахунку

При виконанні розрахункової роботи необхідно знайти:

1. У заданій точці К₁₆ електричної схеми (рис. 1) аналітичним методом визначити:

- початкове значення періодичної складової струму трифазного короткого замикання;

- миттєве значення аперіодичної складової струму трифазного короткого замикання;

- значення ударного струму;

- діюче значення струму за перший період;

2. Використовуючи метод розрахункових кривих у зазначеній крапці К₁₆ визначити значення періодичної складової струму для моментів часу t = 0 с,
t = 0,2 с і t = ∞ при:

- трифазному короткому замиканні;

- однофазному короткому замиканні.

ЗМІСТ

ВСТУП

1. Визначення початкового значення періодичної складової струму трифазного короткого замикання (КЗ) у заданій точці схеми аналітичним методом. Розрахунок миттєвого значення аперіодичної складової струму, значення ударного струму і діючого значення струму за перший період

1.1 Складання еквівалентної схеми заміщення і розрахунок
параметрів її елементів

1.2 Згортання схеми заміщення щодо точки КЗ

1.3 Визначення початкового значення періодичної складової струму
трифазного КЗ у заданій точці

1.4 Розрахунок миттєвого значення аперіодичної складової струму

1.4.1 Розрахунок еквівалентних індуктивних опорів кожної з груп
елементів

1.4.2 Розрахунок еквівалентних активних опорів кожної з груп
елементів

1.4.3 Визначення постійних часу загасання аперіодичних
складових струмів КЗ

1.4.4 Розрахунок миттєвого значення аперіодичної складової
струму в точці КЗ для будь-якого моменту часу

1.5 Розрахунок значення ударного струму КЗ

1.6 Розрахунок діючого значення струму КЗ за перший період

2. Використання методу розрахункових кривих для визначення значення періодичної складової струму у зазначеній крапці К₁₆ для різних моментів часу при трифазному КЗ

2.1 Складання еквівалентної схеми заміщення і розрахунок
параметрів її елементів

2.2 Згортання схеми заміщення щодо точки КЗ

2.3 Визначення значення періодичної складової струму трифазного
КЗ у заданій точці для різних моментів часу

3. Використання методу розрахункових кривих для визначення значення періодичної складової струму у зазначеній крапці К₁₆ для різних моментів часу при однофазному КЗ

3.1 Складання еквівалентної схеми заміщення і розрахунок
параметрів її елементів

3.1.1 Складання схеми заміщення прямої послідовності і її
згортання до найпростішого вигляду

3.1.2 Складання схеми заміщення зворотної послідовності і її
згортання до найпростішого вигляду

3.1.3 Складання схеми заміщення нульової послідовності і її
згортання до найпростішого вигляду

3.2 Розрахунок значень періодичної складової струму прямої
послідовності особливої фази для різних моментів часу

3.3 Визначення фазної величини періодичної складової струму
пошкодженої фази в місці однофазного КЗ для різних моментів
часу

3.4 Визначення симетричних складових і побудова векторних діаграм
струмів і напруг однофазного КЗ для окремого випадку при t = 0 с

ВИСНОВОК

ЛІТЕРАТУРА

ВСТУП

Перехідні процеси відбуваються в системах електропостачання як в умовах нормальної експлуатації, так і в аварійних умовах. При будь-якому перехідному процесі здійснюється зміна електромагнітного стану системи і порушення балансу між електромагнітною потужністю і потужністю на валу машин, які обертаються, що спричиняє відповідну зміну швидкості обертання машин до певного моменту, який визначається наявністю і функціональними можливостями засобів регулювання і повернення системи в нормальний стан.

Таким чином, будь-який перехідний процес характеризується сукупністю електромеханічних і електромагнітних змін у системах, які взаємопов’язані між собою спільністю фізичних явищ.

Найбільш розповсюдженими перехідними процесами в електричній системі є процеси, викликані включенням і відключенням двигунів і інших приймачів електроенергії, коротким замиканням, а також повторним включенням і відключенням (одночасним чи каскадним) короткозамкнутих ланцюгів; виникненням місцевої несиметрії в системі (наприклад, відключенням тільки однієї чи двох фаз); дією форсування руху синхронних машин, а також їхнього розбудження (тобто гасінням їхніх магнітних полів); несинхронним включенням синхронних генераторів.

Основною причиною виникнення електромагнітних перехідних процесів є коротке замикання.

Розрахунок електромагнітного перехідного процесу в сучасній електричній системі, з урахуванням всіх умов і факторів, складний і громіздкий. Тому для спрощення задачі і додання їй практичної можливості вводиться ряд допущень. Останні залежать від характеру і постановки самої задачі, не повинні робити істотного впливу на кінцевий результат.

Розрахунок електромагнітних перехідних процесів, обумовлених короткими замиканнями, можна робити в іменованій і відносній системах одиниць. Представлення будь-яких фізичних величин (струмів, опорів, потокощеплень, потужностей, напруг і т.д.) у відносній, безрозмірній системі одиниць дозволяє спростити деякі теоретичні викладення і додати їм більш загальний характер. У практичних розрахунках таке представлення величин додає результатам велику наочність і дає можливість швидше орієнтуватися в порядку обумовлених значень. Завдяки цьому багатоступінчасті, складні, розгалужені схеми електричних високовольтних систем доцільно розраховувати у відносній системі одиниць.

При наявності схем з довільним числом всіляких елементів як одиниці виміру встановлюються базисні умови, зручні для виробленого розрахунку, наприклад, базисний струм і базисна потужність, чи базисна напруга і базисна потужність, чи базисний опір і базисний струм. Дві інші базисні одиниці (умови) одержують шляхом перерахунку.

Будь-яку схему електричної системи при наявності трансформаторів і автотрансформаторів для розрахунку струмів короткого замикання необхідно представити схемою заміщення. Скласти схему заміщення – це значить замінити всі магнітозв’язані ланцюги одним еквівалентним електрично зв'язаним ланцюгом.

Для точних розрахунків користаються точними схемами заміщення, а для інженерних практичних розрахунків, що не претендують на велику точність, – наближеними формулами приведення до схем заміщення.

Метою розрахунково-графічної роботи (РГР) є:

- допомогти зрозуміти значення перехідних процесів у створенні надійних систем електропостачання;

- зрозуміти причини виникнення і наслідки аварійних режимів у системах електропостачання;

- виявити закономірності протікання електромагнітних перехідних процесів при різних режимах систем електропостачання;

- освоїти методи розрахунку електромагнітних перехідних процесів при симетричних і несиметричних режимах;

- отримати уміння організувати безаварійну експлуатацію систем електропостачання;

- навчитися складати розрахункові схеми короткозамкнутого ланцюга і приводити параметри його елементів до базисних умов;

- навчитися визначати результуючий опір короткозамкнутого ланцюга;

- навчитися розраховувати струми короткого замикання в різних точках систем електропостачання;

- зрозуміти методику проектування систем електропостачання з обліком можливих аварійних ситуацій і виникаючих перехідних процесів;

- навчити правильно оцінювати значення струмів короткого замикання без складних розрахунків.

Розрахунки у РГР будемо виконувати з точністю до другого десяткового знака для значень >1, або до третього знака для значень <1.

1. Визначення початкового значення періодичної складової струму трифазного короткого замикання (КЗ) у заданій точці схеми аналітичним методом. Розрахунок миттєвого значення аперіодичної складової струму, значення ударного струму і діючого значення струму за перший період

1.1 Складання еквівалентної схеми заміщення і розрахунок параметрів її елементів

Кожен опір елемента схеми заміщення (рис. 1.1) позначається у вигляді дробу – у чисельнику вказують порядковий номер опору, у знаменнику – величину реактивного опору у відносних одиницях. Активні опори в схемі заміщення не враховуються, бо вони є набагато меншими за реактивні, а тому при розрахунку періодичної складової струму трифазного КЗ їми можна знехтувати.

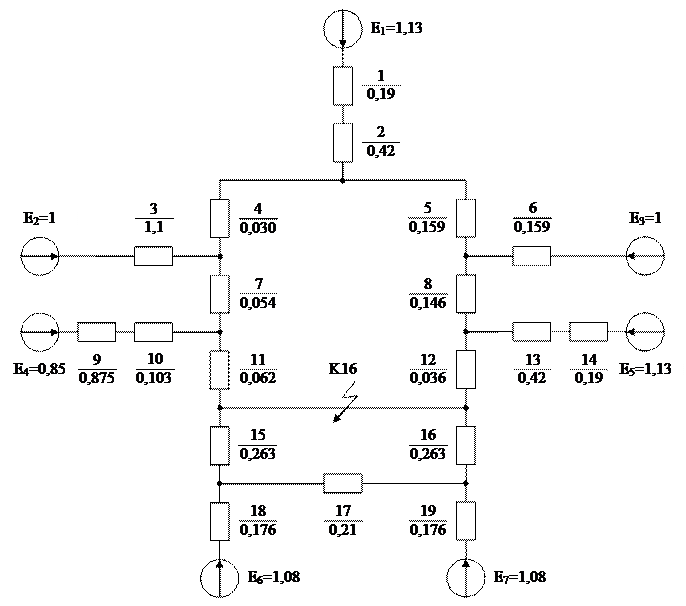
Рис. 1.1 – Еквівалентна схема заміщення розрахункової схеми для

визначення початкового значення періодичної складової

струму трифазного КЗ аналітичним методом

Розрахунок опорів (а також ЕДС для генераторів, систем і навантаження) елементів схеми заміщення проводимо у відносних одиницях за формулами наближеного приведення.

Приймаємо, що: S_б = 100 МВА; U_б = 115 кВ; U_бI = 10,5 кВ; U_бII = 115 кВ,

де U_бI, U_бII, U_б – базисні напруги на відповідних ступенях трансформації і у точці КЗ.

Активні опори елементів визначаємо заздалегідь (для п. 1.4) за формулою:

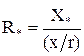
де x/r – визначається за табл. 7.1 [1].

- для генераторів:

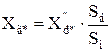
Генератори Г-1, Г-2:

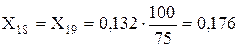
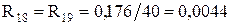
За таблицею 3.1 [1] визначаємо значення E^’’ генератора у відносних одиницях:

E₆ = E₇ = 1,08

Генератори Г-3, Г-4:

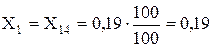
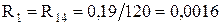
E₁ = E₅ = 1,13 (за табл. 3.1 [1])

- для трансформаторів:

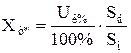
Трансформатори Т-1, Т-2:

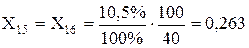
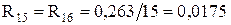
Трансформатори Т-3, Т-4:

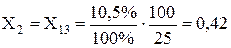
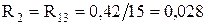
Трансформатори Т-5, Т-7:

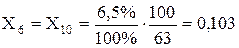
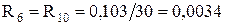
Трансформатор Т-6:

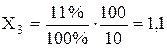
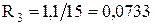
- для реакторів:

,

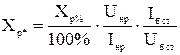де I_{б ст}, U_{б ст} – відповідно струм і напруга ступені де встановлено реактор.

Реактор Р-1:

,

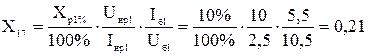де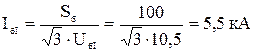

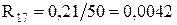
- для узагальненого навантаження:

,

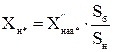де 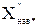= 0,35 (за табл. 3.1 [1]).

Навантаження Н-1:

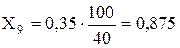
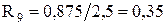
E₄ = 0,85 (за табл. 3.1 [1])

- для систем нескінченної потужності:

;

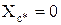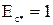
Системи С-1, С-2:

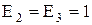
- для ліній електропередачі:

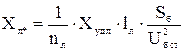
де n_л – кількість паралельних ліній електропередачі.

Лінія Л-1:

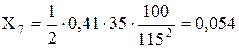
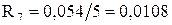
Лінія Л-2:

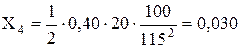
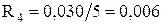
Лінія Л-3:

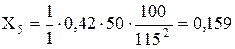
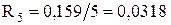
Лінія Л-4:

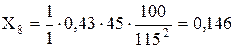
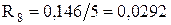
Лінія Л-5:

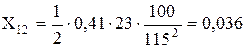
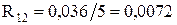
Лінія Л-6:

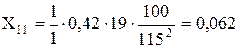
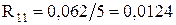
1.2 Згортання схеми заміщення (рис. 1.1) щодо точки КЗ

І-ий етап (рис 1.2):

Об’єднуємо послідовно з’єднані опори:

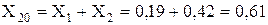
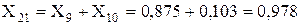
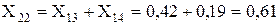
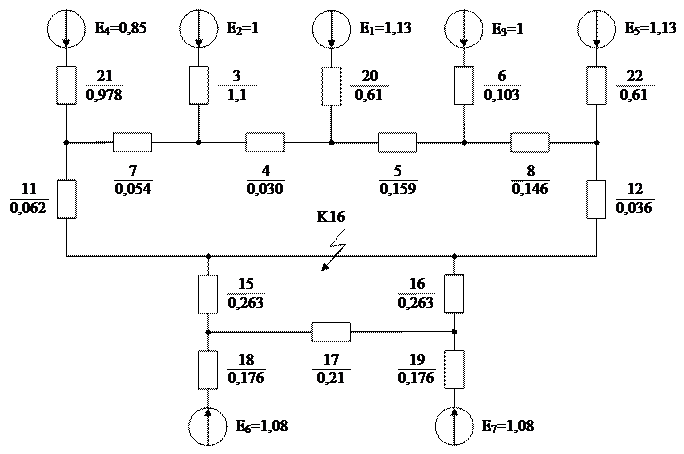
Рис. 1.2 – І-ий етап перетворення

ІІ-ий етап (рис 1.3):

Розглянемо гілки генераторів Г-1 і Г-2 до точки КЗ. Оскільки X₁₈ = X₁₉,
X₁₅ = X₁₆ і Е₆ = Е₇, то реактор підключений до зажимів з однаковими потенціалами, а гілки генераторів Г-1 і Г-2 можна вважати паралельно підімкненими до точки КЗ. Тоді їх можна об’єднати і розрахувати їхній еквівалентний опір і ЕДС:

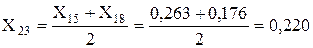
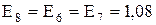
Перетворюємо зірку опорів X₂₁, X₇, X₁₁ у еквівалентний трикутник X₂₄, X₂₅, X₂₆:

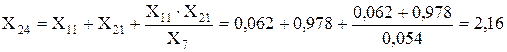
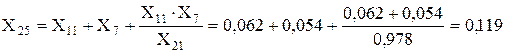
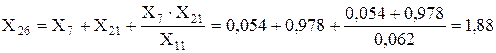
Опори X₂₄ і X₂₆ розділяємо в точці з’єднання і разом з Е₄ переносимо у новоутворені незалежні гілки.

Перетворюємо зірку опорів X₈, X₂₂, X₁₂ у еквівалентний трикутник X₂₇, X₂₈, X₂₉ (за попередньою методикою):

X₂₇ = 0,191; X₂₈ = 3,23; X₂₉ = 0,796

Опори X₂₈ і X₂₉ розділяємо в точці з’єднання і разом з Е₅ переносимо у новоутворені незалежні гілки.

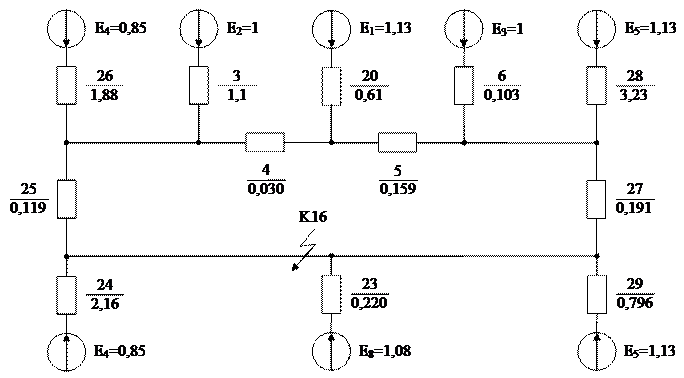
Рис. 1.3 – ІІ-ий етап перетворення

ІІІ-ій етап (рис 1.4):

Об’єднуємо паралельні гілки з X₂₆ і X₃ і розраховуємо їхній еквівалентний опір і ЕДС:

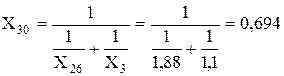
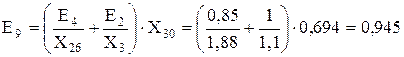
Об’єднуємо паралельні гілки з X₆ і X₂₈, розраховуємо їхній еквівалентний опір і ЕДС (за попередньою методикою):

;

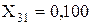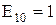
Об’єднуємо паралельні гілки з X_24, X₂₃ і X₂₉, розраховуємо їхній еквівалентний опір і ЕДС:

;

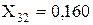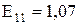
Рис. 1.4 – ІІІ-ій етап перетворення

IV-ий етап (рис 1.5):

Рис. 1.5 – IV-ий етап перетворення

Перетворюємо зірку опорів X₃₀, X₄, X₂₅ у еквівалентний трикутник:

X₃₃ = 3,57; X₃₄ = 0,154; X₃₅ = 0,899

Опори X₃₃ і X₃₅ розділяємо в точці з’єднання і разом з Е₉ переносимо у новоутворені незалежні гілки.

Перетворюємо зірку опорів X₃₁, X₅, X₂₇ у еквівалентний трикутник:

X₃₆ = 0,411; X₃₇ = 0,654; X₃₈ = 0,342

Опори X₃₆ і X₃₈ розділяємо в точці з’єднання і разом з Е₁₀ переносимо у новоутворені незалежні гілки.

V-ий етап (рис 1.6):

Об’єднуємо паралельні гілки з X_35, X₂₀ і X₃₈, розраховуємо їхній еквівалентний опір і ЕДС:

;

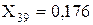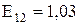
Об’єднуємо паралельні гілки з X_33, X₃₂ і X₃₆, розраховуємо їхній еквівалентний опір і ЕДС:

;

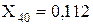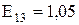
Перетворюємо послідовно-паралельне з’єднання елементів X_39, X₃₄ і X₃₇:

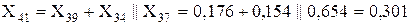
Об’єднуємо паралельні гілки з X₄₀ і X₄₁, розраховуємо їхній еквівалентний опір і ЕДС:

;

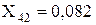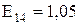
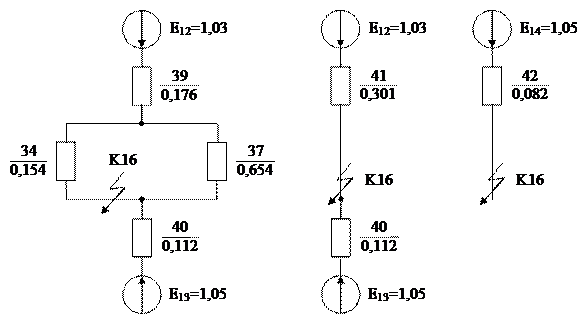
Рис. 1.6 – IV-ий етап перетворення

1.3 Визначення початкового значення періодичної складової струму трифазного КЗ у заданій точці:

,

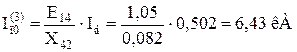де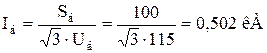

1.4 Розрахунок миттєвого значення аперіодичної складової струму

Найбільше початкове значення аперіодичної складової струму КЗ у загальному випадку варто приймати рівним амплітуді періодичної складової струму в початковий момент КЗ.

Оскільки джерела електроенергії і споживачі знаходяться в різних умовах щодо місця КЗ, то необхідно перетворити схему заміщення до багатопроменевого вигляду. У нашому випадку досить виділити дві групи елементів. До першої групи відносимо більш віддалені від точки КЗ елементи, тобто генератори Г-3 і Г-4, системи С-1 і С-2, а також навантаження Н-1. До другої групи відносимо гілки генераторів Г-1 і Г-2.

1.4.1 Розрахунок еквівалентних індуктивних опорів кожної з груп елементів

Вихідною схемою заміщення для визначення еквівалентних індуктивних опорів є схема наведена на рис 1.1. Згортання схеми заміщення повністю повторює п. 1.2. Кінцева схема після спрощення наведена на центральному малюнку рис. 1.6.

Еквівалентні реактивні опори кожної з гілок рівні:

;

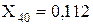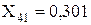
1.4.2 Розрахунок еквівалентних активних опорів кожної з груп елементів

Вихідною схемою заміщення для визначення еквівалентних активних опорів є схема наведена на рис. 1.7. На ній усі елементи розрахункової схеми враховуються лише своїми активними опорами (розраховані у п. 1.1). ЕДС елементів при побудові схеми не вказується.

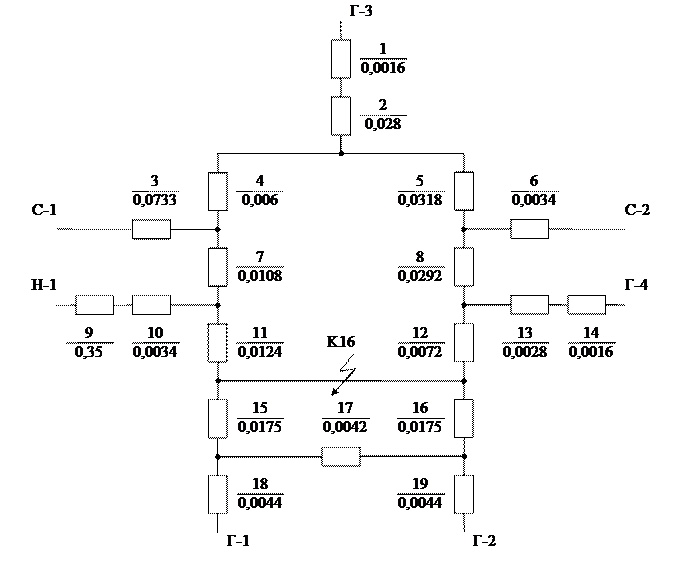
Рис. 1.7 – Вихідна схема заміщення для визначення еквівалентних активних опорів

Згортання схеми заміщення проводимо згідно методики описаній у п. 1.2. Проміжні схеми заміщення не наводимо, враховуючи, що за конфігурацією і нумерацією елементів вони відповідають схемам наведеним на рис. 1.2 – рис. 1.6.

При згортанні схеми заміщення отримуємо такі значення активних опорів:

І-ий етап: ; ;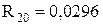

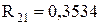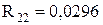
ІІ-ий етап: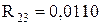

; ;

; ;

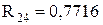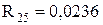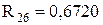
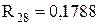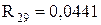
ІІІ-ій етап: ; ;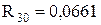

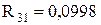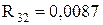
IV-ий етап: ; ;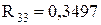

; ;

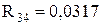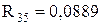
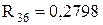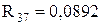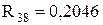
V-ий етап: ; ;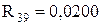

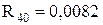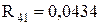
Схема заміщення, згорнута до двопроменевого виду, наведена на рис. 1.8.

Рис. 1.8 – Схема заміщення, згорнута до двопроменевого виду

Еквівалентні активні опори кожної з гілок рівні:

;

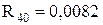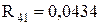
1.4.3 Визначення постійних часу загасання аперіодичних складових струмів КЗ:

;

,

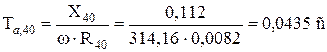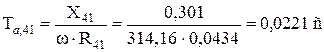де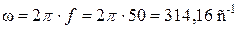

1.4.4 Розрахунок миттєвого значення аперіодичної складової струму в точці КЗ для будь-якого моменту часу:

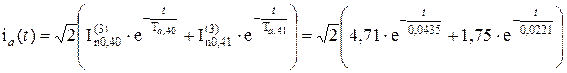
де 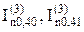– початкові значення періодичної складової струмів, що течуть через опори X₄₀ і X₄₁, при трифазному КЗ:

;

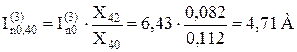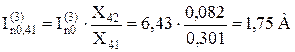
1.5 Розрахунок значення ударного струму КЗ

,

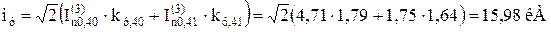де 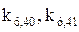– ударні коефіцієнти у кожному з променів:

;

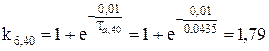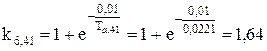
1.6 Розрахунок діючого значення струму КЗ за перший період

,

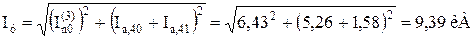де 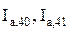– діючі значення аперіодичної складової струмів КЗ кожної з гілок:

;

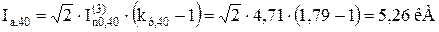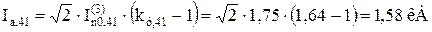
2. Використання методу розрахункових кривих для визначення значення періодичної складової струму у зазначеній крапці К₁₆ для різних моментів часу при трифазному КЗ

2.1 Складання еквівалентної схеми заміщення і розрахунок параметрів її елементів

Схему заміщення будуємо виходячи зі схеми рис. 1.1, враховуючи такі положення:

- навантаження у схему заміщення не вводиться, бо воно враховується методикою розрахунку;

- ЕДС генераторів і систем у схемі заміщення не вказуються, але згідно методики розрахунку всі ЕДС приймаються рівними 1 в.о..

Опори елементів схеми заміщення розраховані у п. 1.1.

Еквівалентна схема заміщення, побудована з урахуванням необхідних положень наведена на рис. 2.1.

Рис. 2.1 – Еквівалентна схема заміщення розрахункової схеми для

визначення значень періодичної складової струму трифазного

КЗ у будь-який момент часу методом розрахункових кривих

2.2 Згортання схеми заміщення (рис. 2.1) щодо точки КЗ

І-ий етап (рис 2.2):

Перетворюємо послідовно підключені опори X₇ і X₁₁:

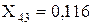
Проводимо перетворення паралельних гілок генераторів Г-1 і Г-2 згідно п. 1.2 (ІІ-ий етап).

Приймаємо допущення, що генератор Г-3 працює далеко від точки КЗ (віддалене КЗ) і аварійні струми не впливають на зміну напруги на його затискачах. Тоді його можна прийняти схожим за роботою до систем С-1 і С-2 і об’єднати їх разом.

Перетворюємо трикутник опорів X₃, X₄, X₂₀ у еквівалентну зірку:

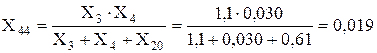
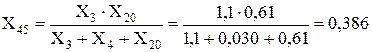
Враховуючи, що ЕДС приймаються рівними 1 в.о., то можна вважати С-1 і Г-3, після перетворення у зірку, об’єднаними.

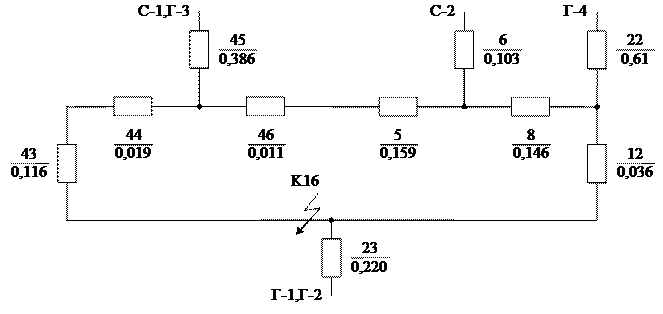
Рис. 2.2 – І-ий етап перетворення

ІІ-ий етап (рис 2.3):

Рис. 2.3 – ІІ-ий етап перетворення

Перетворюємо послідовно підключені опори X₄₃ і X₄₄:

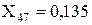
Перетворюємо послідовно підключені опори X₄₆ і X₅:

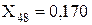
ІІІ-ій етап (рис 2.4):

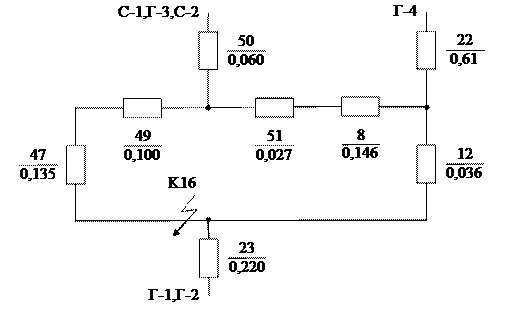
Рис. 2.4 – ІІІ-ій етап перетворення

Перетворюємо трикутник опорів X₄₅, X₄₈, X₆ у еквівалентну зірку:

; ;

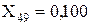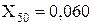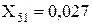
Враховуючи, що ЕДС приймаються рівними 1 в.о., то можна вважати С-1, Г-3 і С-2 об’єднаними.

ІV-ий етап (рис 2.5):

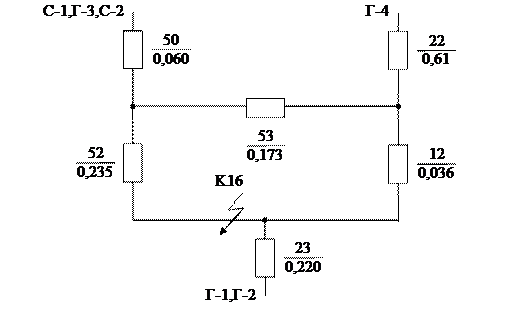
Рис. 2.5 – ІV-ий етап перетворення

Перетворюємо послідовно підключені опори X₄₇ і X₄₉:

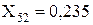
Перетворюємо послідовно підключені опори X₅₁ і X₈:

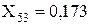
V-ий етап (рис 2.6):

Перетворюємо трикутник опорів X₅₂, X₅₃, X₁₂ у еквівалентну зірку:

; ;

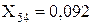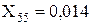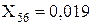
Рис. 2.6 – V-ий етап перетвореня

VІ-ий етап (рис 2.7):

Рис. 2.7 –VІ-ий етап перетворення

Перетворюємо послідовно підключені опори X₅₄ і X₅₀:

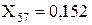
Перетворюємо послідовно підключені опори X₅₅ і X₂₂:

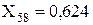
Струми від гілок з опорами X₅₇ і X₅₈ проходять через загальний опір X₅₆. Щоб перетворити схему до променевого вигляду (рис. 2.7 справа), необхідно скористатися коефіцієнтами струморозподілу:

Результуючі опори променів у цьому випадку визначають за формулами:

;

,

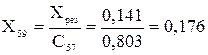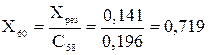де X_рез – результуючий опір схеми відносно точки КЗ:

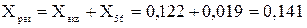
X_екв – еквівалентний опір паралельного з’єднання:

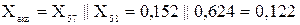
С₅₇, С₅₈ – коефіцієнти струморозподілу кожної з гілок:

;

.

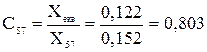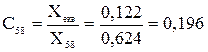2.3 Визначення значення періодичної складової струму трифазного КЗ у заданій точці для різних моментів часу

Для об’єднаної гілки С-1,Г-3,С-2 значення періодичної складової струму для будь-якого моменту часу визначається:

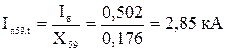
Для гілок Г-4 і Г-1,Г-2 значення періодичної складової струму для будь-якого моменту часу визначається за розрахунковими кривими.

Приводимо отримані результуючі значення опорів гілок до номінальних умов, тобто визначаємо розрахункові опори:

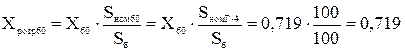
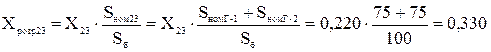
За розрахунковими кривими для типових турбогенераторів з АРЗ (рис. 5.5 [2]) визначаємо відносні значення періодичної складової струму КЗ від кожного джерела для відповідних моментів часу (t = 0 с; t = 0,2 с; t → ∞):

Для гілки Г-4:

; ;

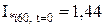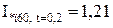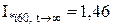
Для гілки Г-1,Г-2:

; ;

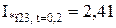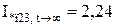
Обчислюємо значення періодичної складової струму КЗ у іменованих одиницях від кожного джерела для відповідних моментів часу:

Для гілки Г-4:

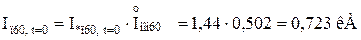
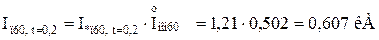
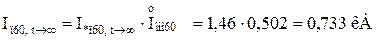
Для гілки Г-1,Г-2:

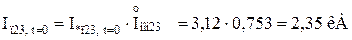
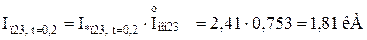
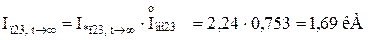
де 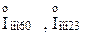– сумарний номінальний струм генераторів, приведений до ступені КЗ:

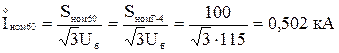
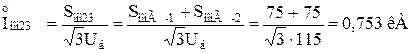
Визначаємо періодичну складову струму в точці КЗ в задані моменти часу:

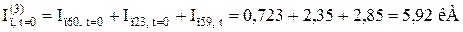
(порівнюємо з аналітичним методом: )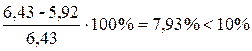

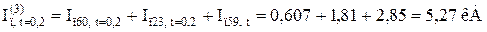
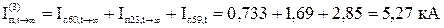
3. Використання методу розрахункових кривих для визначення значення періодичної складової струму у зазначеній крапці К₁₆ для різних моментів часу при однофазному КЗ

3.1 Складання еквівалентної схеми заміщення і розрахунок параметрів її елементів

При розрахунку несиметричного КЗ застосовують метод симетричних складових, згідно якому для розрахунку однофазного струму КЗ необхідно скласти схеми заміщення прямої, зворотної і нульової послідовностей.

3.1.1 Складання схеми заміщення прямої послідовності і її згортання до найпростішого вигляду

Схема заміщення прямої послідовності по конфігурації й опорам елементів цілком відповідає схемі при трифазному КЗ наведеній на рис. 2.1.

Згортання схеми заміщення прямої послідовності до найпростішого вигляду повністю повторює перетворення і розрахунки наведені у п. 2.2.

Схема заміщення прямої послідовності після згортання наведена на рис. 3.1 (усі ЕДС на схемі приймаються рівними 1 в.о.).

Рис. 3.1 – Схема заміщення прямої послідовності після

згортання до найпростішого вигляду

3.1.2 Складання схеми заміщення зворотної послідовності і її згортання до найпростішого вигляду

Якщо прийняти допущення, що реактивні опори генераторів з демпферною обмоткою у схемі заміщення зворотної послідовності рівні опорам генераторів у схемі прямої послідовності, то по конфігурації й опорам елементів схема заміщення зворотної послідовності цілком відповідає схемі при трифазному КЗ наведеній на рис. 1.1 (без урахування ЕДС).

Згортання схеми заміщення зворотної послідовності до найпростішого вигляду повністю повторює перетворення і розрахунки наведені у п. 1.2.

Схема заміщення зворотної послідовності після згортання наведена на рис. 3.2.

Рис. 3.2 – Схема заміщення зворотної послідовності після

згортання до найпростішого вигляду

3.1.3 Складання схеми заміщення нульової послідовності і її згортання до найпростішого вигляду

Схема заміщення нульової послідовності суттєво відрізняється від схем прямої і зворотної послідовностей, оскільки і сама система струмів нульової послідовності інша.

Складання схеми заміщення нульової послідовності починаємо від точки КЗ і далі послідовно рухаємося до джерел (генераторів, систем, навантаження), враховуючи схеми з’єднання обмоток трансформаторів. Схема заміщення нульової послідовності наведена на рис. 3.3.

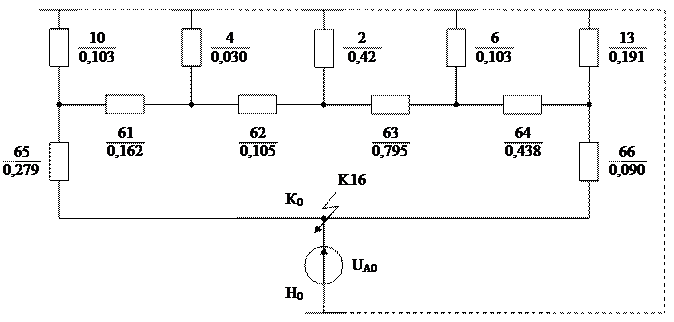
Рис. 3.3 – Схема заміщення нульової послідовності

Проведемо розрахунок опорів елементів схеми заміщення нульової послідовності:

Для ліній електропередачі:

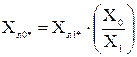
де X_л1* – реактивний опір лінії у схемі прямої послідовності.

Лінія Л-1: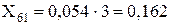

Лінія Л-2: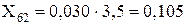

Лінія Л-3: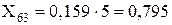

Лінія Л-4: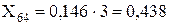

Лінія Л-5: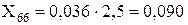

Лінія Л-6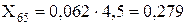

У трансформаторів Т-4, Т-5, Т-6 і Т-7 обмотки високої напруги з’єднані у зірку з заземленою нейтраллю, а обмотки низької напруги з’єднані у трикутник. Тому до схеми заміщення нульової послідовності потрапляють лише опори самих трансформаторів, розраховані у п. 1.1.

У трансформаторів Т-1 і Т-2 обмотки високої напруги з’єднані у трикутник, тому опори цих трансформаторів для струмів нульової послідовності будуть рівними нескінченності, і у схемі заміщення нульової послідовності вони не враховуються разом із більш віддаленими елементами (Г-1, Г-2, Р-1).

Згортання схеми заміщення нульової послідовності до найпростішого вигляду проводимо у декілька етапів:

І-ий етап (рис 3.4):

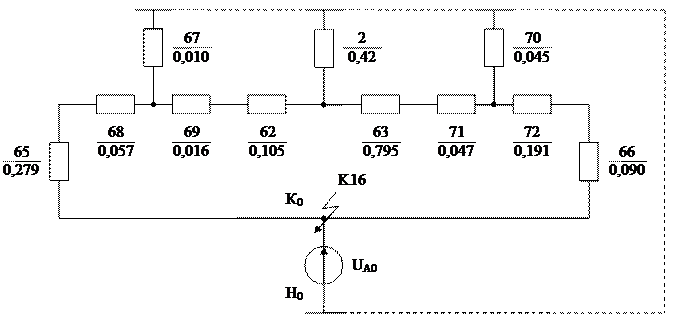
Рис. 3.4 – І-ий етап перетворення

Перетворюємо трикутник опорів X₁₀, X₄, X₆₁ у еквівалентну зірку:

; ;

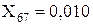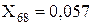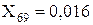
Перетворюємо трикутник опорів X₆, X₁₃, X₆₄ у еквівалентну зірку:

; ;

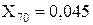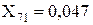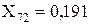
ІІ-ий етап (рис 3.5):

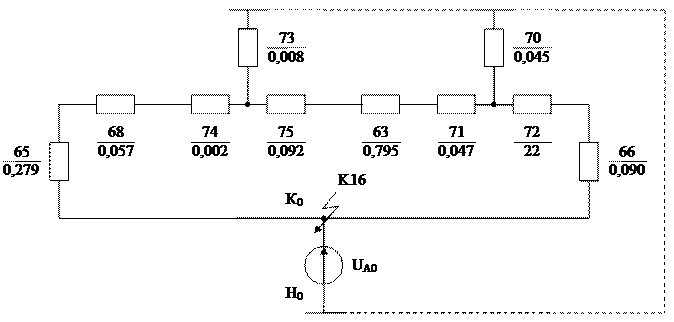
Рис. 3.5 – ІІ-ий етап перетворення

Перетворюємо трикутник опорів X₆₇, X₆₉+X₆₂, X₂ у еквівалентну зірку:

; ;

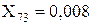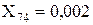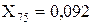
ІІІ-ій етап (рис 3.6):

Перетворюємо трикутник опорів X₇₃, X₇₅+X₆₃+X₇₁, X₇₀ у еквівалентну зірку:

; ;

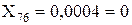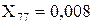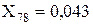
Об’єднуємо послідовно з’єднані опори:

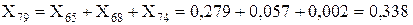
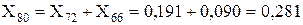
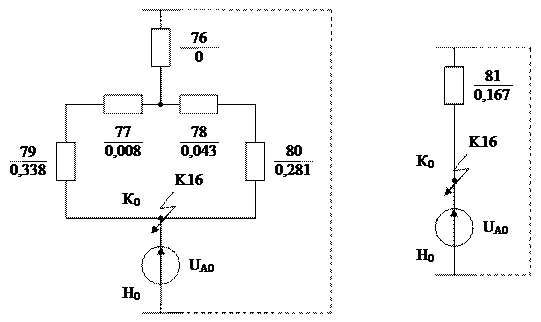
Рис. 3.6 – ІІІ-ій етап перетворення

Далі перетворюємо послідовно-паралельне з’єднання:

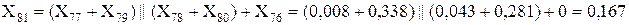
3.2 Розрахунок значень періодичної складової струму прямої послідовності особливої фази для різних моментів часу

При розрахунках струмів несиметричних КЗ застосовують правило еквівалентності, відповідно до якого струм прямої послідовності при будь-якому (n) виді несиметричного КЗ можна знайти як струм при трифазному КЗ у точці, віддаленій від дійсної точки короткого замикання на додатковий опір ∆X⁽ⁿ⁾.

Для однофазного КЗ: ∆X⁽¹⁾ = X₈₂ = X_2рез + X_0рез = X₄₂ + X₈₁ = 0,082 + 0,167 =
= 0,249

Для обчислення струму прямої послідовності особливої фази методом розрахункових кривих складаємо схему заміщення (рис. 3.7).

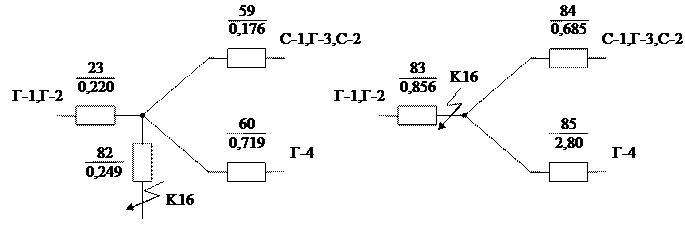
Рис. 3.7 – Схема заміщення і еквівалентна згорнута схема

для обчислення струму прямої послідовності особливої фази

методом розрахункових кривих

Струми від гілок з опорами X₂₃, X₅₉ і X₆₀ проходять через загальний опір X₆₀. Щоб перетворити схему до променевого вигляду (рис. 3.7 справа), необхідно скористатися коефіцієнтами струморозподілу:

Результуючі опори променів у цьому випадку визначають за формулами:

;

;

,

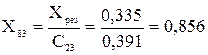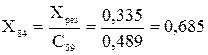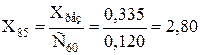де X_рез – результуючий опір схеми відносно точки КЗ:

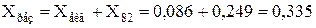
X_екв – еквівалентний опір паралельного з’єднання:

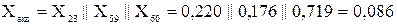
С₂₃, С₅₉, С₆₀ – коефіцієнти струморозподілу кожної з гілок:

;

;

.

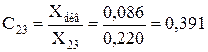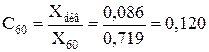Для об’єднаної гілки С-1,Г-3,С-2 значення струму прямої послідовності особливої фази для будь-якого моменту часу визначається:

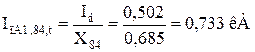
Для гілок Г-4 і Г-1,Г-2 значення періодичної складової струму прямої послідовності особливої фази для будь-якого моменту часу визначається за розрахунковими кривими.

Приводимо отримані результуючі значення опорів гілок до номінальних умов, тобто визначаємо розрахункові опори:

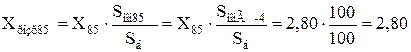
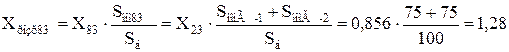
За розрахунковими кривими для типових турбогенераторів з АРЗ (додаток 1 [3]) визначаємо відносні значення періодичної складової струму прямої послідовності особливої фази від кожного джерела для відповідних моментів часу
(t = 0 с; t = 0,2 с; t → ∞):

Для гілки Г-4:

; ;

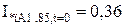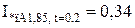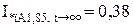
Для гілки Г-1,Г-2:

; ;

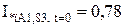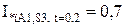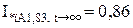
Обчислюємо значення періодичної складової струму КЗ прямої послідовності особливої фази у іменованих одиницях від кожного джерела для відповідних моментів часу:

Для гілки Г-4:

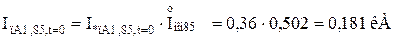
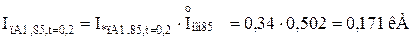
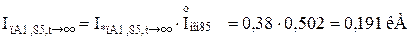
Для гілки Г-1,Г-2:

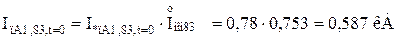
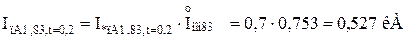
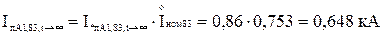
де 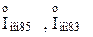– сумарний номінальний струм генераторів, приведений до ступені КЗ:

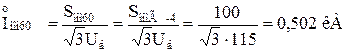
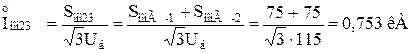
Визначаємо періодичну складову струму прямої послідовності особливої фази в точці КЗ в задані моменти часу:

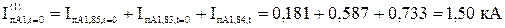
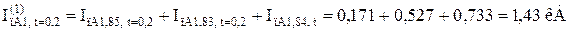
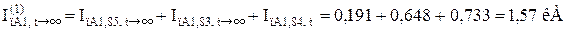
3.3 Визначення фазної величини періодичної складової струму пошкодженої фази в місці однофазного КЗ для різних моментів часу

Для однофазного КЗ величина періодичної складової струму пошкодженої фази А визначається по формулі:

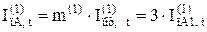
Для різних моментів часу маємо:

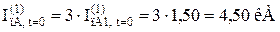
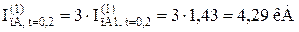
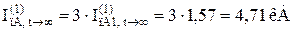
Значення періодичної складової струму у фазах B і C рівне нулю при будь-якому моменті часу: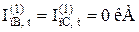

3.4 Визначення симетричних складових і побудова векторних діаграм струмів і напруг однофазного КЗ для окремого випадку при t = 0 с.

Для однофазного КЗ маємо (усі величини є комплексними числами):

- струм прямої, зворотної і нульової послідовності особливої фази:

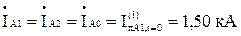
- струм фази А:

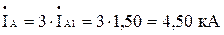
- струм фаз В і С:

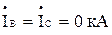
- напруга прямої послідовності особливої фази:

,

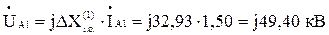де 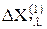– додатковий опір виражений у іменованих одиницях:

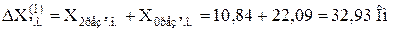
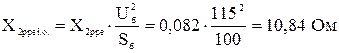
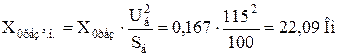
- напруга зворотної послідовності особливої фази:

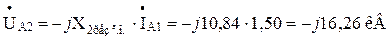
- напруга нульової послідовності особливої фази:

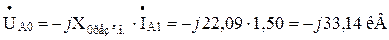
- напруга фази А:

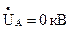
- напруга фази В:

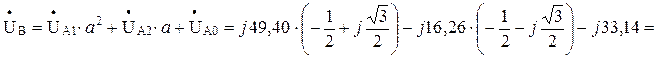
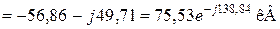
- напруга фази С:

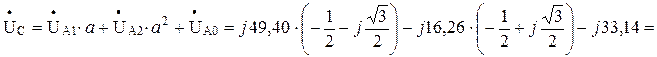
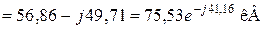
Будуємо векторну діаграму струмів у фазах (рис. 3.8) по розрахованим струмам прямої, зворотної і нульової послідовності особливої фази.

Приймаємо масштаб по струму рівний 0,5 кА/см.

З векторної діаграми знаходимо, що: 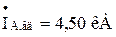; 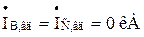, тобто значення фазних струмів повністю збігаються з розрахунковими.

Рис. 3.8 – Векторна діаграма струмів при однофазному КЗ

Будуємо векторну діаграму фазних напруг (рис. 3.9) по розрахованим фазним напругам прямої, зворотної і нульової послідовності особливої фази.

Приймаємо масштаб по напрузі рівний 10 кВ/см.

З векторної діаграми знаходимо, що:

;

;

,

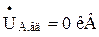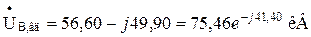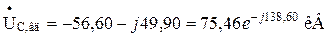тобто значення фазних напруг досить точно відповідають розрахунковим.

Рис. 3.9 – Векторна діаграма напруг при однофазному КЗ

Дата добавления: 2015-07-12