
|
Читайте также: |
Под системой уравнений внутренней баллистики принято понимать систему уравнений для наиболее сложного из трех рассматриваемых периодов - первого периода.
Система уравнений при аргументе является наиболее естественной и наглядной. Ею целесообразно пользоваться при проведении исследовании с применением ЭВМ.
Процесс горения пороха описывается уравнением
 (2.1)
(2.1)
Процесс образования пороховых газов описывается уравнением
 (2.2)
(2.2)
Процесс расширения пороховых газов описывается основным уравнением пиродинамики.
 (2.3)
(2.3)
Процесс поступательного движения снаряда описывается уравнением
 (2.4)
(2.4)
Чтобы система уравнений стала полной, добавим к этим уравнениям еще введенные ранее соотношения между переменными величинами
 (2.5)
(2.5)
 (2.6)
(2.6)
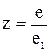 (2.7)
(2.7)
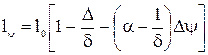 (2.8)
(2.8)
Таким образом, решая эту систему, можно выразить восемь из перечисленных переменных величин в функции от девятой величины t, принятой за аргумент.
Переменные "u" и "е" сами по себе не представляют интереса и могут быть исключены из полученной системы.
Продифференцируем по t уравнение 2.7 и заменим "dе" с помощью уравнения 2.6

Учитывая выражение 2.1 и вводя величину конечного импульса  , получим вместо двух уравнений 2.6 и 2.7 одно дифференциальное уравнение
, получим вместо двух уравнений 2.6 и 2.7 одно дифференциальное уравнение
 (2.9)
(2.9)
В результате система уравнений внутренней баллистики принимает вид
 (2.10)
(2.10)
Эта система является замкнутой и допускает единственное решение.
Отсчет времени начинается от момента начала движения снаряда, т. е. допускается, что все процессы в предварительном периоде происходят мгновенно.
При решении системы 2.10 процесс врезания снаряда в нарезы учитывается косвенно с помощью так называемого давления форсирования р0.
Будем считать, что движение снаряда начинается в момент, когда давление пороховых газов в каморе достигает величины давления форсирования р0. При этом сгорит часть пороха, определяемая величинами y0 и z0. На основании формулы пиростатики будем иметь
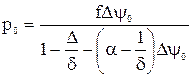
Решая это уравнение относительно y0, найдем
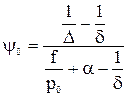 (2.11)
(2.11)
Зная величину y0, можем найти z0 на основании уравнения 2.2
 (2.12)
(2.12)
которое является квадратным уравнением относительно z0. Учитывая малость величины z0 по сравнению с единицей, в первом приближении можно пренебречь величиной lz0 и записать
 (2.13)
(2.13)
Для определения z0 во втором приближении, подставляем z0,1 в скобку правой части равенства 2.12, в результате чего получим

Или после замены z0,1 его выражением 2.13
 (2.14)
(2.14)
Начальное значение величины ly будет равно
 (2.15)
(2.15)
Таким образом, решение системы уравнений 2.10 необходимо вести при следующих начальных условиях:
при t = 0, V = 0, l=0, z = z0
Дата добавления: 2015-07-12; просмотров: 108 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| г. Послание от Божественных Основателей. | | | Материальная культура. Занятия и быт |