
Читайте также:
|
Тема 4
ОСНОВНІ ПРИНЦИПИ ПРОГНОЗУВАННЯ СТАНУ
ТЕХНІЧНИХ ОБ’ЄКТІВ
Застосування прогнозування є методичною основою для впровадження стратегії експлуатації та ремонту за зміною технічного стану авіаційної техніки.
Під прогнозом розуміється науково обґрунтоване судження про можливий стан об'єкта в майбутньому, яке базується на інформації про його поведінку у минулому, тобто передісторію його розвитку. Процес розробки прогнозів називається прогнозуванням. При вирішенні прогнозних задач розрізняють два етапи: теоретико-пізнавальний (отримання інформації про передісторію розвитку явища) та управлінський (формування управлінських рішень, які базуються на визначній тенденції розвитку об’єкта).
4.1. Часові ряди. Принципи їх використання у прогнозуванні
Практика дослідження зміни технічного стану (ТС) авіаційної техніки (АТ) полягає у вивченні динаміки його розвитку, тобто аналізу характеристик (параметрів технічного об’єкта) як функцій часу. Описання цих змін є процесом дослідження випадкових функцій, тобто функцій, значення яких у будь-які моменти часу є випадковими величинами. Випадкові функції однієї незалежної змінної, за яку, як правило, приймають час, називають випадковими процесами.
Припустимо, що у процесі дослідження випадкової функції 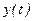 , яка є характеристикою випадкового процесу
, яка є характеристикою випадкового процесу  зміни ТС, реєстрація її значень відбувається в часі
зміни ТС, реєстрація її значень відбувається в часі 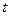 , тобто у ході дослідження значення
, тобто у ході дослідження значення  характеристики
характеристики 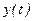 фіксується у певні моменти часу
фіксується у певні моменти часу 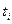 . Зібрана таким чином інформація має характер так званих панельних даних. Хронологічно організовану послідовність зафіксованих значень
. Зібрана таким чином інформація має характер так званих панельних даних. Хронологічно організовану послідовність зафіксованих значень  ,
,  величини
величини 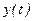 називають реалізацією цього випадкового процесу. А у статистиці така послідовність
називають реалізацією цього випадкового процесу. А у статистиці така послідовність 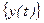 називається часовим рядом (ЧР).
називається часовим рядом (ЧР).
Ряд виду 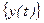 називають одномірним ЧР, оскільки дослідженню підлягає тільки одна змінна
називають одномірним ЧР, оскільки дослідженню підлягає тільки одна змінна  процесу
процесу  . Якщо виникає проблема паралельного дослідження деякої кількості змінних процесу у часі з метою знаходження закономірностей у їх взаємодії, то говорять про необхідність формування багатомірного ЧР.
. Якщо виникає проблема паралельного дослідження деякої кількості змінних процесу у часі з метою знаходження закономірностей у їх взаємодії, то говорять про необхідність формування багатомірного ЧР.
Можна зазначити, що усі задачі, зв'язані з аналізом динаміки і прогнозом зміни ТС АТ, передбачають використання як статистичної інформаційної бази ЧР тих чи інших своїх показників. Як правило, у задачах прогнозування ТС розглядаються лише дискретні (за часом спостереження) одномірні ЧР для рівновіддалених моментів 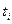 спостереження, тобто
спостереження, тобто  , де
, де  – заданий часовий такт. Такі ЧР носять назву інтервальних. Специфічність даних такого роду у авіації пов’язано з тим, що фіксація значень прогнозуючих параметрів окремих видів авіатехніки технічних ТП відбувається під час виконання окремих видів відновлювальних робіт, які є рівновіддаленими одна від іншої у часі. Окремі значення
– заданий часовий такт. Такі ЧР носять назву інтервальних. Специфічність даних такого роду у авіації пов’язано з тим, що фіксація значень прогнозуючих параметрів окремих видів авіатехніки технічних ТП відбувається під час виконання окремих видів відновлювальних робіт, які є рівновіддаленими одна від іншої у часі. Окремі значення  ЧР називаються рівнями цього ряду.
ЧР називаються рівнями цього ряду.
Основною метою статистичної обробки інформації у рамках вирішення задачі прогнозування є знаходження аналітичного виразу для зміни значення параметра прогнозування 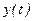 як функції часу. Особливістю такої аналітичної моделі прогнозу є те, що її можна подати сумою деякої систематичної складової і випадковими відхиленнями від її. Це знаходить своє відображення у тому, що відповідні ЧР часто подаються у виді суми:
як функції часу. Особливістю такої аналітичної моделі прогнозу є те, що її можна подати сумою деякої систематичної складової і випадковими відхиленнями від її. Це знаходить своє відображення у тому, що відповідні ЧР часто подаються у виді суми:
 (4.1)
(4.1)
де  - деяка невипадкова функція часу;
- деяка невипадкова функція часу;  - випадкова величина з нульовою середньою і дисперсією
- випадкова величина з нульовою середньою і дисперсією  . Функцію
. Функцію  , що характеризує детерміновану складову ЧР, називають трендом. Тренд характеризує основну тенденцію у напрямку розвитку процесу або його довгострокову еволюцію. Тренд є наслідком впливу на хід процесу деяких постійно діючих факторів, специфічних для нього. Випадкову складову
, що характеризує детерміновану складову ЧР, називають трендом. Тренд характеризує основну тенденцію у напрямку розвитку процесу або його довгострокову еволюцію. Тренд є наслідком впливу на хід процесу деяких постійно діючих факторів, специфічних для нього. Випадкову складову  , яка виражає відхилення рівнів ЧР від його тренду, називають випадковою компонентою. Випадкова компонента характеризує дію випадкових факторів на розвиток процесу. У загальному випадку будь-який ЧР розглядають як результуючу сукупність чотирьох компонент, а саме:
, яка виражає відхилення рівнів ЧР від його тренду, називають випадковою компонентою. Випадкова компонента характеризує дію випадкових факторів на розвиток процесу. У загальному випадку будь-який ЧР розглядають як результуючу сукупність чотирьох компонент, а саме:
1) основної тенденції – головної детермінованої компоненти;
2) періодичної компоненти, наявність якої пов'язана із впливом так званої “сезонності” розвитку процесу;
3) циклічної компоненти, яка характеризує циклічні коливання, які властиві будь-якому відтворенню процесу (наприклад, цикли, які проходять між відновленнями ТС пристроїв на ремонтних підприємствах);
4) випадкової компоненти, яка утворюється у результаті впливу на процес деякої множини випадкових факторів.
Основну тенденцію ЧР характеризує тренд. Під трендом звичайно розуміють лінію регресії, яка описує зміну значення обраного оціночного показника процесу у часі. При дослідженні часових процесів з метою прогнозування зміни їх стану першою задачею є виявлення існування у такому процесі основної тенденції. Необхідність вирішення задачі викликана тим, що не всі ЧР, які плануються для використання при розв’язку задач прогнозування розвитку процесу, містять у собі інформацію про характер зміни цього процесу. Якщо при вирішенні задачі виявлення тенденції у зміні показника отримано негативний результат, то зібрані дані не можуть бути застосовані для подальшого прогнозування стану процесу.
Не наводячи теоретичних матеріалів, які описують процедуру перевірки гіпотези про існування основної тенденції у зібраній для прогнозування інформації, припустимо, що ця тенденція у ній виявлена. Наступною задачею отримання моделі прогнозу за обраним параметром технічного пристрою є аналітичне описання основної тенденції.
4.2. Моделювання одномірних часових рядів
Результатом виявлення основної тенденції є висновок про те, що існує можливість поширити закономірності розвитку об'єкта в минулому на його майбутнє, тобто провести операцію екстраполяції. Екстраполяційні методи засновані на припущенні про те, що закон зміни, який мав місце в минулому для процесу, який досліджується, збережеться для нього і у майбутньому, тобто на факті наявності у розвитку явища основної тенденції. При дотриманні цих вимог екстраполяція здійснюється шляхом підстановки у знайдене рівняння тренда (модель  ) значення незалежної змінної
) значення незалежної змінної 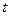 , що відповідає величині періоду упередження (прогнозу).
, що відповідає величині періоду упередження (прогнозу).
Методика екстраполяції здійснюється за таким алгоритмом:
1. Упорядкування минулих даних.
2. Згладжування ЧР.
3. Виділення тренда.
4. Визначення рівняння тренда.
5. Розрахунок прогнозного значення.
6. Оцінка довірчого інтервалу із заданою ймовірністю.
Нижче буде розглянуто методики проведення згладжування початкових даних для прогнозування – початкового ЧР та принципів визначення рівняння тренда.
4.2.1. Методи згладжування часових рядів
Згладжування часових рядів за допомогою ковзної середньої
Одним з найбільш широко відомих методів згладжування ЧР є метод ковзної середньої (МКС). Застосовуючи цей метод, можна вилучити випадкові коливання й одержати значення, які відповідають впливу головних факторів. Згладжування за допомогою ковзних середніх побудоване на тому, що в середніх величинах взаємно погашаються випадкові відхилення. Це відбувається внаслідок того, що початкові рівні ЧР замінюються середньою арифметичною величиною усередині обраного періоду часу – інтервалу згладжування  . Отримане значення відноситься до середини обраного періоду. Потім період зрушується на одне спостереження й розрахунок середньої повторюється, причому періоди визначення середньої беруться увесь час однаковими. Таким чином, у кожному випадку середня центрована, тобто віднесена до серединної точки інтервалу згладжування і являє собою рівень для цієї точки. При застосуванні МКС в розрахунках беруть участь всі рівні ряду. Чим ширшим є інтервал згладжування, тим більш плавним стає тренд. Згладжений ряд коротше початкового на
. Отримане значення відноситься до середини обраного періоду. Потім період зрушується на одне спостереження й розрахунок середньої повторюється, причому періоди визначення середньої беруться увесь час однаковими. Таким чином, у кожному випадку середня центрована, тобто віднесена до серединної точки інтервалу згладжування і являє собою рівень для цієї точки. При застосуванні МКС в розрахунках беруть участь всі рівні ряду. Чим ширшим є інтервал згладжування, тим більш плавним стає тренд. Згладжений ряд коротше початкового на  спостережень (
спостережень ( =
=  - величина інтервалу згладжування). При великих значеннях
- величина інтервалу згладжування). При великих значеннях  коливальність згладженого ряду значно знижується. Одночасно помітно скорочується кількість спостережень, що створює труднощі.
коливальність згладженого ряду значно знижується. Одночасно помітно скорочується кількість спостережень, що створює труднощі.
З вибором інтервалу згладжування пов'язане питання про кількість рівнів ряду, які беруть участь у розрахунку, і техніку цього розрахунку. Якщо число членів інтервалу згладжування непарне, то отримані за МКС значення ряду приходяться на середній член інтервалу ковзання. При парній кількості рівнів отримані значення не можна віднести до жодного рівню ряду – вони будуть розташовуватися в проміжках між рівнями.
Для першого випадку ковзна середня буде обчислюватися за формулою
 . (4.2)
. (4.2)
Для другого випадку ковзна середня визначається наступним чином:
 . (4.3)
. (4.3)
Для формул (4.2) і (4.3):  - величина
- величина  -ї ковзної середньої;
-ї ковзної середньої; 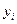 -
- 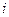 -й рівень часового ряду
-й рівень часового ряду  ;
;  - задане ціле позитивне число, за допомогою якого визначається величина інтервалу згладжування;
- задане ціле позитивне число, за допомогою якого визначається величина інтервалу згладжування;
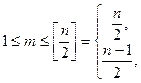




 - число рівнів часового ряду;
- число рівнів часового ряду;  - змінний індекс для інтервалу згладжування
- змінний індекс для інтервалу згладжування  .
.
Метод експоненціального згладжування(МЕЗ)
Особливість його полягає у тому, що в процедурі вирівнювання кожного спостереження використовуються тільки значення попередніх рівнів ЧР, взятих з певною вагою. Вага кожного спостереження зменшується за мірою його віддалення від моменту, для якого визначається згладжене значення. Згладжене значення рівня ряду  на момент
на момент 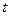 визначається за формулою
визначається за формулою
 , (4.4)
, (4.4)
де  - значення рівня ЧР, який підлягає експоненціальному згладжуванню в момент
- значення рівня ЧР, який підлягає експоненціальному згладжуванню в момент 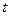 ;
;  - значення рівня ЧР для моменту
- значення рівня ЧР для моменту  , який був попередньо згладжений експоненціально;
, який був попередньо згладжений експоненціально;  - значення рівня незгладженого ЧР в момент
- значення рівня незгладженого ЧР в момент 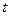 ;
;  — вага
— вага 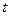 -го значення ряду динаміки (або параметр згладжування
-го значення ряду динаміки (або параметр згладжування  ).
).
З формули (4.4) видно, що при обчисленні експоненціальної середньої  використовується лише попередня експоненціальна середня
використовується лише попередня експоненціальна середня  й останнє спостереження
й останнє спостереження  , а всі попередні рівні ряду “забуваються”.
, а всі попередні рівні ряду “забуваються”.
При практичному використанні МЕЗ виникають деякі труднощі. Основними з них є вибір значення параметра згладжування  і визначення початкової умови
і визначення початкової умови  . Від чисельного значення параметра
. Від чисельного значення параметра  залежить, наскільки швидко буде зменшуватися вага попередніх спостережень і, відповідно до цього, ступінь їхнього впливу на рівень, який згладжується. Чим більше значення параметра
залежить, наскільки швидко буде зменшуватися вага попередніх спостережень і, відповідно до цього, ступінь їхнього впливу на рівень, який згладжується. Чим більше значення параметра  , тим менше позначається вплив попередніх рівнів і відповідно меншим виявляється згладжувальний вплив експоненціальної середньої. Пошук компромісного значення параметра згладжування складає задачу оптимізації моделі, яка й дотепер до кінця ще не вирішена.
, тим менше позначається вплив попередніх рівнів і відповідно меншим виявляється згладжувальний вплив експоненціальної середньої. Пошук компромісного значення параметра згладжування складає задачу оптимізації моделі, яка й дотепер до кінця ще не вирішена.
Автор методу експоненціального згладжування англійський учений Р.Г.Браун запропонував наступну формулу розрахунку  :
:
 , (4.5)
, (4.5)
де  - число рівнів, які входять в інтервал згладжування. Величина
- число рівнів, які входять в інтервал згладжування. Величина  , отже, і
, отже, і  визначаються в цьому випадку емпірично. Як практичний компроміс автор рекомендує обирати
визначаються в цьому випадку емпірично. Як практичний компроміс автор рекомендує обирати  у межах від 0,1 до 0,3.
у межах від 0,1 до 0,3.
Задачу вибору параметра  , який визначає початкові умови згладжування, пропонується вирішувати наступним чином: якщо є дані про розвиток явища в минулому, то в якості
, який визначає початкові умови згладжування, пропонується вирішувати наступним чином: якщо є дані про розвиток явища в минулому, то в якості  можна використати середню арифметичну всіх наявних рівнів ЧР або якоїсь їхньої частини, тобто
можна використати середню арифметичну всіх наявних рівнів ЧР або якоїсь їхньої частини, тобто  . Якщо ж таких відомостей немає, то в якості
. Якщо ж таких відомостей немає, то в якості  використовують вихідне (перше) значення рівня ЧР. Вага, яка приписана цьому рівню, швидко зменшується в міру віддалення від першого рівня ряду, разом із цим швидко зменшується його вплив на значення обчислених експоненціальних середніх.
використовують вихідне (перше) значення рівня ЧР. Вага, яка приписана цьому рівню, швидко зменшується в міру віддалення від першого рівня ряду, разом із цим швидко зменшується його вплив на значення обчислених експоненціальних середніх.
4.2.2. Описання рівняння тренду за допомогою методу найменших квадратів
Метод спрямований на визначення найкращої (з точки зору найменшої статистичної похибки) форми кривої  , яка апроксимує точки розкиду експериментальних даних згладженого ЧР. Існують різні прийоми, що дозволяють вибрати форму кривої, яка досить добре апроксимує ЧР. Найбільш простий шлях - це візуальний, на основі побудованого графічного зображення ЧР. За видом такого емпіричного графіка підбирається такий вид рівняння кривої, яка ближче за все підходить до емпіричних точок розкиду. Апроксимація може бути здійснена за рахунок використання:
, яка апроксимує точки розкиду експериментальних даних згладженого ЧР. Існують різні прийоми, що дозволяють вибрати форму кривої, яка досить добре апроксимує ЧР. Найбільш простий шлях - це візуальний, на основі побудованого графічного зображення ЧР. За видом такого емпіричного графіка підбирається такий вид рівняння кривої, яка ближче за все підходить до емпіричних точок розкиду. Апроксимація може бути здійснена за рахунок використання:
1) поліномів
- першого ступеню:  ; (4.6)
; (4.6)
- другого ступеню: 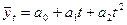 ; (4.7)
; (4.7)
- третього ступеню:  ; (4.8)
; (4.8)
-  -го ступеню:
-го ступеню:  ; (4.9)
; (4.9)
2) експонент
 ; (4.10)
; (4.10)
 ; (4.11)
; (4.11)
 ; (4.12)
; (4.12)
3) логістичних кривих
 , (4.13)
, (4.13)
де  - основа натурального логарифма;
- основа натурального логарифма;
 , (4.14)
, (4.14)
4) кривих Гомперца:  (4.15)
(4.15)
або функцій інших видів.
Параметри  та
та  наведених вище функцій мають певний якісний зміст і досить легко інтерпретуються.
наведених вище функцій мають певний якісний зміст і досить легко інтерпретуються.
Так, наприклад, рівняння прямої (поліному першого ступеню) 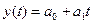 характеризує постійний приріст значень параметра прогнозування
характеризує постійний приріст значень параметра прогнозування  , рівний
, рівний 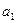 одиницям, при початковому рівні
одиницям, при початковому рівні 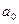 .
.
У рівнянні параболи (поліному другого степеню) 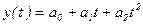 коефіцієнт
коефіцієнт 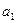 виражає початкову швидкість росту, а коефіцієнт
виражає початкову швидкість росту, а коефіцієнт 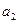 - постійну швидкість зміни приросту. Якщо рівень явища зростає із прискоренням, то величина цього прискорення в середньому за період дослідження дорівнює
- постійну швидкість зміни приросту. Якщо рівень явища зростає із прискоренням, то величина цього прискорення в середньому за період дослідження дорівнює  одиницям.
одиницям.
Експонента  відбиває постійний відносний ріст, рівний
відбиває постійний відносний ріст, рівний  одиницям, а експонента
одиницям, а експонента  характеризує постійний відносний приріст, рівний
характеризує постійний відносний приріст, рівний  одиницям.
одиницям.
На даний час у науковій літературі дано опис декількох десятків математичних функцій (кривих росту), з них найчастіше використовуються в прогнозуванні поліноміальні, експоненціальні й  -подібні криві.
-подібні криві.
Практика аналітичного моделювання свідчить про те, що існує закономірність між характером розвитку процесу, який підлягає прогнозуванню, та вибором виду функції, яка повинна описувати ці явища. Так, монотонне зростання або спадання значень показника процесу характеризують функції: лінійна, параболічна, степенева, проста експоненціальна крива, модифікована експонента або гіперболічна крива.
Для моделювання ЧР, у яких проявляється швидкий розвиток процесу на його початку і згасання у закінченні (процеси насичення) застосовуються логістичні криві.
Процеси, які характеризуються наявністю екстремальних значень показника  , описується кривою Гомперца.
, описується кривою Гомперца.
Оцінки  у формулах (4.6)-(4.9) знаходяться за методом найменших квадратів, суть якого полягає у відшуканні таких параметрів функції
у формулах (4.6)-(4.9) знаходяться за методом найменших квадратів, суть якого полягає у відшуканні таких параметрів функції  у залежності
у залежності 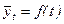 , при яких сума квадратів відхилень розрахункових значень рівнів, обчислених за цією формулою, від їхніх фактичних значень була б мінімальною.
, при яких сума квадратів відхилень розрахункових значень рівнів, обчислених за цією формулою, від їхніх фактичних значень була б мінімальною.
Вибір виду функції, що описує тренд, параметри якої визначаються методом найменших квадратів, здійснюється в більшості випадків емпірично, шляхом побудови ряду функцій і порівняння їх між собою за величиною середньоквадратичної помилки, яка обчислюється за формулою
 (4.16)
(4.16)
де  - розрахункові значення рівнів ЧР;
- розрахункові значення рівнів ЧР; 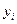 - фактичні рівні ЧР;
- фактичні рівні ЧР;  - число рівнів у ЧР;
- число рівнів у ЧР;  - число параметрів аі, які знаходяться у формулах, що описують тренд.
- число параметрів аі, які знаходяться у формулах, що описують тренд.
4.2.3. Визначення результату прогнозу
Заключним етапом процесу прогнозування є екстраполяція тенденції з використанням рівняння обраної кривої. Підставивши відповідні значення 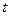 в рівняння апроксимуючої кривої, отримаємо точкові прогнози. Оскільки процеси, які досліджуються, є більшою мірою стохастичними, то імовірність того, що показник прогнозу у заданий момент часу буде дорівнювати значенню, отриманому як точковий прогноз, практично дорівнює нулю. Тому на додаток до точкового прогнозу визначають границі можливої зміни прогнозного показника - довірчі інтервали. Вони враховують невизначеність, пов'язану з обмеженим числом спостережень, їхнім відхиленням від тренда і т.д.
в рівняння апроксимуючої кривої, отримаємо точкові прогнози. Оскільки процеси, які досліджуються, є більшою мірою стохастичними, то імовірність того, що показник прогнозу у заданий момент часу буде дорівнювати значенню, отриманому як точковий прогноз, практично дорівнює нулю. Тому на додаток до точкового прогнозу визначають границі можливої зміни прогнозного показника - довірчі інтервали. Вони враховують невизначеність, пов'язану з обмеженим числом спостережень, їхнім відхиленням від тренда і т.д.
Величина довірчого інтервалу екстраполяції тренда визначається наступним чином:
 , (4.17)
, (4.17)
де  - точковий прогноз на момент
- точковий прогноз на момент 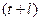 ;
;  - середня квадратична помилка тренда;
- середня квадратична помилка тренда; 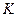 - множник, який визначається за спеціальною таблицею із заданою ймовірністю.
- множник, який визначається за спеціальною таблицею із заданою ймовірністю.
Значення Κ залежить тільки від числа спостережень (числа рівнів ряду п) і 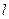 (періоду упередження). З ростом
(періоду упередження). З ростом  значення
значення 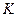 зменшуються, а з ростом
зменшуються, а з ростом 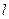 вони збільшуються. Отже, досить надійний прогноз отримуємо тоді, коли число спостережень досить велике (для лінійного тренда, наприклад, не менше 6, для параболічного - 13, для кубічного - 23) і період упередження не дуже великий. При тому самому
вони збільшуються. Отже, досить надійний прогноз отримуємо тоді, коли число спостережень досить велике (для лінійного тренда, наприклад, не менше 6, для параболічного - 13, для кубічного - 23) і період упередження не дуже великий. При тому самому  з ростом
з ростом 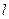 довірчий інтервал прогнозу збільшується.
довірчий інтервал прогнозу збільшується.
Довірчий інтервал прогнозу при одній і тій же величині  буде тим ширше, чим вищий ступінь полінома, який характеризує тренд.
буде тим ширше, чим вищий ступінь полінома, який характеризує тренд.
Однак до отриманих при прогнозуванні оцінках довірчих інтервалів варто відноситися з обережністю. Це пов’язано зі специфікою ЧР. Специфічність їх полягає у тому, що збільшення кількості спостережень у статичній сукупності дозволить отримати більш точні характеристики цієї сукупності, у той же час аналогічне подовження ЧР не завжди приводить до подібних результатів, особливо в тих випадках, коли ряди використовуються для прогнозування. Зазначена обставина пов'язана з тим, що інформаційна цінність рівнів втрачається в міру їхнього віддалення від періоду упередження, тобто значення рівнів ЧР при прогнозуванні нерівноцінні. Тому параметри рівнянь кривих росту не вільні від похибок і можуть змінювати свої оцінки при вилученні частини наявних членів ЧР або додаванні нових, що позначається на точності розрахункових значень рівнів.
Дата добавления: 2015-07-11; просмотров: 77 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Варіанти вихідних даних | | | ТА ЙОГО ХАРАКТЕРИСТИКИ |