Оптические свойства дисперсных систем.

Изучение оптических свойств коллоидных систем связано с практической задачей определения дисперсности или концентрации дисперсной фазы.

Как и молекулярные растворы, коллоидные системы поглощают и преломляют свет. Вместе с этим у них особенно ярко проявляется способность к светорассеиванию (опалесценции). Объясняется эта их характерная особенность соизмеримостью размеров коллоидных частиц с длинной световых волн видимой части спектра: 2r ~λ. Теория светорассеивания разработана Рэлеем. Закон Релея устанавливает зависимость интенсивности опалесценции I от размера частиц, концентрации и показателей преломления (при r < λ):

Где I₀ — интенсивность падающего света, ν — частичная концентрация (число частиц в 1м³), V — объем каждой частицы (м³), n₁ и n₀ — показатели преломления соответственно дисперсной фазы и среды, λ — длина волны падающего света.

Уравнение Релея можно записать в ином виде:

Чтобы ввести в уравнение концентрацию c, умножаем произведение νV на плотность вещества γ:

C = νVγ (кг/м³ ).

Объем частицы V в уравнение заменяем на 4/3πr³. Все постоянные величины, включая и γ, объединяются в константу К.

Отсюда следует, что отношение интенсивности рассеянного света к интенсивности падающего света, получившее название мутности и обозначающееся τ, пропорционально концентрации диспергированного вещества и радиусу его частиц. В определенной области концентраций зависимость τ = f(c) является линейной.

Одним из первых методов исследования коллоидных растворов, основанных на их опалесценции, является ультрамикроскопия. С помощью ультрамикроскопа Зигмонди можно подсчитать число частиц ν в определенном объеме доля W(берут среднее число из сотен подсчетов). Если cW — масса частиц, видимых в объеме W, то масса одной частицы равна m = принимая форму частиц за шарообразную, легко рассчитать радиус частиц r:

(м).

Если же частицы имеют форму кубика, то находят длину ребра l:

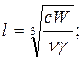
Где V— объем частицы. (В настоящее время Б.В. Дерягиным и Г.Я. Власенко разработан более точный и удобный метод поточной ультрамикроскопии, о котором уже упоминалось в разделе I.)

Светорассеяние коллоидных растворов измеряется с помощью нефелометров различных систем. В частности, нефелометрия позволяет определить концентрацию или размеры частиц дисперсной фазы. Сущность метода заключается в сравнении мутностей τ₁ и τ₂ двух систем, концентрация (или дисперсность) одной из которых известна. Освещая кюветы с золями равномерно падающим светом и меняя высоту освещенной части золей h₁ и h₂, добиваются равенства интенсивности света, рассеянного обоими золями. Тогда справедливо равенство:

τ₁h₁ = τ₂h₂,

а так как мутность τ пропорциональна концентрации с, то

c₁h₁ = c₂h₂.

Основываясь на теории Релея, Дебай предложил расчетную формулу, связывающую мутность раствора с размером его частиц

τ = HcM,

где c —концентрация(кг/м³), H— обобщенная константа, M— молекулярный или мицеллярный вес вещества. Уравнение Дебая справедливо для сильно разбавленных растворов(подробнее метод Дебая описан в гл. VII).

Опалесценцию можно наблюдать не только в боковом освещении, но также измеряя интенсивность прошедшего света.

При прохождении через систему интенсивность падающего света ослабляется вследствие поглощения или рассеяния, причем согласно закону Ламберта-Бера

I = I₀e^-εcd,

Где I— интенсивность прошедшего света, d— толщина поглощающего слоя(м), с— концентрация вещества(кг/м³), ε— индивидуальная константа, зависящая от природы вещества, длины световой волны и не зависящая от концентрации раствора.

Логарифм отношения интенсивности падающего света к интенсивности прошедшего света называется оптической плотностью системы D_λ:

Применимость закона Ламберта-Бера проверяется графически: зависимость D_λ от концентрации c должна быть линейной. Если система подчиняется этому закону, то, измерив оптическую плотность, можно по калибровочной прямой найти неизвестную концентрацию вещества.

В определенной области концентраций уравнение Ламберта-Бера применимо и к золям. Для этого одно из двух оптических явлений (опалесценция или поглощение света) должно доминировать. Примером могут служить гидрозоли кубовых и сернистых красителей, органических пигментов и т. д. — ярко окрашенных, но слабо мутных.

Наоборот: белые золи TiO₂, SiO₂, Al(OH)₃, латексы бесцветны, но мутны. В этом случае D_λ также будет расти с концентрацией линейно, что дает возможность применить оптический метод для определения концентраций золей. Для определения D_λ служат различные колориметры и фотометры.

Помимо сказанного, для белых золей Геллер установил зависимость общего вида между оптической плотностью D_λ и длинной волны:

D_λ= Kλ^-α,

Где λ — длина волны падающего света, α — коэффициент, величина которого меняется от 1 до 4 в соответствии с диаметром частиц.

Эта зависимость имеет большое практическое значение, так как позволяет по экспериментально определенным величинам D_λ при нескольких значениях λ определить размеры частиц золя. Для этого достаточно построить прямую в координатах lgD_λ = f(lgλ); тангенс угла наклона прямой равен коэффициенту α (это легко показать, прологарифмировав основное уравнение: lgD _λ= lgK-αlgλ). Далее по калибровочной кривой Геллера для латексов, построенной в координатах α = f(d), и находят средний диаметр частиц исследуемой системы.

Показатель α можно определить также по методу Теорелла: пользуясь всего двумя светофильтрами, получают два значения D_λ для двух длин волн (желательно, чтобы различия в величинах λ было возможно большим); затем, пользуясь соотношением

находят величину α. По α, как было указано, графически определяют размеры частиц.

Дата добавления: 2015-07-11