Образец выполнения типового расчета по темам

«Определенные, кратные и криволинейные интегралы»

Задание 1. Вычислить определённые интегралы:

; ; ; .

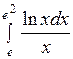Решение.

Для вычисления определённого интеграла используем формулу Ньютона-Лейбница :

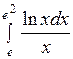
Для вычисленияиспользуем прямую подстановку .

Используем обратную подстановку . Формула замены переменной имеет вид:

Применяем формулу интегрирования по частям для определенного интеграла

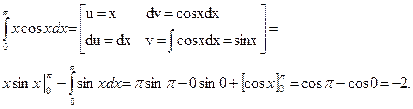
Задание 2. Вычислить несобственные интегралы или доказать их расходимость: ; .

Решение. Имеем несобственный интеграл первого рода с бесконечным верхним пределом интегрирования. Используем формулу для интегрирования: .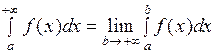

Следовательно, данный несобственный интеграл сходится.

Точка является особой точкой, поскольку подынтегральная функция имеет в ней бесконечный разрыв. Поэтому имеем несобственный интеграл второго рода. Используем формулу для интегрирования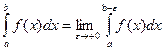

- получили бесконечный предел.

Таким образом, данный интеграл расходится.

Задание 3. Найти площадь фигуры, ограниченной линиями:

А)параболой и прямой ;

В) лемнискатой .

Решение.

А) Фигура имеет вид, изображенный на рис.

Площадь данной фигуры равна разности площадей криволинейных трапеций, образованных прямой и параболой и находится по формуле:

. Для нахождения пределов интегрирования найдём абсциссы точек пересечения графиков данных функций. Для этого решаем систему уравнений

Откуда находим , . Таким образом площадь данной фигуры равна разности площадей криволинейных трапеций, образованных прямой и параболой на отрезке .

(кв. ед.).

в ) Фигура, ограниченная лемнискатой , имеет вид

Изменению полярного угла от до соответствует четвертая часть искомой площади. Тогда по формуле находим:

(кв.ед.).

Задание 4. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:

, прямыми , и осью абсцисс.

Решение: Пользуясь формулой , находим

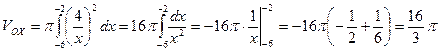(куб. ед.).

Задание 5. Вычислить длину дуги кривой , .

Решение. Пользуясь формулой , предварительно находим , откуда

Имеем

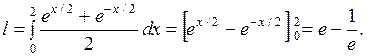
Задание 6. Изменить порядок интегрирования .

Область интегрирования изобразить на чертеже.

Решение.

1).Построение области D.

Область интегрирования D правильная в направлении оси ОY,

.

2) Для смены порядка интегрирования проецируем область D на ось ОY и получаем отрезок . Фиксируем Замечаем, что область D является сложной в направлении оси ОХ, так как точки выхода из области D лежат на линиях, которые задаются различными уравнениями: для линией выхода является парабола , для – прямая . Следовательно, область D необходимо разбить на две области () прямой .

,

3).Используя свойство аддитивности двойного интеграла по области интегрирования, имеем:

=

= .

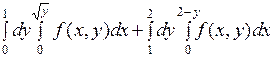Задание 7. Вычислить массу материальной пластины плотностью ,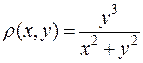

если она ограничена линиями: .

Решение.

1). Построение области D.

y

2) Массу пластины вычисляем по формуле .

Область интегрирования D – сложная в направлении оси ОY и простая в направлении оси ОХ. Поэтому для вычисления двойного интеграла переходим к вычислению повторного, у которого внутреннее интегрирование по переменной х, внешнее – по переменной y. .

3) Перейдем к вычислению повторного интеграла для определения массы: =

.

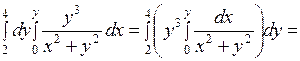
Задание 8. Вычислить площадь фигуры с помощью двойного интеграла. Условие взять из задания 3а).

Решение.

Площадь плоской области вычисляем по формуле .

Область D ограничена линиями: параболой и прямой . Область правильная в направлении оси OY, следовательно

= (кв. ед.)

Задание 9. Вычислить криволинейный интеграл

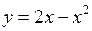, где L – дуга параболы от точки А (0,0) до точки В (2,0).

Решение.

Имеем криволинейный интеграл II рода.

Для перехода к определенному интегралу определяем пределы интегрирования: началу дуги АВ соответствует значение , концу – 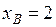. Учитывая, что 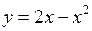и , получаем определенный интеграл:

=

.

.

Задание 10. Вычислить работу силового поля при перемещении материальной точки вдоль отрезка АВ, где А (2,1), В (1,0).

Решение.

Работу силового поля вычисляем по формуле . Имеем Уравнение прямой

АВ: 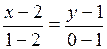, откуда , dx=d(x-1)=dx. Тогда

.

Дата добавления: 2015-07-11