Читайте также:
|
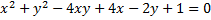
Сначала выберем такое преобразование координат, чтобы в новых координатах уравнение кривой не содержало произведения координат.
Это можно сделать, например, так. Запишем матрицу квадратичной формы
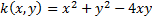
и найдём её собственные значения и собственные векторы:
, 
, 
, 
, 
,
, 
, 
;
, 
, 
.
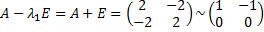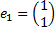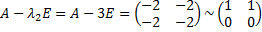Новые координатные оси направим по векторам 
и 
.
В базисе , матрица квадратичной формы имеет диагональный вид:
и, следовательно, не содержит произведения координат.
Чтобы записать формулу перехода к новым координатам, найдём орты векторов и :
, 
.
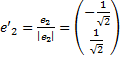Матрица перехода от исходного базиса к базису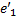 
и 
:
.
Тогда
, 
Запишем уравнение кривой в новых координатах:
.
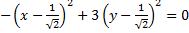Выполнив ещё одну замену переменных, перенесём начало координат 
получим:
.
Это пара пересекающихся прямых:
.
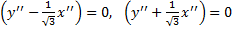Проверим.
Кривая
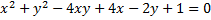
Пересекает оси координат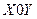 
в точках:
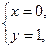
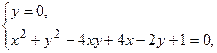
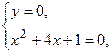
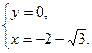
Изображенные на рисунке прямые, похоже, пересекают оси координат именно в этих точках.
Можно проверить иначе. Если преобразования выполнены правильно, то левую часть уравнения кривой можно разложить на множители.
А именно.
Уравнение 1-й прямой, проходящей через точки и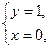 
имеет вид 
, 
.
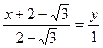Уравнение 2-й прямой, проходящей через точки 
и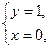
имеет вид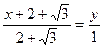 
, 
.
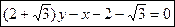Имеем: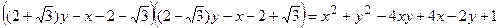 
.
Т.е. все вычисления выполнены верно.
Дата добавления: 2015-07-11; просмотров: 74 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Методология проведения контроля | | | Введение |