
|
Читайте также: |
1. Приведите примеры собственных и несобственных функций. Является ли
f(x) = 
собственной функцией? А функция h(x) = max{f(x),0}, x  R?
R?
2. Пусть f(x) – выпуклая функция, показать, что dom f – выпуклое множество.
3. Показать, что f+(x) = max{f(x),0}, x  R – является выпуклой функцией, если f(x) – выпукла на R.
R – является выпуклой функцией, если f(x) – выпукла на R.
4. Используя определение выпуклости, показать выпуклость следующих функций:
а) f(x) = |x|;
б) f(x) = 
в) f(x) = 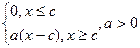
5. Пусть f(x) – выпуклая функция на выпуклом множестве Х. Показать, что множество
Ма(f)  X = {x
X = {x  X: f(x)
X: f(x)  a} выпукло для любого a
a} выпукло для любого a  Rn. Привести пример невыпуклой функции, у которой любое множество уровня является выпуклым множеством.
Rn. Привести пример невыпуклой функции, у которой любое множество уровня является выпуклым множеством.
6. Пусть gi(x), i = 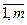 - выпуклые функции. Показать, что X = {x
- выпуклые функции. Показать, что X = {x  Rn: gi(x)
Rn: gi(x)  0, i =
0, i = 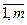 } – выпуклое множество.
} – выпуклое множество.
7. Пусть f(x) – выпуклая функция. Являются ли |f(x)| выпуклой функцией?
8. Пусть f(x) – выпуклая функция и f(x) 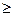 0. Показать, что g(x) = [f(X)]2 – выпуклая функция.
0. Показать, что g(x) = [f(X)]2 – выпуклая функция.
9. Доказать, что ||x|| и ||x||2, x  Rn, где ||x|| =
Rn, где ||x|| = 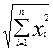 , являются выпуклыми функциями. Является ли ||x||2, x
, являются выпуклыми функциями. Является ли ||x||2, x  Rn сильно выпуклой функцией?
Rn сильно выпуклой функцией?
10. Используя определение, показать, что f(x) = ax2 + bx + c, x  R выпукла при любом а>0. Является ли эта функция сильно выпуклой?
R выпукла при любом а>0. Является ли эта функция сильно выпуклой?
11. Пусть f(x) = ||Ax – b||2, где А – заданная матрица n  m, b
m, b  Rn. Доказать, что f(x) выпукла на Rm, а если АТА – невырождена, то а) f(x) выпукла на Rm; б) f(x) сильно выпукла на Rm. Найти f ’(x), f ’’(x).
Rn. Доказать, что f(x) выпукла на Rm, а если АТА – невырождена, то а) f(x) выпукла на Rm; б) f(x) сильно выпукла на Rm. Найти f ’(x), f ’’(x).
12. Используя определение выпуклости функций, показать, что J(x(.)) = 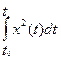 - выпуклая функция, если x(.): [t0, t1]
- выпуклая функция, если x(.): [t0, t1] 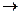 R, x(.)
R, x(.)  C([t0, t1]).
C([t0, t1]).
13. Используя критерий выпуклости дифференцируемых функций, показать, что f(x) – выпуклая функция:
a) f(x) = -lnx, x>0;
б) f(x) = eαx, α – произвольное число;
в) f(x) = x-1, x>0;
г) f(x) = xP, x 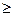 0, p
0, p 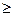 1;
1;
д) f(x) =  , x
, x  {x
{x  R2|x2>0};
R2|x2>0};
е) f(x) = 2x12 + x1x2 + x22, x  R2.
R2.
14. Показать, что если f(x) – выпуклая функция и f(x)<0 для любого х, то g(x) =  также является выпуклой.
также является выпуклой.
15.* Является ли функция f(x) = ln  , x
, x  Rn выпуклой?
Rn выпуклой?
16. Верно ли, что если f(x) – выпуклая функция на [a,b]  dom f, a, b
dom f, a, b  R, то она непрерывна на [a, b]? Верно ли, что выпуклая на (a, b)
R, то она непрерывна на [a, b]? Верно ли, что выпуклая на (a, b)  dom f, a, b
dom f, a, b  R функция является непрерывной?
R функция является непрерывной?
17. Используя неравенство Иесена и выпуклость функции g(x), доказать, что
a) 

 для xi
для xi 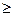 0, i =
0, i = 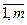 (использовать выпуклость g(x) = -lnx, x>0);
(использовать выпуклость g(x) = -lnx, x>0);
б) 
 mn-1
mn-1  , xi>0, i =
, xi>0, i = 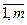 . (использовать выпуклость g(x) = xP, P
. (использовать выпуклость g(x) = xP, P 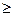 1, x
1, x 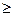 0);
0);
в) 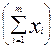

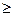 m2, xi > 0, i =
m2, xi > 0, i = 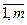 . (использовать выпуклость g(x) = x-1, x>0).
. (использовать выпуклость g(x) = x-1, x>0).
18.* Пусть  (x) непрерывна и
(x) непрерывна и  (x)
(x) 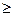 0, x
0, x  R. Доказать, что функция f(x) =
R. Доказать, что функция f(x) =  выпукла при условии, что интеграл сходится.
выпукла при условии, что интеграл сходится.
19.* Привести пример двух выпуклых функций, произведение которых невыпукло. При каких условиях произведение двух выпуклых функций выпукло? Достаточно ли для этого положительности сомножителей?
20.* Доказать, что функция f(x) выпукла на выпуклом множестве Х тогда и только тогда, когда функция g(x) = f(x + t(p –x)) одной переменной t[0, 1] выпукла при любых x, p  X, x
X, x  dom f.
dom f.
21. Проверить, является ли функция f выпуклой (вогнутой) на заданном множестве Х, или указать такие точки из Х, в окрестности которых f не является ни выпуклой, ни вогнутой.
а) f(x) = x16 + x22 + x32 + x42 + 10x1 + 5x2 – 3x4 – 20, X= R4;
б) f(x) = 6x12 + x23 + 6x32 + 12x1 – 8x2 + 7, X = {x  R3: x
R3: x 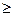 0}.
0}.
22. Выяснить, при каких значения α является выпуклыми следующие полиномы:
а) f(x) = αx12x22 + (x12 + x22);
б) f(x) = αx12x22 + (x1 + x2)4.
23. Пусть f(x) определена и выпукла на выпуклом замкнутом множестве Х. Можно ли утверждать, что
а) f(x) ограничена снизу на Х.
б) f(x) достигает своей нижней грани на множестве Х?
24. Доказать, что функция f(x) =  на [a, b] является выпуклой функцией, где
на [a, b] является выпуклой функцией, где 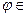 C([a, b]) и
C([a, b]) и  (t) – неубывающая функция.
(t) – неубывающая функция.
Дата добавления: 2015-09-01; просмотров: 75 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Критерии выпуклости | | | Производные по направлениям и субдифференциалы |