Точки и прямые в плоскости. Условия принадлежности

1. Прямая принадлежит плоскости, если она проведена через две точки, заведомо лежащие в этой плоскости, или проходит через одну точку и параллельна прямой, лежащей в плоскости.

2. Точка принадлежит плоскости, если она построена на прямой, принадлежащей заданной плоскости.

Построение прямых и точек в плоскости ∑ (А.В.С)

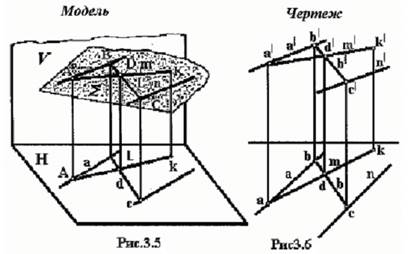
Прямая α проведена через А и Проекции a и a ´прямой а

В плоскости точки проведены через

одноименные проекции АВ

и А΄В΄ точек плоскости

По двум точкам В и С построена также прямая b(bb^|) плоскости

Прямая n проведена через точку С Проекции n и n΄ прямой

плоскости параллельно прямой α проведены через одноименные

проекции с и с΄ точки,

параллельно проекциям a и a ΄

Точка D построена на прямой b Проекции d и d΄ точки пост-

роены на одноименных проек-

циях b и b΄ прямой

Аналогично построена точка K(k΄k) плоскости на прямой m(m₁,m₂)

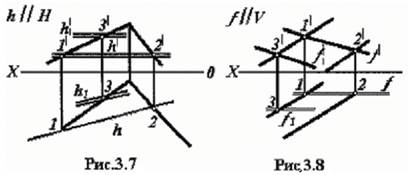
Линии уровня в плоскостях

Горизонтали плоскости Фронтали плоскости

Проецирование плоскостей частного положения

Проецирующая плоскости Плоскости уровня

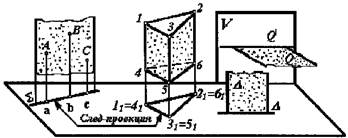
Рис. 3.9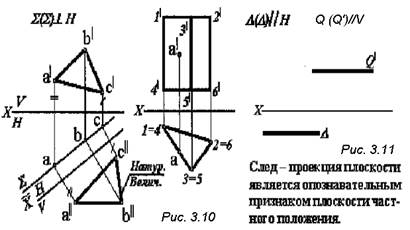

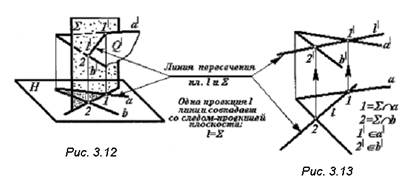
Построение линии пересечения плоскостей частного ∑(∑₁)

и общего положений Q(a∩b)

Линия пересечения плоскостей проводится через две точки 1 и 2,

одновременно принадлежащие заданным плоскостям.

Проецирование окружности, лежащей в проецирующей плоскости

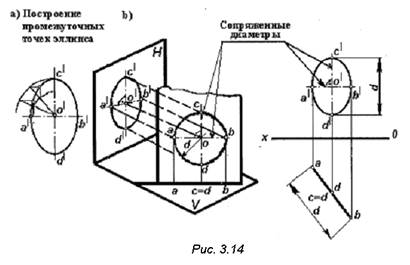
Проекциями окружности могут быть: окружность, прямая и эллипс. Для построения эллипса достаточно построить проекции двух взаимно-перпендикулярных диаметров окружности, называемых сопряженными.

Один из диаметров всегда должен быть параллельным плоскости проекций (рис. 3.14 − диаметр АВ).

Промежуточные точки эллипса строят по проекциям двух диаметров, как показано на рис. 3.14a.

Упражнения

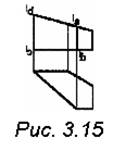6. Определите у призмы количество граней: (рис.3.15)

Всех ┴ Н
Всех ┴V
Только ┴ H
Только ┴V

Обозначьте след – проекцию грани (АВСD) и горизонтальные проекции точек А, В, С и D. Какое из рёбер призмы длиннее: АВ или CD?

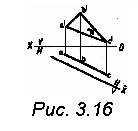
7. Выполните преобразование проекции

треугольника АВС, изменив систему

плоскостей проекции

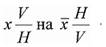
V₁//∑(ABC) и запишите величину угла

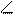треугольника при вершине В В =

Определите координаты

точки к € ∑ (АВС)

х=;у=;z= (рис.3.16)

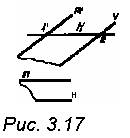
8. Построить горизонтальную

проекцию прямой h с Θ (m//n),

натуральную величину

отрезка этой прямой, заключенного

между прямыми m и n /1-2 (рис. 3.17)

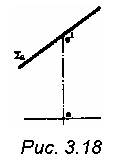
9. Построить проекции окружности,

лежащей в плоскости ∑(∑₂)_┴П₂. Центр

окружности О (О1 02), диаметр окружности

равен 40 мм. Запишите величину большой и

малой осей эллипса

А₁В₁= mm

C₁D₁= mm

(рис. 3.18)

ЗАДАЧИ

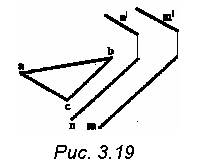11. Дано: плоскость ∑(m//n)

общего положения и проекция

А₁В₁С₁ треугольника АВС,

лежащего в этой плоскости.

Построить фронтальную

проекциюА₂В₂С₂ треугольника

(рис. 3.19)

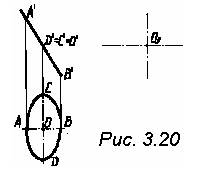12. Дано: две проекции

окружности с центром

О (Oi, 02)

Построить третью проекцию

окружности на плоскости W

(рис. 3.20)

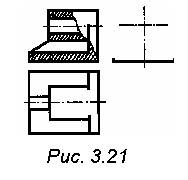
13. Дано: два изображения модели.

Построить третье изображение модели (рис. 3.21)

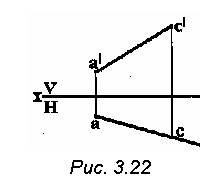14. Дано: диагональ АС (а₁с₁,a ^|c^|)

квадрата ABCD, лежащего в

горизонтально проецирующей

плоскости θ(θ₁)_┴Н

Построить проекции квадрата

(рис. 3.22).

Дата добавления: 2015-10-13