
|
Читайте также: |
У багатьох випадках для обчислення визначеного інтеграла ми не маємо можливості користуватися формулою Ньютона–Лейбніца, оскільки первісні від підінтегральних функцій не завжди можна виразити в елементарних функціях, наприклад, первісні таких функцій:
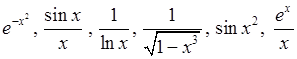 ,
,
В таких випадках (і не тільки в таких) інтеграли обчислюють наближено. Існує велика кількість так званих квадратурних формул, тобто формул для наближеного обчислення інтегралів. Познайомимось з деякими з них. Ідея їх використання полягає у тому, що графік підінтегральної функції замінюється новою лінією, більш простою, але близькою до заданої. І замість криволінійної трапеції, яку обмежено графіком функції  , ми отримуємо іншу фігуру, «близьку» до неї, але площа якої обчислюється простіше.
, ми отримуємо іншу фігуру, «близьку» до неї, але площа якої обчислюється простіше.
1. Формула прямокутників.
Нехай треба обчислити інтеграл
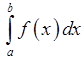 (19.1)
(19.1)
від неперервної на відрізку  функції
функції  .
.
Поділимо відрізок  на
на 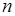 рівних частин точками
рівних частин точками 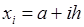 , де
, де 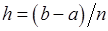 ,
, 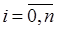 ,
, 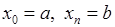 . Позначимо
. Позначимо 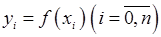 . На кожному з частинних відрізків
. На кожному з частинних відрізків 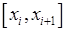 побудуємо прямокутник, основою якого є цей частинний відрізок, а висота дорівнює
побудуємо прямокутник, основою якого є цей частинний відрізок, а висота дорівнює 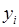 – значенню функції у лівій межі частинного відрізка (рис. 30).
– значенню функції у лівій межі частинного відрізка (рис. 30).

Рис. 30.
Площа цього прямокутника дорівнює:
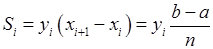 .
.
Внаслідок такої побудови дістанемо ступінчату фігуру, площа якої наближено дорівнює площі криволінійної трапеції, обмеженої графіком функції  . Таким чином площа цієї фігури і буде наближеним значенням інтеграла (16.1):
. Таким чином площа цієї фігури і буде наближеним значенням інтеграла (16.1):
 . (19.2)
. (19.2)
Формула (16.2) називається формулою лівих прямокутників.
Побудуємо тепер на кожному відрізку прямокутник, висота якого дорівнює значенню функції у правій межі відрізку 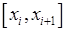 , тобто
, тобто 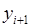 (рис. 31):
(рис. 31):
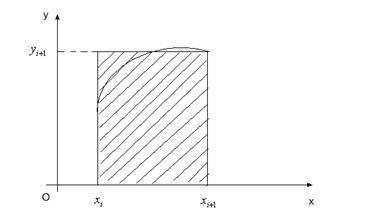 Рис. 31.
Рис. 31.
Тоді дістанемо формулу правих прямокутників:
 . (19.3)
. (19.3)
Нарешті, якщо висотами прямокутників будуть значення функції у серединах відрізків, тобто 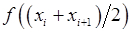 (рис. 32), то дістанемо формулу середніх прямокутників:
(рис. 32), то дістанемо формулу середніх прямокутників:
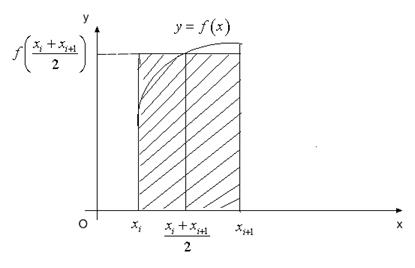
Рис. 32.
 . (19.4)
. (19.4)
2. Формула трапецій.
Замінимо тепер графік функції  ламаною лінією, з’єднавши точки з координатами
ламаною лінією, з’єднавши точки з координатами 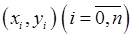 відрізками прямих (рис.31).
відрізками прямих (рис.31).
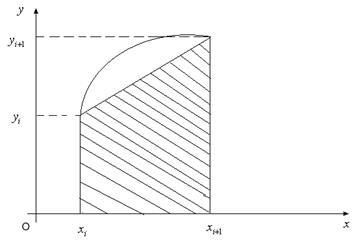
Рис. 33.
Тоді на кожному частинному відрізку буде побудовано трапецію. Площа трапеції, побудованої на відрізку  , дорівнює:
, дорівнює:
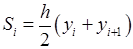 .
.
За наближене значення інтеграла (16.1) беремо суму площ всіх трапецій, тобто:
 . (19.5)
. (19.5)
Формула (16.5) називається формулою трапецій.
3. Формула парабол (Сімпсона [5]).
У формулах прямокутників і трапецій ми замінювали графік функції  відрізками прямих ліній. Щоб підвищити точність, використаємо криву лінію, наприклад, параболу.
відрізками прямих ліній. Щоб підвищити точність, використаємо криву лінію, наприклад, параболу.
Спочатку доведемо, що через три різні точки  ,
, 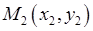 ,
, 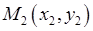 , які не лежать на одній прямій, можна провести параболу
, які не лежать на одній прямій, можна провести параболу 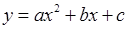 і лише одну.
і лише одну.
Дійсно, підставляючи координати точок  у рівняння параболи, дістанемо систему лінійних алгебраїчних рівнянь відносно коефіцієнтів
у рівняння параболи, дістанемо систему лінійних алгебраїчних рівнянь відносно коефіцієнтів  ,
, 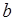 ,
, 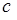 :
:
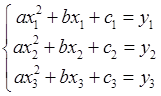 (19.6)
(19.6)
Визначник цієї системи
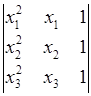
є визначником Вандермонда, і він дорівнює 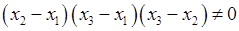 . Тому система (19.6) має єдиний розв’язок, а це означає, що коефіцієнти
. Тому система (19.6) має єдиний розв’язок, а це означає, що коефіцієнти  параболи визначаються однозначно.
параболи визначаються однозначно.
Розв’яжемо систему (16.6) для точок 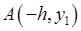 ,
,  ,
, 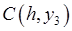 . Дістанемо:
. Дістанемо:
 .
.
Знайдемо площу 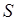 криволінійної трапеції, обмеженої параболою, що проходить через точки
криволінійної трапеції, обмеженої параболою, що проходить через точки 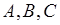 , і прямими
, і прямими  (рис. 34).
(рис. 34).
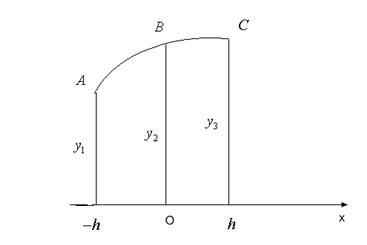
Рис. 34.

 .
.
Розглянемо тепер криволінійну трапецію, обмежену кривою  . Якщо через точки
. Якщо через точки

провести параболу, то по доведеному:
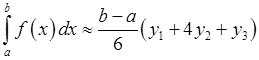 , (19.7) де
, (19.7) де 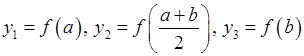 . Але якщо відрізок
. Але якщо відрізок  досить великий, то формула (19.7) буде давати значну похибку. Тоді розіб’ємо відрізок
досить великий, то формула (19.7) буде давати значну похибку. Тоді розіб’ємо відрізок  на парне число
на парне число 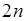 однакових частин, а криволінійну трапецію на
однакових частин, а криволінійну трапецію на 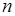 частинних криволінійних трапецій і до кожної з них застосуємо формулу (19.7).
частинних криволінійних трапецій і до кожної з них застосуємо формулу (19.7).
Додаючи почленно отримані таким чином наближені рівності, дістанемо формулу Сімпсона:

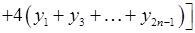 . (19.8)
. (19.8)
Можна довести, що якщо функція  має другу неперервну похідну, і
має другу неперервну похідну, і 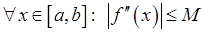 , то похибка формул (19.2) – (19.5) не перевищує величини
, то похибка формул (19.2) – (19.5) не перевищує величини
 ,
,
а похибка формули (19.8) – величини
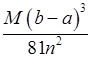 .
.
Приклади.
1. Продемонструємо спочатку застосування формул (19.2), (19.5), (19.8) на прикладі інтеграла, який обчислюється точно:

(перевірте самостійно), що наближено (з 5 знаками після коми) дорівнює 0.60948.
Розіб’ємо відрізок 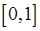 на 10 рівних частин точками
на 10 рівних частин точками 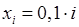
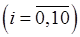 і складемо таблицю, до якої занесемо
і складемо таблицю, до якої занесемо 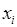 та
та 
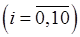 .
.
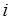
| 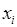
| 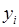
|
| 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 | 0,10050 0,20396 0,31321 0,43081 0,55902 0,69971 0,85446 1,02450 1,21083 1,41421 |
Застосування формули лівих прямокутників (19.2) дає результат:
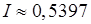 .
.
Застосування формули трапецій (19.5) дає результат:
 .
.
Застосування формули Сімпсона (19.8) дає результат:
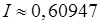 .
.
Як бачимо, з розглянутих формул найточніший результат дає формула Сімпсона.
2. Розглянемо тепер інтеграл від функції, первісна від якої не виражається в елементарних функціях:
 .
.
Розіб’ємо відрізок 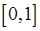 на 10 рівних частин точками
на 10 рівних частин точками 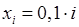
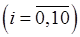 і складемо таблицю, до якої занесемо
і складемо таблицю, до якої занесемо 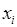 та
та 
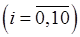 :
:
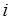
| 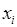
| 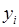
|
| 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 | 1,00005 1,00080 1,00404 1,01272 1,03078 1,06283 1,11360 1,18727 1,28690 1,41421 |
Застосування до цього інтеграла формули Сімпсона дає результат
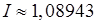 .
.
Помилка цього результату не перевищує 0,000012.
Вправи для самостійної роботи.
1. Обчислити інтеграл за допомогою формули Ньютона–Лейбніца.
1) 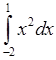 , 2)
, 2)  , 3)
, 3) 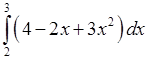 , 4)
, 4) 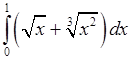 ,
,
5) 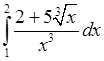 , 6)
, 6) 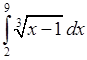 , 7)
, 7)  , 8)
, 8)  ,
,
9) 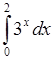 , 10)
, 10) 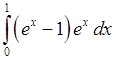 , 11)
, 11)  , 12)
, 12)  ,
,
13) 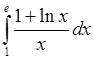 , 14)
, 14)  , 15)
, 15) 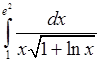 , 16)
, 16)  .
.
17)  , 18)
, 18) 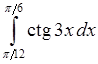 , 19)
, 19)  , 20)
, 20) 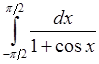 ,
,
21)  , 22)
, 22)  , 23)
, 23)  ,
,
24)  , 25)
, 25)  , 26)
, 26)  , 27)
, 27)  .
.
2. Обчислити визначений інтеграл за допомогою метода заміни змінної.
1) 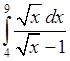 , 2)
, 2) 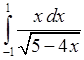 , 3)
, 3) 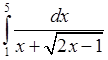 , 4)
, 4)  ,
,
5) 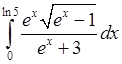 , 6)
, 6) 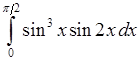 , 7)
, 7)  , 8)
, 8) 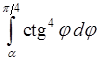 ,
,
9)  , 10)
, 10) 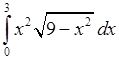 , 11)
, 11) 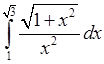 , 12)
, 12) 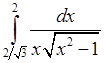 ,
,
13)  , 14)
, 14) 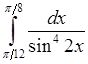 , 15)
, 15)  , 16)
, 16)  .
.
3. Обчислити визначений інтеграл методом інтегрування частинами.
1) 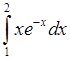 , 2)
, 2) 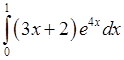 , 3)
, 3) 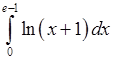 , 4)
, 4) 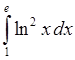 ,
,
5) 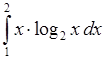 , 6)
, 6)  , 7)
, 7)  , 8)
, 8)  ,
,
9)  , 10)
, 10)  . 11)
. 11)  , 12)
, 12) 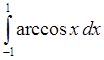 ,
,
13) 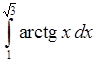 , 14)
, 14)  , 15)
, 15)  , 16)
, 16) 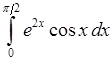 .
.
4. Обчислити невласний інтеграл I роду або встановити його розбіжність.
1) 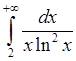 , 2)
, 2) 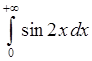 , 3)
, 3) 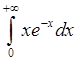 , 4)
, 4) 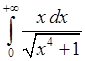 , 5)
, 5) 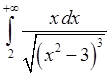 ,
,
6) 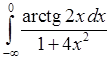 , 7)
, 7) 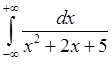 , 8)
, 8) 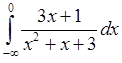 , 9)
, 9)  ,
,
10) 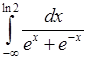 , 11)
, 11)  , 12)
, 12) 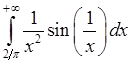 , 13)
, 13)  ,
,
14)  , 15)
, 15) 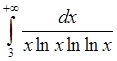 , 16)
, 16) 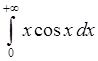 , 17)
, 17) 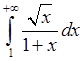 .
.
5. Обчислити невласний інтеграл II роду або встановити його розбіжність.
1)  , 2)
, 2)  , 3)
, 3) 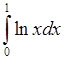 , 4)
, 4)  , 5)
, 5) 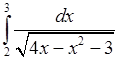 ,
,
6) 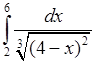 , 7)
, 7) 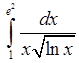 , 8)
, 8) 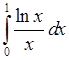 , 9)
, 9)  , 10)
, 10)  ,
,
11) 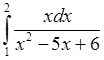 , 12)
, 12)  , 13)
, 13) 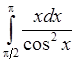 , 14)
, 14)  ,
,
15)  , 16)
, 16)  , 17)
, 17)  , 18)
, 18)  .
.
6. Дослідити на абсолютну та умовну збіжність невласний інтеграл.
1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  .
.
5)  , 6)
, 6) 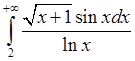 , 7)
, 7)  , 8)
, 8) 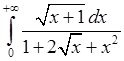 ,
,
9)  , 10)
, 10) 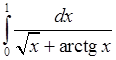 , 11)
, 11) 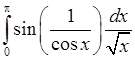 , 12)
, 12) 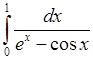 ,
,
13) 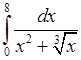 , 14)
, 14) 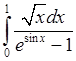 , 15)
, 15)  , 16)
, 16)  .
.
7. Обчислити площу фігури, обмеженої графіками функцій в прямокутній декартовій системі координат.
1) 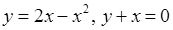 , 2)
, 2)  , 3)
, 3) 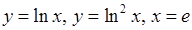 ,
,
4)  , 5)
, 5)  ,
,
6) 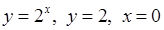 , 7)
, 7) 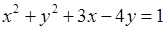 , 8)
, 8) 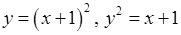 ,
,
9) 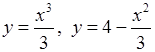 , 10)
, 10) 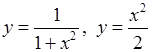 , 11)
, 11)  .
.
8. Обчислити площу фігури, обмеженої лініями, заданими рівняннями в параметричній формі.
1) 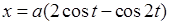 ,
,  ,
, 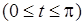 ,
,
2) 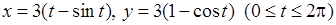 ,
,
3) 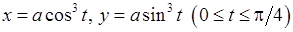 ,
,
4)  ,
,
5) 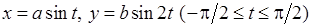 ,
,
6)  ,
,
7) 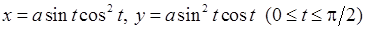 ,
,
8) 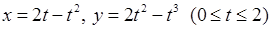 ,
,
9)  ,
,
10)  .
.
9. Обчислити площу фігури, обмеженої лініями, заданими рівняннями в полярній системі координат.
1) 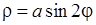 , 2)
, 2) 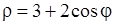 , 3)
, 3) 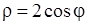 , 4)
, 4) 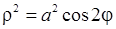 ,
,
5)  , 6)
, 6) 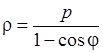 ,
,  ,
,
7) 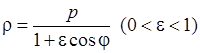 , 8)
, 8)  ,
, 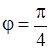 ,
,
9)  , 10)
, 10) 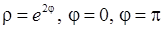 .
.
10. Обчислити довжину дуги кривої, заданої в прямокутній декартовій системі координат.
1)  , 2)
, 2)  , 3)
, 3) 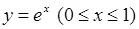 ,
,
4) 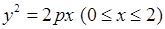 , 5)
, 5) 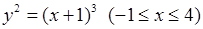 ,
,
6) 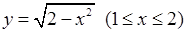 , 7)
, 7) 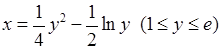 ,
,
8) 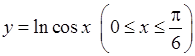 , 9)
, 9)  ,
,
10) 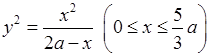 .
.
11. Обчислити довжину дуги кривої, заданої рівнянням в параметричній формі.
1) 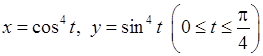 ,
,
2)  ,
,
3)  , 4)
, 4) 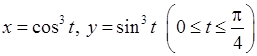 ,
,
5) 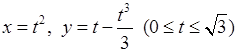 , 6)
, 6) 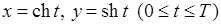 ,
,
7) 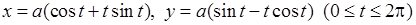 ,
,
8) 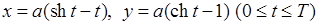 ,
,
9) 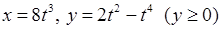 , 10)
, 10)  .
.
12. Обчислити довжину дуги кривої, заданої рівнянням в полярній системі координат.
1) 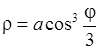 , 2)
, 2)  , 3)
, 3)  ,
,
4)  , 5)
, 5)  , 6)
, 6) 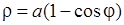 ,
,
7)  , 8)
, 8) 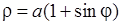 ,
,
9) 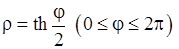 , 10)
, 10) 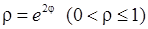 .
.
12. Знайти площу поверхні тіла, утвореного обертанням навколо осі 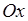 кри-
кри-
вої, заданої рівнянням в прямокутній декартовій системі координат.
1) 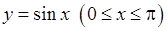 , 2)
, 2)  ,
,
3) 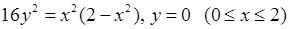 , 4)
, 4)  ,
,
5) 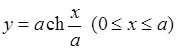 , 6)
, 6) 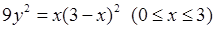 ,
,
7) 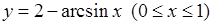 , 8)
, 8)  ,
,
9) 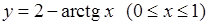 , 10)
, 10)  .
.
13. Знайти площу поверхні тіла, утвореного обертанням навколо осі 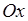 кривої, заданої рівнянням у параметричній формі.
кривої, заданої рівнянням у параметричній формі.
1) 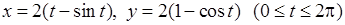 ,
,
2)  ,
,
3) 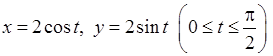 ,
,
4) 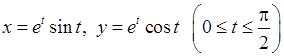 ,
,
5) 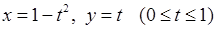 .
.
14. Знайти площу поверхні тіла, утвореного обертанням навколо полярної осі кривої, заданої рівнянням в полярній системі координат.
1) 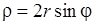 , 2)
, 2) 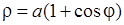 , 3)
, 3)  ,
,
4) 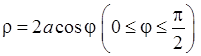 , 5)
, 5) 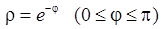 ,
,
6) 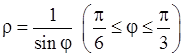 , 7)
, 7) 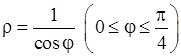 ,
,
8) 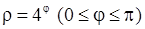 , 9)
, 9) 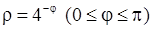 , 10)
, 10) 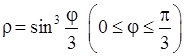 .
.
15. Знайти об’єм тіла, утвореного обертанням навколо вказаної осі фігури, обмеженої лініями, заданими рівняннями в прямокутній декартовій системі координат.
1) 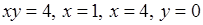 навколо осі
навколо осі 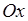 ,
,
2)  навколо осі
навколо осі 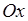 ,
,
3)  навколо осі
навколо осі 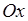 ,
,
4) 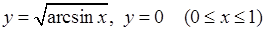 навколо осі
навколо осі 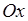 ,
,
5)  навколо осі
навколо осі 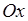 ,
,
6) 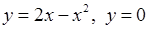 навколо осі
навколо осі  ,
,
7) 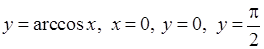 навколо осі
навколо осі  ,
,
8) 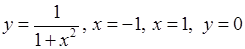 навколо осі
навколо осі  ,
,
9) 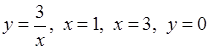 навколо осі
навколо осі  ,
,
10)  навколо осі
навколо осі  .
.
16. Знайти масу і координату центра ваги стрижня, розташованого на заданому відрізку осі 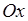 , якщо відома його лінійна густина
, якщо відома його лінійна густина  у кожній точці відрізку.
у кожній точці відрізку.
1)  ,
,  , 2)
, 2) 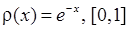 , 3)
, 3) 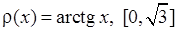 ,
,
4)  , 5)
, 5)  .
.
17. Знайти шлях, пройдений матеріальною точкою від моменту  до моменту
до моменту 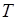 , якщо відома її миттєва швидкість
, якщо відома її миттєва швидкість  .
.
1) 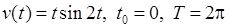 , 2)
, 2) 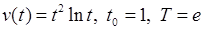 ,
,
3) 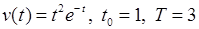 , 4)
, 4) 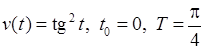 .
.
18. Знайти тиск рідини на вертикально занурену в неї платівку, якщо задано форму платівки.
1) півкруг, діаметр якого  і знаходиться на поверхні рідини;
і знаходиться на поверхні рідини;
2) рівнобічна трапеція, менша основа якої дорівнює  і лежить на поверхні рідини, більша основа дорівнює
і лежить на поверхні рідини, більша основа дорівнює 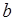 , висота
, висота 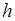 ;
;
3) рівнобічна трапеція, більша основа якої дорівнює 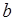 і лежить на поверхні рідини, менша основа дорівнює
і лежить на поверхні рідини, менша основа дорівнює  , висота
, висота 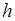 ;
;
4) рівнобедрений трикутник з основою  і бічними сторонами, довжина кожної з яких дорівнює
і бічними сторонами, довжина кожної з яких дорівнює  , причому вершина трикутника знаходиться на поверхні рідини, а основа паралельна поверхні;
, причому вершина трикутника знаходиться на поверхні рідини, а основа паралельна поверхні;
5) рівнобедрений трикутник з основою  і бічними сторонами, довжина кожної з яких дорівнює
і бічними сторонами, довжина кожної з яких дорівнює  , причому основа знаходиться на поверхні рідини.
, причому основа знаходиться на поверхні рідини.
19. Резервуар, який має форму циліндра, радіус основи якого 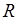 , а висота
, а висота 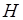 , цілком заповнений водою. Знайти час, на протязі якого вся вода витече з резервуару через круглий отвір у його дні, площа якого дорівнює
, цілком заповнений водою. Знайти час, на протязі якого вся вода витече з резервуару через круглий отвір у його дні, площа якого дорівнює 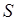 .
.
20. Резервуар, що має форму параболоїда обертання, утвореного обертанням параболи  навколо відрізка
навколо відрізка 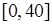 осі
осі 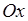 , цілком заповнений водою. Знайти час, за який вся вода витече з резервуару через круглий отвір у його дні, площа якого дорівнює 4 кв. од.
, цілком заповнений водою. Знайти час, за який вся вода витече з резервуару через круглий отвір у його дні, площа якого дорівнює 4 кв. од.
21. Обчислити інтеграл наближено за формулою Сімпсона, розбиваючи відрізок інтегрування на 10 рівних частин. Оцінити похибку. Порівняти знайдене наближене значення з його точним значенням.
1)  , 2)
, 2) 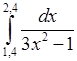 , 3)
, 3) 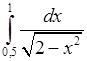 , 4)
, 4) 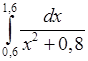 .
.
[1] Діріхле Петер Густав Лежен (1805–1859) – німецький математик.
[2] Дарбу Жан Гастон (1842–1917) – французький математик.
* Ньютон Ісаак (1643–1727) – видатний англійський математик і фізик.
Лейбніц Готфрід Вільгельм (1646–1716) – німецький математик, філософ і дипломат.
* Пуассон Сімеон Дені (1781–1840) – французький математик, механік і фізик.
[3] Паскаль Блез (1623–1662) – французький математик, фізик і філософ, один з творців інтегрального зчислення, а також теорії ймовірностей.
[4] Торрічеллі Еванджеліста (1608–1647) – італійський фізик та математик.
[5] Сімпсон Томас (1710–1761) – англійський математик.
Дата добавления: 2015-10-30; просмотров: 287 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Фізичні застосування визначеного інтеграла. | | | Глава вторая. ЕВРОПЕЙСКИЕ ИСТОКИ МЕНЕСТРЕЛЕЙ 1 страница |