Заміна змінної та інтегрування за частинами у визначеному інтегралі.

Як і у випадку невизначеного інтеграла, у визначеному інтегралі також можна застосовувати формули заміни змінної та інтегрування за частинами. Але тут вони мають певні особливості, до розглядання яких ми зараз й перейдемо.

Теорема. Нехай функція неперервна на відрізку , а функція 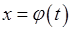задовольняє наступні умови:

1) 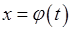визначена і неперервна на деякому проміжку 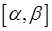і відображає проміжок 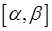на проміжок ,

2) ,

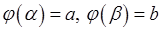3) 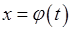неперервно диференційовна на .

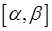Тоді справедлива формула заміни змінної:

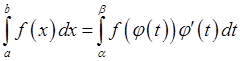. (7.1)

Доведення. Маємо:

, де 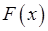– первісна функції на відрізку . Легко переконатися у тому, що функція 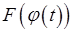є первісною для функції 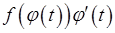на відрізку 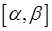. Дійсно, оскільки , то за формулою для похідної складеної функції матимемо:

.

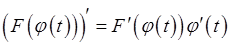Отже можемо записати:

.

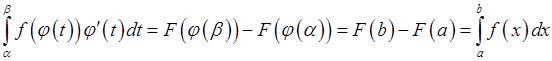Теорему доведено.

Розглянемо приклади використання цієї теореми.

1. Обчислити інтеграл

.

Зробимо заміну змінної 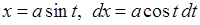, де .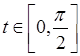

Відповідність інтервалів відносно і відносно 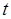зручно зображувати за допомогою таблички:

 

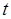
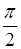
Отже матимемо:

.

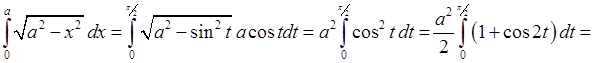
2. У багатьох випадках підстановку зручніше брати не у вигляді залежності від 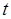(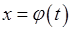), а у вигляді залежності 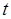від (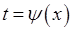). Розглянемо інтеграл:

.

Використаємо заміну 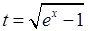. Тоді , ,

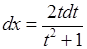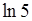
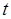
Отже

.

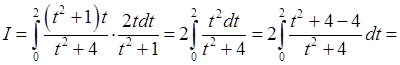
Зауважимо, що на відміну від метода заміни змінної у невизначеному

інтегралі, тут нема необхідності повертатися до старої змінної, оскільки межі інтегрування змінюються водночас зі змінною інтегрування. Нові межі підставляються до нової змінної.

Встановимо за допомогою заміни змінної наступні корисні тверджен-

ня:

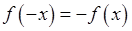1). Якщо функція є непарною, тобто , то 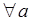виконано:

.

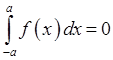Тобто інтеграл в симетричних межах від непарної функції дорівнює нулю. Дійсно, розіб’ємо цей інтеграл на два:

.

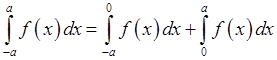У першому інтегралі зробимо підстановку 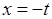, тоді ,

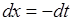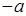
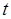
Матимемо:

.

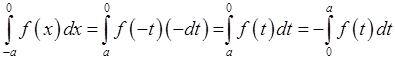І тому

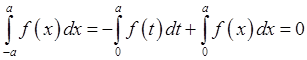, що й треба було довести.

Наприклад без обчислень можна одразу стверджувати рівності:

,

.

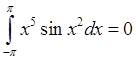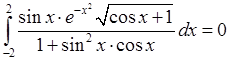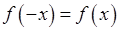2). Якщо функція парна, тобто , то :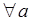

.

Це твердження доводиться аналогічно попередньому, зробіть це самостійно.

3). Якщо функція періодична з періодом , тобто , то :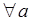

.

Тобто інтеграли по будь якому проміжку, довжина якого дорівнює періоду функції, співпадають. Дійсно, розіб’ємо інтеграл на три інтеграли:

. (7.2)

У останньому з цих інтегралів зробимо заміну 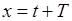, тоді ,

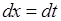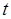
Матимемо:

.

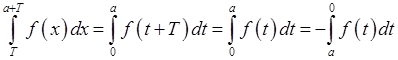Таким чином третій інтеграл у формулі (7.2) дорівнює першому з протилежним знаком. Звідси й випливає потрібне твердження.

Для визначеного інтеграла має місце формула інтегрування за частинами:

. (7.3)

Всі рекомендації щодо вибору функцій 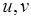, які були сформульовані для невизначеного інтеграла, зберігаються і для визначеного. Розглянемо приклади.

1.

.

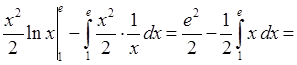
2.

.

Дата добавления: 2015-10-30