
Читайте также:
|
Оскільки ми побачили, що дві різні задачі приводять до однієї математичної моделі, ми тепер не будемо прив’язуватись до конкретної задачі з навколишньої дійсності, а розглянемо проблему в абстрактному сенсі. Отже нехай ми маємо деяку функцію  , яка визначена на відрізку
, яка визначена на відрізку  . Розіб’ємо цей відрізок на
. Розіб’ємо цей відрізок на 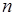 частин довільно обраними точками ділення:
частин довільно обраними точками ділення:
 .
.
На кожному з частинних відрізків 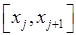
 довільним чином оберемо точку
довільним чином оберемо точку 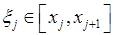 і побудуємо суму:
і побудуємо суму:
 , (2.1) де
, (2.1) де  – довжина відрізка
– довжина відрізка 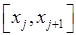 . Сума (2.1) називається інтегральною сумою функції
. Сума (2.1) називається інтегральною сумою функції  , яка відповідає даному розбиттю відрізка
, яка відповідає даному розбиттю відрізка  на частинні та даному вибору проміжних точок
на частинні та даному вибору проміжних точок  .
.
Легко помітити, що з геометричної точки зору інтегральна сума у випадку, коли  , дорівнює площі ступінчатої фігури (рис. 3).
, дорівнює площі ступінчатої фігури (рис. 3).
Позначимо  і назвемо цю величину рангом розбиття. Це буде означати, що жоден з частинних відрізків за довжиною не перевищує величини
і назвемо цю величину рангом розбиття. Це буде означати, що жоден з частинних відрізків за довжиною не перевищує величини  .
.
Означення. Якщо існує скінченна границя інтегральної суми (2.1) при  , яка не залежить від засобу розбиття відрізка
, яка не залежить від засобу розбиття відрізка  на частинні і не залежить від засобу обрання проміжних точок
на частинні і не залежить від засобу обрання проміжних точок  , то ця границя називається визначеним інтегралом функції
, то ця границя називається визначеним інтегралом функції  на відрізку
на відрізку  і позначається символом:
і позначається символом:
 .
.
Тобто:
 . (2.2)
. (2.2)
Символ  був введений Г.Лейбніцем у 1686 році. Цей символ є дещо деформованою буквою
був введений Г.Лейбніцем у 1686 році. Цей символ є дещо деформованою буквою 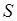 (перша буква слова Summa). Термін «інтеграл» (від латинського integer – цілий) був запропонований у 1696 році Іоганом Бернулі. Наведене означення інтеграла належить Бернгарду Ріману (1826–1866), він же сформулював умови його існування. Тому таким чином введений інтеграл називається інтегралом Рімана.
(перша буква слова Summa). Термін «інтеграл» (від латинського integer – цілий) був запропонований у 1696 році Іоганом Бернулі. Наведене означення інтеграла належить Бернгарду Ріману (1826–1866), він же сформулював умови його існування. Тому таким чином введений інтеграл називається інтегралом Рімана.
Якщо границя (2.2) існує, то функція  називається інтегровною на відрізку
називається інтегровною на відрізку  . Числа
. Числа  і
і  називаються відповідно нижньою та верхнею межею інтегрування. Функція
називаються відповідно нижньою та верхнею межею інтегрування. Функція  називається підінтегральною функцією, а вираз
називається підінтегральною функцією, а вираз  називається підінтегральним виразом. Змінна
називається підінтегральним виразом. Змінна  називається змінною інтегрування, а проміжок
називається змінною інтегрування, а проміжок  – проміжком інтегрування.
– проміжком інтегрування.
Повертаючись до розглянутих у п. 1 задач, тепер можна сказати, що
1) площа 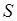 криволінійної трапеції, обмеженої прямими
криволінійної трапеції, обмеженої прямими  і графіком функції
і графіком функції  , дорівнює визначеному інтегралу від цієї функції на відрізку
, дорівнює визначеному інтегралу від цієї функції на відрізку  :
:
 .
.
У цьому полягає геометричний зміст інтеграла.
2) робота  змінної сили
змінної сили  , що діє вздовж відрізка
, що діє вздовж відрізка  , дорівнює визначеному інтегралу від сили:
, дорівнює визначеному інтегралу від сили:
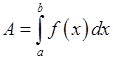 .
.
У цьому полягає фізичний зміст інтеграла.
Виникає питання, які умови повинна задовольняти інтегровна на відрізку  функція
функція  ? Відповідь на це питання дають наступні теореми.
? Відповідь на це питання дають наступні теореми.
Теорема 1 (необхідна умова інтегровності). Якщо функція  інтегровна на відрізку
інтегровна на відрізку  , то вона обмежена на цьому відрізку.
, то вона обмежена на цьому відрізку.
Доведення. Припустимо протилежне, тобто, що функція  необмежена на відрізку
необмежена на відрізку  . Тоді для будь якого розбиття відрізка
. Тоді для будь якого розбиття відрізка  на частинні функція
на частинні функція  буде необмеженою хоча б на одному з них. Без обмеження загальності вважатимемо, що функція необмежена на відрізку
буде необмеженою хоча б на одному з них. Без обмеження загальності вважатимемо, що функція необмежена на відрізку  . Обравши на решті відрізків точки
. Обравши на решті відрізків точки  довільним чином, позначимо:
довільним чином, позначимо:
 .
.
Візьмемо тепер довільне 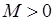 і оберемо точку
і оберемо точку  на відрізку
на відрізку  так, щоб було виконано:
так, щоб було виконано:
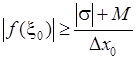 , що завжди можна зробити внаслідок необмеженості функції
, що завжди можна зробити внаслідок необмеженості функції  на відрізку
на відрізку  . Тоді
. Тоді
 .
.
Складемо інтегральну суму:
 .
.
Матимемо:
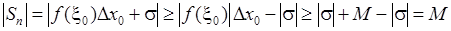 , тобто інтегральну суму за рахунок вибору точки
, тобто інтегральну суму за рахунок вибору точки  можна за абсолютною величиною зробити більше, ніж будь яке наперед задане число. Тому у інтегральної суми не існує скінченної границі при
можна за абсолютною величиною зробити більше, ніж будь яке наперед задане число. Тому у інтегральної суми не існує скінченної границі при  , а тоді функція
, а тоді функція  не є інтегровною на відрізку
не є інтегровною на відрізку  всупереч умові теореми. Теорему доведено.
всупереч умові теореми. Теорему доведено.
Зауваження. Обернене твердження до цієї теореми несправедливе, тобто з обмеженості функції на відрізку не випливає її інтегровність на цьому відрізку. Класичним прикладом такої функції є так звана функція Діріхле[1].

Ця функція на відрізку  обмежена, оскільки
обмежена, оскільки  . Доведемо, що вона не інтегровна на відрізку
. Доведемо, що вона не інтегровна на відрізку  . Розіб’ємо відрізок
. Розіб’ємо відрізок  довільним чином на частинні відрізки і складемо інтегральну суму
довільним чином на частинні відрізки і складемо інтегральну суму
 .
.
Якщо обрати точки 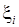 раціональними, то
раціональними, то  і тоді
і тоді
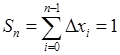 ,
,  .
.
Якщо обрати точки 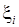 ірраціональними, то
ірраціональними, то 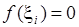 і тоді
і тоді
 ,
,  .
.
Таким чином границя інтегральної суми залежить від вибору точок 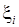 , а це означає, що функція
, а це означає, що функція  не є інтегровною на
не є інтегровною на  .
.
Отже обмеженість функції на відрізку є необхідною умовою інтегровності, але не є достатньою. Наступна теорема, яку ми наводимо без доведення, дає достатню умову інтегровності.
Теорема 2 (достатня умова інтегровності). Якщо функція неперервна на відрізку  , то вона інтегровна на цьому відрізку.
, то вона інтегровна на цьому відрізку.
Обернене твердження до цієї теореми також несправедливе – інтегровними можуть бути і деякі розривні функції. Тобто теорема 2 тільки достатня умова інтегровності, але не необхідна.
Разом з цим існує критерій (тобто необхідна і достатня умова) інтегровності функції на відрізку. Для цього введемо наступні поняття. Розіб’ємо відрізок  на частинні довільно обраними точками ділення:
на частинні довільно обраними точками ділення:
 .
.
Позначимо:  ,
,  . Складемо суми:
. Складемо суми:
 ,
,  .
.
Ці суми називаються відповідно нижньою та верхньою сумами Дарбу [2]. Зокрема, якщо функція  неперервна на відрізку
неперервна на відрізку  (отже, й на кожному з частинних відрізків), суми Дарбу є найменшою та найбільшою з інтегральних сум, що відповідають даному розбиттю. Справді, у цьому випадку функція
(отже, й на кожному з частинних відрізків), суми Дарбу є найменшою та найбільшою з інтегральних сум, що відповідають даному розбиттю. Справді, у цьому випадку функція  досягає на кожному з частинних відрізків свого найбільшого та найменшого значень, отже точку
досягає на кожному з частинних відрізків свого найбільшого та найменшого значень, отже точку 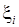 на відрізку
на відрізку 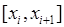 можна обрати так, щоб, за бажанням, було
можна обрати так, щоб, за бажанням, було  , або
, або  . У загальному випадку:
. У загальному випадку:
 .
.
Домножаючи всі частини цієї нерівності на  та, підсумовуючи за індексом
та, підсумовуючи за індексом  , матимемо:
, матимемо:
 , де
, де  – інтегральна сума (2.1). При фіксованому розбитті суми
– інтегральна сума (2.1). При фіксованому розбитті суми  та
та 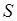 будуть сталими числами, що не залежать від точок
будуть сталими числами, що не залежать від точок 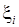 , в той час, як сума
, в той час, як сума  від цих точок залежить. Але за рахунок обрання точок
від цих точок залежить. Але за рахунок обрання точок 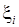 значення
значення  можна зробити як завгодно близьким як до
можна зробити як завгодно близьким як до  , так й до
, так й до  , отже суму
, отже суму  можна зробити як завгодно близькою як до
можна зробити як завгодно близькою як до  , так й до
, так й до 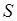 . А тоді для даного розбиття суми
. А тоді для даного розбиття суми  та
та 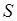 є точними нижньою та верхньою межами для інтегральних сум.
є точними нижньою та верхньою межами для інтегральних сум.
Суми Дарбу мають наступні властивості:
Властивість 1. Якщо до тих точок ділення, що є, додати нові точки, то нижня сума Дарбу може лише збільшитися, а нижня – лише зменшитися.
Доведення. Можна обмежитися додаванням лише однієї точки ділення  . Нехай ця точка потрапить між точками
. Нехай ця точка потрапить між точками  та
та  , тобто
, тобто  . Нехай
. Нехай  – нова верхня сума Дарбу, яка отримується внаслідок такого додавання. Вона буде відрізнятися від суми
– нова верхня сума Дарбу, яка отримується внаслідок такого додавання. Вона буде відрізнятися від суми 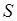 тим, що в сумі
тим, що в сумі 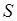 проміжку
проміжку  відповідав доданок
відповідав доданок  , а в сумі
, а в сумі  цьому проміжку відповідає сума двох доданків:
цьому проміжку відповідає сума двох доданків:
 , де
, де  ,
,  – точні верхні межі функції
– точні верхні межі функції  у проміжках
у проміжках  та
та  . Оскільки ці проміжки є частинами проміжку
. Оскільки ці проміжки є частинами проміжку  , то
, то  ,
,  , отже
, отже
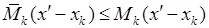 ,
, 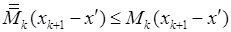 .
.
Отже

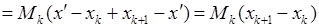 , звідки випливає, що
, звідки випливає, що  . Аналогічно доводиться і нерівність для нижньої суми Дарбу.
. Аналогічно доводиться і нерівність для нижньої суми Дарбу.
Властивість 2. Кожна нижня сума Дарбу не більше кожної верхньої суми, навіть якщо ця верхня сума відповідає іншому розбиттю.
Доведення. Розіб’ємо відрізок  довільним чином на частинні відрізки і складемо для цього розбиття суми Дарбу
довільним чином на частинні відрізки і складемо для цього розбиття суми Дарбу  та
та  . Розглянемо тепер інше розбиття відрізку
. Розглянемо тепер інше розбиття відрізку  і для нього також складемо відповідні суми Дарбу
і для нього також складемо відповідні суми Дарбу  та
та  .
.
Покажемо, що  . Об’єднаємо обидва розбиття, тоді отримаємо третє розбиття, якому відповідатимуть суми
. Об’єднаємо обидва розбиття, тоді отримаємо третє розбиття, якому відповідатимуть суми  та
та  . На підставі Властивості 1 маємо:
. На підставі Властивості 1 маємо:  та
та  . Але оскільки
. Але оскільки  , то
, то  , що й треба було довести.
, що й треба було довести.
З доведеного випливає, що вся множина  нижніх сум Дарбу обмежена зверху, наприклад, будь якою верхньою сумою. Тому множина
нижніх сум Дарбу обмежена зверху, наприклад, будь якою верхньою сумою. Тому множина  має точну верхню межу
має точну верхню межу
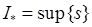 , і, крім того,
, і, крім того,  для будь якої верхньої суми
для будь якої верхньої суми 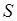 . Тоді множина
. Тоді множина  верхніх сум обмежена знизу, отже існує
верхніх сум обмежена знизу, отже існує
 , причому
, причому  . Таким чином, для будь якої нижньої
. Таким чином, для будь якої нижньої  та для будь якої верхньої
та для будь якої верхньої 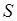 суми Дарбу маємо:
суми Дарбу маємо:
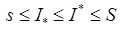 . (2.3)
. (2.3)
Числа  та
та  називають відповідно нижнім та верхнім інтегралом Дарбу.
називають відповідно нижнім та верхнім інтегралом Дарбу.
Теорема 3. (необхідна і достатня умова інтегровності функції). Для інтегровності функції  на відрізку
на відрізку  необхідно і достатньо, щоб
необхідно і достатньо, щоб
 . (2.4)
. (2.4)
Доведення. Необхідність. Нехай функція  інтегровна на
інтегровна на  , тобто існує
, тобто існує
 , де
, де  – інтегральна сума (2.1). Ц означає, що для будь якого
– інтегральна сума (2.1). Ц означає, що для будь якого  знайдеться таке
знайдеться таке  , що, як тільки
, що, як тільки  , то буде виконано:
, то буде виконано:
 для будь якого вибору точок
для будь якого вибору точок 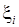 . Або:
. Або:
 .
.
Але суми Дарбу  та
та 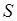 є точними нижньою та верхньою межами для
є точними нижньою та верхньою межами для  , тому:
, тому:
 , отже
, отже
 , звідки й випливає рівність (2.4).
, звідки й випливає рівність (2.4).
Достатність. Нехай виконано умову (2.4). Тоді з (2.3) випливає, що  , і якщо позначити
, і якщо позначити  , то
, то
 .
.
Нехай інтегральна сума  відповідає тому ж розбиттю, що й суми
відповідає тому ж розбиттю, що й суми  та
та 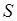 . Тоді
. Тоді
 .
.
Згідно з (2.4) для будь якого  існує таке
існує таке  , що, як тільки
, що, як тільки  , то виконується
, то виконується  . Але тоді і
. Але тоді і  , оскільки
, оскільки  та
та  знаходяться між
знаходяться між  та
та 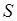 . А це означає, що
. А це означає, що
 , тобто функція
, тобто функція  інтегровна на
інтегровна на  .
.
Теорему доведено.
Дата добавления: 2015-10-30; просмотров: 1067 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачі, що приводять до поняття визначеного інтеграла. | | | Властивості визначеного інтеграла. |