Розв`язання прикладів

Приклад 1. Обчислити невласний інтеграл .

Розв`язання. За означенням,

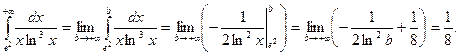
Отже, даний інтеграл збігається.

Приклад 2. Обчислити невласний інтеграл .

Розв`язання. За означенням,

Таким чином, даний інтеграл збігається.

Приклад 3. Обчислити невласний інтеграл .

Розв`язання. За означенням,

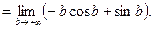
Оскільки остання границя не існує, то невласний інтеграл розбігається.

Приклад 4. Обчислити інтеграл

Розв`язання. Покладемо Тоді i

Одержали невласний інтеграл. Обчислюючи його за означенням, будемо мати

Таким чином, заданий інтеграл

Приклад 5. Обчислити невласний інтеграл або установити його розбіжність.

Розв`язання. За означенням,

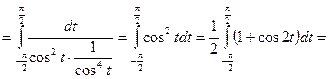
Отже, даний інтеграл збігається.

Тут слід зауважити, що після заміни змінної у невласному інтегралі, одержали визначений інтеграл.

Приклад 6. Дослідити на збіжність невласний інтеграл

Розв`язання. Підінтегральна функція на проміжку

(a= 1>0 ) i при

В силу ознаки 5 збіжності невласних інтегралів, вихідний інтеграл

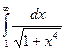збігається, бо i c= 1 (c=const),

Іншими словами із збіжності більшого невласного інтеграла випливає збіжність меншого невласного інтеграла

Приклад 7. Дослідити на збіжність інтеграл де

Розв`язання. Оскільки 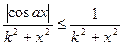i

збігається, то за ознакою 1 інтеграл збігається. Тоді збігається, і до того ж абсолютно, і заданий інтеграл

Приклад 8. Довести збіжність інтеграла

Розв`язання. Відкидаючи менші члени чисельника і знаменника, бачимо, що даний інтеграл збігається або розбігається одночасно з інтегралом

бо

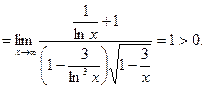
Невласний інтеграл

збігається, отже, збігається і заданий інтеграл.

Приклад 9. Довести, що збігається.

Розв`язання. Очевидно, що Звідси або і тому або . Оскільки

збігається, то на основі ознаки 3 збігається і інтеграл

А так як то на основі ознаки 1, збігається і інтеграл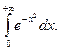

Замінюючи в цьому інтегралі х на – у, приходимо до висновку, що збігається і (назва змінної інтегрування не змінює величину визначеного інтеграла). Із збіжності інтегралів і випливає збіжність

Відзначимо, що має важливе значення в теорії ймовірностей. Як уже відзначалося раніше, через елементарні функції не виражається.

Приклад 10. Дослідити на збіжність інтеграл 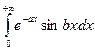і обчислити його (а > 0).

Розв`язання. Так як при а > 0 збігається (пропонуємо читачеві довести збіжність цього інтеграла самостійно), а то на основі ознаки 1 збігається і інтеграл Тоді на основі ознаки 4

збігається і заданий інтеграл.

Застосовуючи двічі формулу інтегрування частинами, легко показати (це ми також пропонуємо читачеві зробити самостійно), що для функції 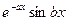первісна функція

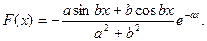
Тому

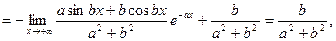
оскільки під знаком границі чисельник дробу – величина обмежена, а

при а > 0. Отже, даний невласний інтеграл 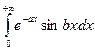збігається до числа

Вправи

Обчислити невласні інтеграли або установити їх розбіжність:

1. Відповідь: 1–ln2.

2. Відповідь: розбігається.

3. 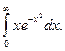Відповідь: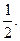

4. Відповідь: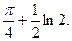

5. 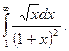Відповідь:

6. Відповідь: 2.

7. Відповідь: розбігається.

8. Відповідь: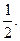

9. Відповідь: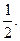

10. Відповідь:

Дослідити на збіжність інтеграли:

11. Відповідь: розбігається.

12. Відповідь: збігається.

13. Відповідь: розбігається.

14. Відповідь: розбігається.

15. Відповідь: розбігається.

2.10. Невласні інтеграли від необмежених функцій

Якщо функція f(x) не обмежена в будь-якому околі точки c відрізка і неперервна при і то за означенням

(37)

де і змінюються незалежно одне від одного. У випадку с=в або с=а

(38)

або

(39)

Якщо границі, які стоять у правих частинах рівностей (37), (38), (39), існують і скінченні, то невласний інтеграл називають збіжним.

Якщо ж ці границі не існують або дорівнюють нескінченності, то невласний інтеграл називають розбіжним.

Підкреслимо, що невласний інтеграл виражений рівністю (37), називають збіжним лише в тому випадку, коли обидві границі правої частини існують і скінченні.

Якщо ж принаймні одна з цих границь не існує або дорівнює нескінченності, то невласний інтеграл називають розбіжним.

Зауважимо, що позначення невласного інтеграла від необмеженої функції за формою не відрізняється нічим від позначення визначеного інтеграла. Тому, щоб розрізнити, буде інтеграл визначеним чи невласним, треба перевірити, буде чи ні функція f (x) інтегровною на відрізку .

Якщо функція f (x)необмежена на проміжку або на проміжку або в будь-якому околі точки c відрізка то інтеграл буде невласним.

Відзначимо також, що коли функція f (x) необмежена в будь-якому околі точки c відрізка й існує неперервна на функція F (x) така, що

при то

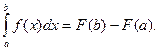(40)

2.11. Ознаки збіжності невласних інтегралів від необмежених функцій

1. Якщо f (x) і – дві невід`ємні необмежені функції на піввідрізку інтегровні на кожному відрізку де і якщо

для

де с –константа, то із збіжності невласного інтеграла випливає збіжність невласного інтеграла 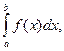а з розбіжності невласного інтеграла випливає розбіжність невласного інтеграла .

2. Нехай f (x) невід`ємна і необмежена на піввідрізку і інтегровна на кожному відрізку , де .

Якщо існують такі числа , M> 0 і , що

для ,

то невласний інтеграл збігається.

Якщо існують такі числа , M> 0 i , що

для ,

то невласний інтеграл розбігається.

3. Нехай f (x) визначена на проміжку , необмежена на цьому проміжку і інтегровна на кожному відрізку , де .

Якщо збігається невласний інтеграл , то збігається і невласний інтеграл . Відзначимо, що в цьому випадку невласний інтеграл називають абсолютно збіжним. Якщо ж невласний інтеграл збігається, а невласний інтеграл розбігається, то невласний інтеграл називають умовно збіжним.

Як бачимо, ознаки збіжності невласних інтегралів від необмежених функцій багато в чому аналогічні відповідним ознакам збіжності невласних інтегралів з нескінченними проміжками інтегрування.

Дата добавления: 2015-10-30