
|
Читайте также: |
Приклад 1. Знайти 
Розв`язання. Підінтегральна функція є раціональною функцією від дробових степенів х. Отже, маємо інтеграл першого типу від ірраціональної функції. Тут n 1=2, n 2=3, n 3=4, тому к= 12 (найменше спільне кратне чисел 2, 3 і 4). Покладемо x=t 12. Тоді

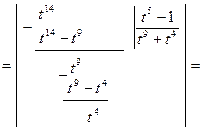
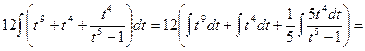
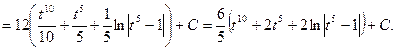
Повертаючись до змінної х, остаточно будемо мати
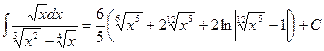 .
.
Приклад 2. Знайти 
Розв`язання. Маємо інтеграл другого типу від ірраціональної функції. Тут n 1=3, n 2=2, тому к= 6. Використовуючи підстановку 2 x+ 1 =t 6, звідки 
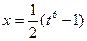 i dx= 3 t 5 dt, одержимо
i dx= 3 t 5 dt, одержимо
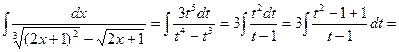
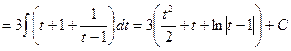 .
.
Оскільки  то повертаючись до змінної х, будемо мати
то повертаючись до змінної х, будемо мати
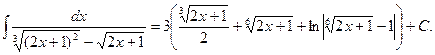
Приклад 3. Знайти 
Розв`язання. Виділимо з квадратного тричлена повний квадрат:
9 х2- 6 х+ 2=9 х 2-6 х +1+1=(3 х -1)2+1.
Тоді, враховуючи також, що d (3 x -1)=3 dx, одержимо табличний інтеграл (20):
 .
.
Приклад 4. Знайти 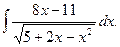
Розв`язання. Спочатку в чисельнику виділимо похідну підкореневого виразу, після чого розкладемо інтеграл на суму двох інтегралів. Тоді
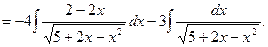
Перший з одержаних інтегралів є табличний інтеграл (4), а другий зведеться до табличного інтеграла (19) шляхом виділення повного квадрата з квадратного тричлена 5+2 х-х 2.
Виділяючи повний квадрат, будемо мати
5+2 х-х 2=-(х 2-2 х -5)=-(х 2-2 х +1-6)=6-(х -1)2.
Отже,
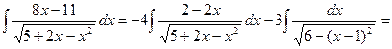
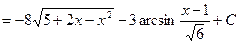 .
.
Приклад 5. Знайти 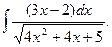
Розв`язання. Як і в попередньому прикладі маємо
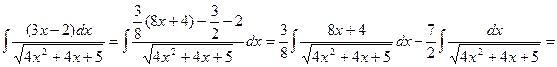

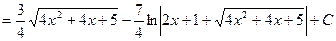 .
.
Зауважимо, що розв`язати аналогічні приклади можна й іншим способом. Покажемо це на прикладі 5.
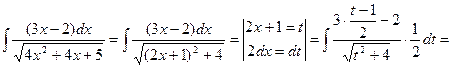
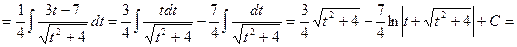
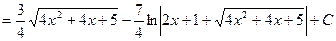 .
.
Приклад 6. Знайти 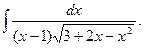
Розв`язання. Покладемо  тоді
тоді 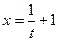 i
i 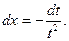 Отже,
Отже,
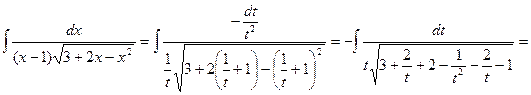

 .
.
ВПРАВИ
Знайти інтеграли:
1. 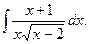 Відповідь:
Відповідь: 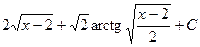 .
.
2.  Відповідь:
Відповідь: 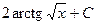 .
.
3.  Відповідь:
Відповідь: 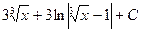 .
.
4.  Відповідь:
Відповідь:  .
.
5. 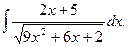 Відповідь:
Відповідь: 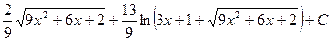 .
.
6. 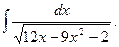 Відповідь:
Відповідь: 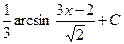 .
.
7.  Відповідь:
Відповідь: 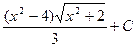 .
.
8. 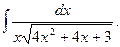 Відповідь:
Відповідь:  .
.
9.  Відповідь:
Відповідь:  .
.
10.  Відповідь:
Відповідь:  .
.
Інтегрування тригонометричних функцій
Інтеграли від тригонометричних функцій, як і від функцій ірраціональних, не завжди можна знайти.Однак можна вказати на підклас таких функцій, інтеграли від яких виражаються в скінченному вигляді. В цей підклас тригонометричних функцій входять тригонометричні функції, що є раціональними функціями від sin x, cos x, tg x, ctg x, sec x, cosec x. Оскільки tg x, ctg x, sec x, cosec x самі виражаються раціонально через sin x i cos x, то цей підклас можна охарактеризувати як підклас тригонометричних функцій, які є раціональними функціями від sin x i cos x.
І. Інтеграл вигляду 
де R –раціональна функція від sin x i cos x за допомогою так званої універсальної тригонометричної підстановки
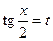
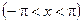
зводиться до інтегралу від раціональної функції. При цьому
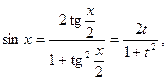
 ,
,
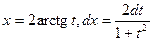 .
.
Зауважимо, що іноді замість підстановки 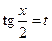 вигідніше зробити підстановку
вигідніше зробити підстановку 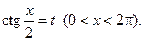
Слід також відзначити, що в силу своєї універсальності підстановка 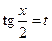 часто веде до занадто громіздких викладок, що ускладнює знаходження інтеграла. Тому в окремих випадках доцільно застосовувати інші підстановки, які також раціоналізують інтеграл.
часто веде до занадто громіздких викладок, що ускладнює знаходження інтеграла. Тому в окремих випадках доцільно застосовувати інші підстановки, які також раціоналізують інтеграл.
Нижче укажемо випадки, коли мета буде досягнута за допомогою більш простих підстановок.
ІІ. Інтеграл вигляду 
де R – раціональна функція від sin x і cos x.
а) Якщо виконується рівність
R (- sin x, cos x)  - R (sin x, cos x),
- R (sin x, cos x),
то вигідно застосувати підстановку cos x=t.
б) Якщо виконується рівність
R (sin x, -cos x)  - R (sin x, cos x)
- R (sin x, cos x)
то доцільно застосувати підстановку sin x=t.
в) Якщо виконується рівність
R (-sin x, -cos x)  R (sin x, cos x)
R (sin x, cos x)
то застосовують підстановку tg x=t або ctg x=t, при цьому, якщо tg x=t, то
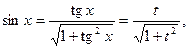

 .
.
Зокрема,
1.  підстановкою sin x=t зводиться до
підстановкою sin x=t зводиться до 
2.  підстановкою cos x=t зводиться до
підстановкою cos x=t зводиться до 
3.  підстановкою tg x=t зводиться до
підстановкою tg x=t зводиться до 
ІІІ. Інтеграл вигляду  .
.
а) Якщо m i n –цілі числа і принаймні одне із цих чисел непарне додатне число, наприклад m= 2 k+1,
тоді


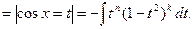
Якщо ж непарним буде число n= 2 p+ 1>0, то треба застосувати підстановку t= sin x. Тоді


б) Якщо обидва показники m i n –парні невід`ємні числа(зокрема, один із них може бути рівним нулю), то доцільно застосувати формули
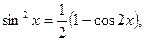
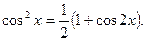
 в) Якщо обидва показники – парні, причому принаймні один із них від`ємний, то треба зробити заміну tg x=t або ctg x=t.
в) Якщо обидва показники – парні, причому принаймні один із них від`ємний, то треба зробити заміну tg x=t або ctg x=t.
Зауважимо, що інтеграли вигляду  дуже зручно знаходити за допомогою рекурентних формул.
дуже зручно знаходити за допомогою рекурентних формул.

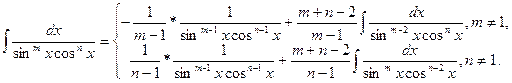
IV. Інтеграл вигляду  або
або 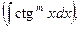
де m - ціле додатне число. Для знаходження такого інтеграла застосовують формулу
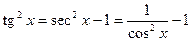 (або
(або 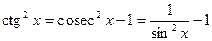 ),
),
за допомогою якої послідовно знижується степінь тангенса або котангенса.
V. Інтеграли вигляду
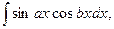
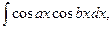
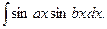
Щоб знайти ці інтеграли, треба перейти від добутку тригонометричних функцій до суми за відомими формулами:
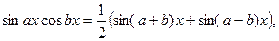
 (28)
(28)
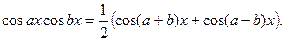
VI. Інтеграли вигляду 
Такі інтеграли беруть за допомогою універсальної підстановки 
VII. Інтеграли вигляду 
Для знаходження цих інтегралів доцільно застосувати підстановку t= tg x.
Дата добавления: 2015-10-30; просмотров: 300 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Інтегрування ірраціональних функцій | | | Розв`язання прикладів |