Уравнения движения

Разомкнутые импульсные системы. Эти системы в общем случае могут быть представлены последовательным соединением ИЭ и НЧ (см. рисунок 14.1). анализ таких систем целесообразнее всего производить в относительном

времени

t = t / T = n,

используя дискретное преобразование Лапласа и сохраняя

при этом те же удобства, которые имеет обычное преобразование Лапласа при решении дифференциальных уравнений.

Представим импульсный элемент ИЭ и виде поледовательного соедине- ния простейщего

x(t) ИЭ

y(t)

НЧ z(t)

x(t) y(t) z(t)

t t t

Рисунок 14.1. Структурная схема разомкнутой импульсной системы: ИЭ – импульсный элемент; НЧ – непрерывная часть

T t

A АИМ

t

уT

ШИМ

ЕT ВИМ

Рисунок 14.2. Виды импульсной модуляции

x(t) ИЭ

ПИЭ ФЭ

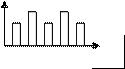y1(t) y(t)

t t

Рисунок 14.3. Структурная схема импульсного элемента

ПНЧ

Wф(q) WH(q)

x(t)

ПИЭ

y1(t)

y(t)

ФЭ

НЧ

W(q)

z(t)

ИЭ

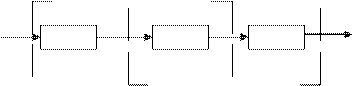
Рисунок 14.4. Преобразованная структурная схема разомкнутой импульс-

ной системы

импульсного элемента ПИЭ и формирующего элемента ФЭ (рисунок 14.3). В

простейшем импульсном элементы непрерывная функция

x (t) преобразуется в

решетчатую

y 1(t) или в относительном времени

t = n

x n ]

преобразуется в

y 1 n ].

Формирующий элемент ФЭ из ординат решетчатой функции

y n ]

формирует

импульсы определенной формы в зависимости от типа импульсной модуляции; ФЭ для линейных импульсных элементов в динамическом отношении может

быть представлен передаточной функцией

Wфp ]

или для относительного вре-

мени

t = n передаточной функцией

Wфq ], которая получается из

Wфp ]

по вы-

ражению

Wфq ] = Wф (p) / T,

(14.1)

где

p = q / T.

и

Непрерывная часть НЧ аналогично также быть представлена передаточ-

ной функцией

W q ]. Объединим ФЭ и НЧ в так называемую приведенную не-

прерывную часть ПНЧ с передаточной функцией

W q ] = Wф (p) Wи (q),

(14.2)

тогда разомкнутая импульсная система в простейшем случае будет представ- лять собой последовательного соединение ПИЭ и ПНЧ (рисунок 14.4), для ко- торой

z (q,) = x (q) W (q,).

(14.3)

Здесь

W (q,) есть

D преобразование Лапласа для импульсной переходной ха-

рактеристики

w (q,) ПНЧ:

W (q,) = D { w n,]} = L: w n,] e qn.

n =0

(14.4)

Отличительной особенностью выражения (14.3) является то, что

x n ]

оп-

ределена лишь для дискретных моментов времени

t = n [аналогично

x (q) = D { x [ n ]}], ] а

z n,] находится для любого момента времени t = n +, 0:::: 1.

Если приведенная непрерывная часть содержить элемент запаздывания (в ФЭ или НЧ), то его передаточная функция равна

ПНЧ

Wф(q) WH(q)

f(t) x(t) ПИ

y1(t)

ФЭ y(t) НЧ

z(t)

W(q)

Рисунок 14.5. Структурная схема замкнутой импульсной системы

e p¢Ñ или

e q¢Ñ, где ¢Ñ = ¢Ñ / T относительное запаздывание. Тогда

W (q,) = e

q¢Ñ

W 0(q,),

(14.5)

где W 0(q,) - передаточная функия ПНЧ без запаздывания. Относительное запаздывание ¢Ñ всегда можно представить в виде

¢Ñ = m + ¢Ñ 1

(14.6)

где m

целое число;

0 < ¢Ñ 1 < 1.

В этом случае

qm

W (q,) = e

W 0(q, ¢Ñ 1)

при ¢Ñ 1 < < 1; (14.7)

W (q,) = e

q (m +1) W (q,1 ¢Ñ 1)

при

0 < < ¢Ñ 1.

(14.8)

Замкнутые импульсные системы во многих случаях могут быть при-

ведены к схеме, аналогичной изображенной на рисунке 14.5, где

f (t) внешнее

воздействие. Для дискретных относительных моментов времени

t = n

x (q) =

f (q) z (q);

(14.9)

z (q) = x (q) W (q),

(14.10)

откуда

x (q) =

f (q) /[1 + W (q)].

(14.11)

Подставив (14.11) в (14.3),получим уравнение движения замкнутой сис- темы в виде

z (q,) =

f (q) W (q,) /[1 + W (q)];

(14.12)

здесь

K (q,) = W (q,) /[1 + W (q)]

(14.13)

- передаточная функция замкнутой импульсной системы;

G (q) = 1 + W (q) = 0

(14.14)

- характеристическое уравнение замкнутой импульчной системы.

Устойчивость

Если известны

f (q) и

K (q,),

то выходная величина

z (n,), может быть

найдена по формуле обращения

z [ n,] = 1

2 ïj

cr c + jï

f f (q) K (q,) eqn

cr c jï

dq.

(14.15)

Решение (14.15) состоит из двух слагаемых:

z (q,) = zвын [ n,] + zcв [ n,],

(14.16)

где

zвын [ n, ] вынужденная составляющая, определяемая видом

f (n);

zcв [ n,] свободная составляющая, определяемая корнями го уравнания (14.14).

qv характеристическо-

Если с течением времени

zcв [ n,] стремится к нулю, т.е.

lim zcв [ n, ] = 0,

n í00

(14.17)

то система называется устойчивой.

Обычно

z cв

[ n, ] =

l

L: C

v =1

v

e q v n,

(14.18)

где l

порядок характеристического уравнения (14.14);

Cv постоянные

коэффициенты, определяемые начальными условиями.

Из (14.18) следует, что условие (14,17) всегда выполняется, если корни

qv имеют отрицательные вещественные части. С учетом периодичности

функции

eq окончательно условия устойчивости формулируются в следующем

виде: система будет устойчивой, если корни qv

характеристического уравне-

ния (14.14) лежат в левой полуплоскости плоскости корней в полосе шириной

2 ï (заштрихованная полоса на рисунке 14.6).

Вычисление корней уравнения (14.14) довольно трудоемкая задача. По- этому для выяснения устойчивости системы аналогично тому, как это делалось для непрерывных систем, пользуются специальными критериями. Ниже рас- сматриваются различные формы критериев устойчивости, которые являются аналогами критериев для непрерывных систем.

Алгебраичесий критерий устойчивости.

Характеристическое уравнение (14.14) можно

Imq

Req

-

Рисунок 14.6. Графическая иллюстрация условий устойчивости в плоскости

q = Re q + j Im q

Рисунок 14.7. Графическая иллюстрация условий устойчивости в плоскости

z = eq = + j�

представить в виде

lq

G (q) = b 0 e

5. b 1 e

(l 1) q

+... + b 1= 0

(14.19)

или, заменяя eq на

z, в виде

l

G (q) = b 0 z

6. b 1 z

l 1

+... + b 1= 0

(14.20)

Отобразим заштрихованную полосу плоскости

q = Re q + j Im q

на рисунок

14.7 в плоскость

z = eq = + j�. Граница этой области найдется из условия

Im q = CO;

z = e jCO

= cos CO + j sin CO = + j�,

откуда

2 + � 2 =

z = 1,

(14.21)

т.е. заштрихованная полоса плоскости q на рисунке (14.7) отображается в круг

единичного радиуса на плоскости

z = eq

(рисунок 14.7).

Таким образом, для устойтивости системы необходимо и достаточно, чтобы корни характеристического уравнения (14.20) лежали внутри заштрихо- ванного круга, т.е. чтобы их модули были меньше единицы:

z < 1.

(14.22)

Существует рад методов, позволяющих найти соотношения между коэф-

фициентами bi

уравнения (14.20), которых выполняется условия (14.22). эту за-

дачу можно решить например, с помощью критерия Гурвица. Для этого отобра- зим круг единичного радиуса плоскости z в левую полуплоскость нового ком- плексного переменного = u + jv. Такое отображение может быть осуществлено преобразованием (рисунок 14.8)

= (z + 1) /(z 1),

(14.23)

откуда

z = (+ 1) /(1).

(14.24)

Рисунок 14.8. Отображение круга единичного радиуса плоскости z в полуплос- кость

Рисунок 14.9. Графическая иллюстрация аналога критерия устойчивости Ми- хайлова

Подставив (14.24) в (14.20), найдем

G () = a l + a l 1+... + a

= 0.

(14.25)

0 1 l

Для уравнения (14.25) можно применить критерий Гурвица и найти гра-

ницу области устойчивости в функции коэффициентов ных с коэффицентами уравнения (14.20).

ai, однозначно связан-

Аналог критерия Михайлова. Подставив в характеристическое уравне-

ние (12.19)

q = jCO,

получим так называемый характеристический вектор

G (jCO) = M (CO) + jN (CO).

(14.26)

При изменении частоты CO от 0 до ï конец этого вектора в комплексной

плоскости

вой.

M (CO) jN (CO) опишит кривую, называемую характеристической кри-

Для устойчивости системы необходимо и доститочно, чтобы при изме- нении частоты CO от 0 до ï характеристическая кривая (14.26), начав свое движение с положительной действительной оси, последовательно прошла 21 квадрантов комплексной плоскости против часовой стрелки (рисунок 14.9), где

l порядок характеристического уравнения (14.19).

Аналог критерия Найквиста. Если в передаточную функцию (14.20)

подставить

q = jCO,

то получим комплексную частотную функцию

W (jCO) = P (CO) + jQ (CO).

(14.27)

сти

При изменеии CO от 0 до ï конец вектора (14.27) в комплексной плоско-

Рисунок 14.10. Графическая иллюстрация аналога критерия устойчивости Найквиста

P (CO) jQ (CO)

Опишет кривую, называемую комплексной частотной характери-

стикой ПНч.

Замкнутая импульсная система, ПНч которой неустойчива, будет ус- тойчива, если разность между числом положительных и отрицательных пе-

реходов характеристикой

W (jCO) отрезка действительной оси от

до 1

(рисунок 14.10, а) будет равна

m / 2, где

m число корней характеристического

уравнения ПНч, находящихся в правой полуплоскости плоскости корней.

В частном случае, когда что соответстует устойчивой ПНЧ, замкнутая

импульсная система будет устойчивой, если

W (jCO) не охватывает точку с коор-

динатами

(1 j 0)

(рисунок 14.10,б.)

Основная литература: 3 [324-348].

Дополнительная литература: 1 [365-414].

Контрольные вопросы:

Замкнутые импульсные системы.

Алгебраичесий критерий устойчивости.

Аналог критерия Михайлова.

Аналог критерия Найквиста.

Конспект лекции №15

Тема лекции: 1.15 Показатели качества регулирования дискретных и им- пульсных систем

Дата добавления: 2015-08-20