
|
Читайте также: |
В реальном процессе регулирования в каждый момент времени величи-
ны x 1, x 2, x 3
имеют вполне определенные значения. Это соответствует вполне
определенному положению точки М в пространстве (рисунок 11.1,а)
С течением времени в реальном процессе величины
x 1, x 2, x 3
опреде-
ленным образом изменяются. Это соответствует определенному перемещению точки М в пространстве по определенной траектории. Следовательно, траек- тория движения точки М может служить наглядной геометрической иллюст- рацией динамического поведения системы в процессе регулирования.
Точка М называется изображающей точкой, ее траектория называется фазовой траекторией, а пространство (x 1, x 2, x 3 ) называется фазовым про- странством.
Так как производные по времени от координат точки представляют проекции ее скорости u на оси координат, то дифференциальные уравнения системы в форме (11.8) представляют собой выраже ния для проекций скоро- сти u; изображающей точки М (рисунок 11.1, а) на оси координат. Следова- тельно, по значениям правых частей уравнений (11.8) в каждый момент вре- мени можно судить о направлении движения изображающей точки М, а вме- сте с тем и о поведении соответствующей реальной системы в процессе регу- лирования.
Начальные условия процесса регулирования (x 10, x 20, x 30 ) определяют
координаты начальной точки фазовой траектории
M 0 (рисунок 16.7, а).
Если переменных в уравнениях (11.8) будет всего две:
x 1 и
x 2 (сис-
тема второго порядка), то изображающая точка будет двигаться не в про- странстве, а на плоскости (фазовая плоскость).
Если переменных будет любое число
n > 3
(система п-го порядка), то
фазовое пространство будет не трехмерным, а n -мерным.
Итак, фазовое пространство и фазовые траектории представляют собой лишь геометрический образ динамических процессов, протекающих в систе- ме. В этом геометрическом представлении участвуют координаты и исклю- чено время. Фазовая траектория сама по себе дает лишь качественное представление о характере поведения системы. Чтобы определить количе- ственно положение изображающей точки (а значит, и состояние системы) в любой момент времени, нужно найти решение заданных дифференциальных уравнений (11.8) во времени.
Если уравнения (11.1) составлены в отклонениях от установившегося
состояния, то последнее характеризуется значениями
x 1= x 2=.... = xn = 0.
Следовательно, изображением установившегося состояния системы являет- ся начало координат фазового пространства.
Отсюда вытекает, что фазовые траектории устойчивой линейной сис- темы будут асимптотически приближаться к началу координат при неограни- ченном увеличении времени. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.
Для нелинейной системы вследствие ряда особенностей процессов, от- мечавшихся выше, фазовые траектории могут принимать самые разнообраз- ные очертания. Если имеется асимптотическая устойчивость для опреде - ленного круга начальных условий, то все фазовые траектории, которые начинаются внутри определенной области, окружающей начало координат фазового пространства (рисунок 11.1, б), будут асимптотически приближать- ся к началу координат. Если устойчивость неасимптотическая, то фазовые траектории, начинающиеся внутри определенной области вокруг начала координат фазового пространства, могут иметь любые очертания, но не бу- дут выходить за пределы некоторой определенной области, окружающей начало координат (рисунок 11.7,б).
Формулировка понятия устойчивости по Ляпунову. Невозмущенное движение (установившийся процесс) называется устойчивым, если при за- данной сколь угодно малой области е (рисунок 11.7, б) можно найти такую область, что при начальных условиях, расположенных внутри этой области, возмущенное движение (переходный процесс) будет таким, что изображающая точка не выйдет из области при любом сколь угодно большом значении вре- мени t.
В аналитической записи формулировка понятия устойчивости по Ляпунову будет следующей. Невозмущенное движение (установившийся процесс) будет устойчивым, если при заданном положительном сколь угодно малом числе можно найти такое положительное число (зависящее от заданного), что при начальных условиях

 xi 0
xi 0
-<
(i = 1,2,..., n)
(11.9)
решение дифференциальных уравнений возмущенного движения (переходно-
го процесса) удовлетворяет неравенствам

 xi -<
xi -<
(i = 1,2,..., n)
при любом сколь угодно большом t.
Представим себе для этой аналитической записи геометрический образ в фазовом пространстве. Очевидно, что при ограничении начальных условий по каждой координате неравенствами (11.9) получается n -мерный куб со стороной 2, внутри которого должна лежать начальная точка фазовой траектории М0 (x 10, x 20,..., xn 0 ). На фазовой плоскости (п = 2) он обращается в квадрат. Анало- гично и второе из написанных неравенств геометрически означает, что фазо-
вые траектории не должны выходить из куба со стороной
2.
В формулировке Ляпунова содержится требование сколь угодной малости указанных областей. Однако практически это определение, так же как и теоре- мы Ляпунова, которые будут приведены ниже, применяется и тогда, когда эти области имеют определенные конечные размеры.
Фазовые траектории для обыкновенных линейных систем. Пусть пере- ходный процесс в некоторой системе описывается уравнением второго поряд- ка
d 2 x
 dt 2
dt 2
+ a dx + a x = 0. (11.10)
 1 dt 2
1 dt 2
Введем обозначение для скорости изменения отклонения регулируемой вели-
чины
y = dx. Тогда уравнение системы (11.10) преобразуется к виду
 dt
dt

|
(11.11)
 dx = y. 1
dx = y. 1
dt 1J
Исключим из уравнений (11.10) время t, разделив первое из них
на второе (при х и
y � 0):
 dy = a dx 1
dy = a dx 1
x
 a 2.
a 2.
y
(11.12)
Решение
y = <ð (x)
этого дифференциального уравнения с одной произ-
вольной постоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (х, у), каждая из которых соот- ветствует одному определенному значению произвольной постоянной.
Вся совокупность интегральных кривых представит собой все возмож- ные фазовые траектории, а значит, и все возможные виды переходного про- цесса в данной системе автоматического регулирования при любых началь- ных условиях.
Рассмотрим отдельно различные случаи. Уравнению (11.10) соответст- вуют корни характеристического уравнения
 p = a 1±
p = a 1±
1, 2 2

|
причем возможны шесть случаев:
1) корни чисто мнимые при вости линейной системы);
a 1= 0,
a 2> 0
(граница устойчи
2)
|
ные части при стема);
1 a 1> 0,
a 2 > 0
(устойчивая линейная си
3) корни комплексные и имеют положительные вещественные
|
a 1-< 0,
a 2> 0 (неустойчивая линейная система);
4) корни вещественные отрицательные при тойчивая линейная система);
5) корни вещественные положительные при
устойчивая линейная система);
a 1 > 4 a 2,
a 1> 0,
a 1-< 0,
a 2 > 0
a 2> 0
(ус-
(не-
6) корни вещественные и имеют разные знаки при
a 2 > 0
(неустой-
чивая линейная система); в частности, один из корней будет равен нулю
при
a 2 = 0
(граница устойчивости линейной системы).
Основная литература: 3 [324-348].
Дополнительная литература: 1 [365-414].
Контрольные вопросы:
1. Основные понятия о фазовой плоскости.
2. Что такое фазовая плоскость?
3. Что такое фазовая траектория?
4. Что такое фазовое пространство?
Конспект лекции №12
Тема лекции: 12. Фазовые портреты нелинейных систем.
Состояния равновесия. В фазовых пространствах линейных систем име- ется одна особая точка (при принятой выше системе отсчета - начало коорди- нат), которая может быть либо устойчивой, либо неустойчивой точкой равнове- сия.
В нелинейных системах может быть несколько особых точек, часть из ко- торых может относиться к устойчивым, другая часть - к неустойчивым точкам равновесия. Кроме того, в фазовых пространствах могут иметь место бесчис- ленные множества точек равновесия - отрезки покоя и даже области покоя.
Неоднородность топологической структуры фазовых пространств. То- пологическая структура фазовых пространств линейных систем однородна в том смысле, что единственная особая точка является либо центром притяжения всех фазовых траекторий, либо центром их отталкивания, либо нейтральным центром, окруженным замкнутыми траекториями, заполняющими все про- странство. В первом случае все фазовое пространство является областью ус- тойчивости, во втором - все оно представляет собой область неустойчивости. Ограниченных областей устойчивости или неустойчивости в фазовых про- странствах линейных систем нет.
В нелинейных системах фазовое пространство может оказаться разделен- ным на ряд областей. Часть из этих областей, в которых фазовые траектории скручиваются к некоторой особой точке или области, можно рассматривать как области устойчивости; часть из них, где особая точка служит центром отталки- вания траекторий, будет относиться к областям неустойчивости. Как мы ви- дели, фазовые траектории могут также стремиться к замкнутым
кривым - «накручиваться» на устойчивые предельные циклы «скручиваясь» с неустойчивых. В рассмотренных выше примерах предельный цикл был один, но их может быть и несколько.
Рассмотрим в качестве иллюстрации два фазовых портрета, показанных на рисунок 12.1.
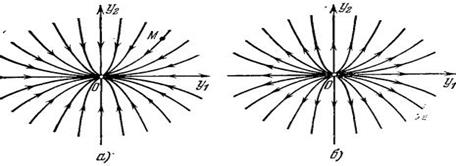
Рисунок 12.1
На рисунок 12.1, начало координат неустойчиво, предельный цикл устой- чив. В этой системе не может быть состояния равновесия. Под влиянием ма- лейших флуктуации мы из начала координат выходим на предельный цикл: в данной системе автоколебания возбуждаются без специально приложенного внешнего воздействия. Таким фазовым портретом обладают генераторы с мяг- ким возбуждением автоколебаний. Примером может служить релейная система с зоной нечувствительности, если при определенном выборе параметров и ра- зомкнутом реле система неустойчива.
На рисунок 12.1, б устойчивая точка равновесия окружена двумя пре- дельными циклами: внутренний цикл неустойчив, внешний - устойчив. Если к
системе приложен слабый толчок такой величины, что начальные значения
x 0 и
x 0¢ не выходят за пределы внутренней области неустойчивого предельного цик- ла, мы попадаем на траекторию, скручивающуюся к началу координат. Система приходит в колебательный режим, но колебания затухают. Если же внешний
толчок достаточно велик для того, чтобы вывести начальную точку за пределы внутреннего неустойчивого цикла, то мы попадаем на траекторию, накручи- вающуюся на внешний устойчивый цикл, и в системе возникают автоколеба- ния. Таким фазовым портретом обладают генераторы, с жестким возбуждением колебаний. При определенном подборе параметров колебания могут возник- нуть, например, в релейной системе с зоной нечувствительности, если при ра- зомкнутом реле система устойчива. Примером подобных генераторов могут служить стенные часы с маятником, которые не начинают ходить от слабого толчка, или же плохо настроенный микрофон с репродуктором, возбуждаю- щиеся от резкого повышения голоса оратора.
Особые траектарии. На фазовой плоскости области с различной тополо- гической структурой разграничиваются линиями, которые также являются фа- зовыми траекториями и называются особыми фазовыми траекториями. Особы- ми, «водораздельными» фазовыми траекториями могут быть, как мы видели, предельные циклы. Но разделяющие траектории могут быть и незамкнутыми. В этих случаях они называются сепаратрисами. На рисунок 12.2 показан пример сепаратрисы, разделяющей области затухающих колебаний и выпадения из синхронизма синхронного двигателя, описываемого следующими уравне- ниями.
dy = 2 hy k sin x + M,
dx = y,
dt y dt
где М = const, h и k - коэффициенты пропорциональности.
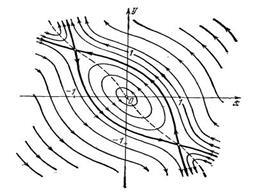
Рисунок 12.2
В фазовом пространстве кривые уже не могут быть границами областей с различной топологической структурой. Последние разграничиваются сепарат- рисными поверхностями, целиком состоящими из особых фазовых траекторий. Основная литература: 3 [324-348].
Дополнительная литература: 1 [365-414].
Контрольные вопросы:
1. Точка равновесия.
2. Неоднородность топологической структуры фазовых пространств.
3. Особые траектарии фазовой плоскости.
Конспект лекции №13
Тема лекции: 1.13 Дискретные и импульсные АСР. Дискретные функции. Структура дискретных АСР
Основные понятия и определения
Дискретными называются системы, в которых осуществляется передача и преобразование сигналов, квантованных по уровню или по времени. Квантова- ние по уровню соответствует замене действительного значения преобразуемого сигнала в любой момент времени его дискретным значением, кратным целому числу уровней квантования. Квантование по времени соответствует замене не- прерывного во времени сигнала его значениями в дискретные равноотстоящие моменты времени. В зависимости от вида квантования различают следующие дискретные АСР.
a) релейные, в которых происходит квантование по уровнию; это как пра-
вило, нелинейные системы;
б) импульсные, в которых происходит квантование по времени; эти сис-
темы рассматриваются в настоящем разделе;
в) цифровые, в которых происходит квантование по уровню и времени;
при малых значениях квантуемого сигнала, когда квантование по уровню ска- зывается существенно, цифровая система сводится к релейной; при больших значениях квантуемого сигнала, когда дискретностью по уровню можно пре- небречь,цифровая система сводится к импульсной.
В импульсных системах квантование по времени осуществляется им- пульсным элементом (ИЭ), выходная величина которого представляет собой модулированную последовательность импульсов (рисунок 13.1). Различают следующие типы импульсной модуляции (рисунок 13.2):
а) амплитудно – импульсную модуляцию (АИМ), при которой изменяется
амплитуда А выходных импульсов в зависимости от значений входной величи- ны в дискретные равноотстоящие на величину Т моменты времени;
б) широтно – импульсную модуляцию (ШИМ), при которой изменяется
ширина импульса ó Т в зависимости от значений входной величины в дискрет- ные равноотстоящие моменты времени;
в) время-импульсную модуляцию (вИМ), которой соответствует опреде-
ленный временной сдвиг Т
импульса постоянной формы в зависимости от
значения входной величины в дискретные равноотстояшие моменты времени.
Каждый тип модуляции характеризуется так называемой крутизной ха- рактеристики ИЭ:
kАИМ
= А / x;
kШИМ
= óT / x;
kвИМ
= T / x. (13.1)
Если величина k постонна и не зависит от x, то импульсный элемент ли- нейный, если и непрерывная часть (рисунок 13.1) линейна, то система называ- ется линейной импульсной.
Дискретные функции
При исследовании автоматических систем регулирования приходится иметь дело с дискретной последовательностью промоугольных импульсов раз- личной амплитуды и делительности. Описание процессов в таких системах производится с помощью специальных дискретных функций: решетчатых и смещенных решетчатых (рисунок 13.1).
Решетчатой называется такая функция, значения которой определены лишь в дискретные, равноотстоящие моменты времени. В отличие от непре-
рывной функций
x nT ], и по определению
x nT ] = x (t) при
t = nT, (13.2)
где T - интервал дискретизации по времени;
n любое целое число.
Смещенная решетчатая функция
x (t)
соответствует одна – единственная
решетчатая функция вовать различные
x nT ], обратное же решетчатой функции могут соответст-

Рисунок 13.1. Непрерывная функция
(а)
и соответствующие ей решетча-
тая
(б) и смещенная решетчатая
(в) функции

Рисунок 13.2. Рашетчатая функция и ее отибающие

Рисунок 13.3. Первая разность решетчатой функции
непрерывные (и даже разывные) функции, если только их ординаты в дискрет-
ные моменты времени
t = nT
равны ординатам (дискретам) решетчатой функ-
ции. Эти функции называются огибающими решетчатой функции (штриховые линии на рисунки 13.2).
Исследовать решетчатые функции удобнее в относительном масштабе времени

 тогда
тогда
t = t / T; = Ë t / T, (13.4)
 x n ] = x (t)
x n ] = x (t)
при
t = n; (13.5)


t 1= n +. (13.6)
Скорость изменения решетчатой функции характеризуется ее первой раз- ностью (рисунок 13.3), или разностью первого порядка
Ë х n ] = x n + 1] x n ]. (13.7)
Разность второго порядка
Ë2 x n ] = Ë x n + 1] Ë x n ] = x n + 2] 2 x n + 1]+ x n ]. (13.8)
Разность
k го порядка
k
Ë kx n ] = Ë k 1 x n + 1] Ë k 1 x n ] = L:(1) v
v = 0
k!
 v!(k v)!
v!(k v)!
x n + k v ]. (13.9)
Во многих случаях поведение дискретных автоматических систем можно описать линейными разностными уравнениями с постоянными коэффициента- ми в форме
bk Ë y n ]+ bk 1Ë
y n ]+... + b 0 y n ] = x n ].
(13.10)
k k 1
Здес правая часть уравнения является известной заданной функцией
x n ],
и y n ]- искомой функцией, представляющей собой решение разностного урав-
нения.
Если в (13.10) заменить разности решетчатой функции
y n ]
их значения-
ми по (13.9), то получится иная форма записи разностного уравнения:
|
k 1
y n + k 1]+... + a
y n ] = x n ].
(13.11)
ak 1
l
= L: bk l v = 0
(1) lv
(k v)!;
 (l v)!(k l)
(l v)!(k l)
(13.12)
l
 b = a
b = a
(k v)!;
(13.13)
k 1
L:
v =0
k l (l v)!(k l)
Решение разностных уравнений вида (13.10), (13.11) значительно упро- щается, если воспользоваться дискретными преобразованием Лапласа. Осно- ванные этапы решения сводятся к следующим:
 функции
функции
y n ] и
x n ]
вещественной переменной n преобразуются в
функции
y q ] и
x q ]
комплексной переменной
q = cr + jCO, называемой парамет-
ром преобразования;
находится решение для функции
y q ];
найденное решение для
y q ] преобразуется в
y n ].
Дискретное преобразование Лапласа для решетчатых функций определя- ется соотношением
x (q) = L: e qnx (n).
n = 0
(13.14)
Для смещенных решетчатых функций
x (q) = L: e qn x n,].
n =0
(13.15)
Так как папаметр не влияет на свойства дискретного преобразования
Лапласа, то в дальнейшем рассматривается лишь функция
x n ].
Если для функции
x n ]
можно указать такие зависящие от n постоянные
a и b, что при любом
n > 0 выполняется неравенство

 x n ] < aebn, (13.16)
x n ] < aebn, (13.16)
то ряд (13.14) сходится при всех cr с < b, где cr c - абсцисса сходимости.
Помимо одностороннего дискретного преобразования Лапласа (13.14)
вводится двустороннее дискретное преобразование Лапласа
x (q) =
L: e qn x n ].
n = 00
(13.17)
Если при
n < 0
x n ] = 0, то двустороннее дискретное преобразование Лап-
ласа сводится к одностороннему, которое и рассматривается в дальнейшем, ес- ли нет специальных оговорок.
Если в (13.14) положить
z = eq, (13.18)
то
x (z) = L: z n x n ].
n = 0
(13.19)
называется
z преобразованием.
Пример 13.1. Пусть
x n ] = 1 n ],
тогда
x (q) = L: e qn 1
n =0
eq
 .
.
eq 1
Рассмотрим основные свойства дискретного преобразования Лапласа.
Для сокращения вместо (13.14) будем использовать символическую запись
x (q) = D { x n ]}; (13.20)
x (q) = D { x n ]}
(13.21)
Линейность преобразования. Если
x (q) = D { x n ]};
1 1
...........................
x (q) = D { x n ]},
v v
то
v v l
L: aixi (q) = D íL: aixin ],
(13.22)
i =1
l i =1 J
где
ai
постоянные величмны.
Аналогично если
x 1(q) = D
Дата добавления: 2015-08-20; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Конспект лекции №1 4 страница | | | Конспект лекции №1 6 страница |