Сравнение б. м. и б. б. функций.
Понятие сложной функции. | Понятие обратной функции. | Некоторые важнейшие функциональные зависимости. | Тригонометрические и обратные тригонометрические функции. | Преобразование графиков функций. | Определение предела функции в точке. | Основные теоремы о пределах функций. | Замечательные пределы. | Второй замечательный предел. | Бесконечно малые (б.м.) и бесконечно большие (б.б.) функции. |
Пусть a (х), b (х) – б. м. при 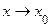 , т.е.
, т.е.  и
и 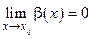 .
.
1. Если 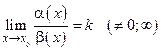 , то a (х) и b (х) называются б. м. одного порядка.
, то a (х) и b (х) называются б. м. одного порядка.
2.
 Если
Если  = 1, то a (х) и b (х) называются эквивалентными бесконечно малыми. Записываем это так: a (х) b (х).
= 1, то a (х) и b (х) называются эквивалентными бесконечно малыми. Записываем это так: a (х) b (х).
3. Если  =0, то a (х) называется б.м. более высокого порядка, чем б.м. b (х) (еще говорят, что a (х) имеет более высокий порядок малости, чем b (х), при х ® х 0) записываем это так: a (х)=
=0, то a (х) называется б.м. более высокого порядка, чем б.м. b (х) (еще говорят, что a (х) имеет более высокий порядок малости, чем b (х), при х ® х 0) записываем это так: a (х)=  (b (х)). Символ
(b (х)). Символ  читается "0 малое".
читается "0 малое".
4. Если 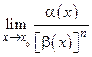 = А (¹0; ¥), то a (х) называется бесконечно малой порядка n относительно b (х).
= А (¹0; ¥), то a (х) называется бесконечно малой порядка n относительно b (х).
 Аналогичные определения имеют место и для б.б. функций. В частности, если А (х) и В (х) – б.б. при х ® х 0, т.е.
Аналогичные определения имеют место и для б.б. функций. В частности, если А (х) и В (х) – б.б. при х ® х 0, т.е.  ¥ и
¥ и 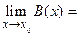 ¥, то они называются эквивалентными б.б. при х ® х 0, если
¥, то они называются эквивалентными б.б. при х ® х 0, если  1. Пишем А (х) В (х)
Так если Рп (х) = а0хп + а1хп-1 +... + ап-1х + ап – многочлен степени п, то
1. Пишем А (х) В (х)
Так если Рп (х) = а0хп + а1хп-1 +... + ап-1х + ап – многочлен степени п, то

Рп (х) = а0хп (1+  +... +
+... +  ) а0хп.
) а0хп.

Важнейшие эквивалентности, используемые при вычислении пределов:



 1. sin x x, 3. ex – 1 x;
1. sin x x, 3. ex – 1 x;


2. ln (1 + x) x, 4. (1 +x)a - 1 a x, a >0.
Это запись первого, третьего, четвертого и пятого замечательного предела на языке эквивалентных б. м.
Рассмотрим применение эквивалентных б. м. и б. б. к вычислению пределов.
 Теорема 16.5. Пусть a1(х), a2(х), b1(х), b2(х) – б. м. функции при
Теорема 16.5. Пусть a1(х), a2(х), b1(х), b2(х) – б. м. функции при 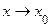 и a1(х) a2(х), b1(х) b2(х). Тогда справедливо равенство
и a1(х) a2(х), b1(х) b2(х). Тогда справедливо равенство 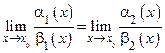 (16.3)
(16.3)
 Доказательство. a1(х) a2(х) Þ
Доказательство. a1(х) a2(х) Þ 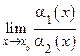 =1, b1(х) b2(х) Þ
=1, b1(х) b2(х) Þ 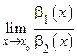 =1.
=1.
Тогда  .
.

 Для эквивалентных б. б. функций справедлива формула, аналогичная формуле (16.3).
Для эквивалентных б. б. функций справедлива формула, аналогичная формуле (16.3).
Это означает, что при вычислении пределов частного и произведения функций одну б. м. (б. б.) можно заменить на другую б. м. (б. б.), эквивалентную первой.
 Пример 16.11.
Пример 16.11. 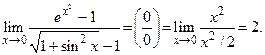


 Пояснение. Так как ex -1 x, то
Пояснение. Так как ex -1 x, то  x2.
x2.


 Далее: (1+ х) a -1 a х Þ
Далее: (1+ х) a -1 a х Þ  -1
-1  ,
,
sin x x Þ sin2x x2 Þ  -1
-1 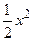 .
.
Затем применили теорему 16.5.
Дата добавления: 2015-07-20; просмотров: 72 | Нарушение авторских прав
mybiblioteka.su - 2015-2024 год. (0.007 сек.)

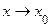 , т.е.
, т.е.  и
и 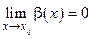 .
.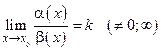 , то a (х) и b (х) называются б. м. одного порядка.
, то a (х) и b (х) называются б. м. одного порядка. Если
Если  = 1, то a (х) и b (х) называются эквивалентными бесконечно малыми. Записываем это так: a (х) b (х).
= 1, то a (х) и b (х) называются эквивалентными бесконечно малыми. Записываем это так: a (х) b (х).
 =0, то a (х) называется б.м. более высокого порядка, чем б.м. b (х) (еще говорят, что a (х) имеет более высокий порядок малости, чем b (х), при х ® х 0) записываем это так: a (х)=
=0, то a (х) называется б.м. более высокого порядка, чем б.м. b (х) (еще говорят, что a (х) имеет более высокий порядок малости, чем b (х), при х ® х 0) записываем это так: a (х)=  (b (х)). Символ
(b (х)). Символ  читается "0 малое".
читается "0 малое".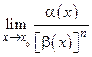 = А (¹0; ¥), то a (х) называется бесконечно малой порядка n относительно b (х).
= А (¹0; ¥), то a (х) называется бесконечно малой порядка n относительно b (х). Аналогичные определения имеют место и для б.б. функций. В частности, если А (х) и В (х) – б.б. при х ® х 0, т.е.
Аналогичные определения имеют место и для б.б. функций. В частности, если А (х) и В (х) – б.б. при х ® х 0, т.е.  ¥ и
¥ и 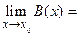 ¥, то они называются эквивалентными б.б. при х ® х 0, если
¥, то они называются эквивалентными б.б. при х ® х 0, если  1. Пишем А (х) В (х)
1. Пишем А (х) В (х)

 +... +
+... +  ) а0хп.
) а0хп.




 1. sin x x, 3. ex – 1 x;
1. sin x x, 3. ex – 1 x;

 Теорема 16.5. Пусть a1(х), a2(х), b1(х), b2(х) – б. м. функции при
Теорема 16.5. Пусть a1(х), a2(х), b1(х), b2(х) – б. м. функции при 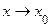 и a1(х) a2(х), b1(х) b2(х). Тогда справедливо равенство
и a1(х) a2(х), b1(х) b2(х). Тогда справедливо равенство 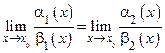 (16.3)
(16.3)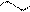
 Доказательство. a1(х) a2(х) Þ
Доказательство. a1(х) a2(х) Þ 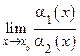 =1, b1(х) b2(х) Þ
=1, b1(х) b2(х) Þ 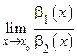 =1.
=1.
 .
.
 Для эквивалентных б. б. функций справедлива формула, аналогичная формуле (16.3).
Для эквивалентных б. б. функций справедлива формула, аналогичная формуле (16.3).
 Пример 16.11.
Пример 16.11. 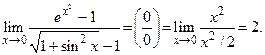


 Пояснение. Так как ex -1 x, то
Пояснение. Так как ex -1 x, то  x2.
x2.


 Далее: (1+ х) a -1 a х Þ
Далее: (1+ х) a -1 a х Þ  -1
-1  ,
,
 -1
-1 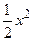 .
.