Действия над векторами в координатной форме.

Рассмотрим в пространстве ортонормированный базис , , . Пусть далее

= х₁ + у₁ + z₁ , = х₂ + у₂ + z₂ .

Сложение векторов: при сложении векторов их соответствующие координаты складываются, т.е.

+ =(х₁+х₂) +(у₁+у₂) +(z₁+z₂) = { х₁+х₂; у₁+у₂; z₁+z₂ }

Действительно, ( + ) _х = ПР_х ( + ) = ПР_х + ПР_у = х₁+х₂.

Аналогично для остальных координат.

Умножение вектора на число: при умножении вектора на число координаты вектора умножаются на это число, т. е.

.

Равенство векторов: два вектора = х₁ + у₁ + z₁ и = х₂ + у₂ + z₂ равны тогда и только тогда, когда равны их соответствующие координаты: т.е. х₁ = х₂, у₁ = у₂, z₁ = z₂.

Коллинеарность векторов: || ó =λ , или в координатной форме

х₁ + у₁ + z₁ =λ(х₂ + у₂ + z₂ )=(λх₂) +(λ у₂) +(λ z₂) ,

отсюда х₁=λх₂, у₁=λу₂, z₁=λz₂, т.е. .

Вывод: коллинеарность векторов равносильна пропорциональности соответствующих координат этих векторов.

Координаты вектора через координаты его начала и конца: если = и известны координаты точек А (х_1;у_1;z₁) и В (х_2;у_2;z₂). Тогда (см. рис. 3.19)

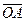= – ={ х₂; у₂; z₂ } – { х₁; у₁; z₁ } = { х₂- х₁; у₂- у₁; z₂- z₁ }.

= { х₂- х₁; у₂- у₁; z₂- z₁ }.

Мы воспользовались тем, что, если дана точка М (х,у,z), то вектор 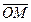{ х,у,z } (см. рис. 22). Вектор 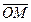называется радиусом– вектором точки М.

Дата добавления: 2015-07-20