
Читайте также:
|
1) Вычислить 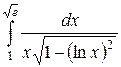 .
.
Решение. Сделаем замену  , тогда
, тогда 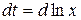 ;
;  ;
;  ;
;  . Новые пределы интегрирования находим из соотношения
. Новые пределы интегрирования находим из соотношения  ; если
; если  , то
, то  ; если
; если  , то
, то  . Таким образом, изменению переменной от
. Таким образом, изменению переменной от  до
до  соответствует изменение переменной
соответствует изменение переменной  от
от  до
до  . Поэтому
. Поэтому



2) Вычислить  .
.
Решение. Положим  ,тогда
,тогда  ;
; 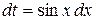 ;
;  . Новые пределы интегрирования находим из соотношения
. Новые пределы интегрирования находим из соотношения  ; если
; если  , то
, то  ; если
; если  , то
, то  . Таким образом, изменению переменной x от
. Таким образом, изменению переменной x от  до x =2 соответствует изменение переменной
до x =2 соответствует изменение переменной  от
от  до
до  . Следовательно,
. Следовательно,

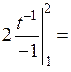

3)Вычислить  .
.
Решение. Положим  , тогда
, тогда  ;
;  ;
;  . Новые пределы интегрирования находим из соотношения
. Новые пределы интегрирования находим из соотношения  ; если
; если  , то
, то  ; если
; если  , то
, то 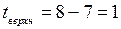 . Таким образом, изменению переменной
. Таким образом, изменению переменной 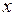 от
от  до
до  соответствует изменение переменной
соответствует изменение переменной  от
от 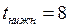 до
до  , следовательно,
, следовательно,

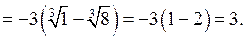
Контрольные варианты к задаче 2.
ЗАДАНИЕ. Вычислить определенные интегралы:
1. 1)  ; 2. 1)
; 2. 1)  ;
;
2)  ; 2)
; 2)  ;
;
3)  3)
3)  .
.
3. 1)  ; 4. 1)
; 4. 1)  ;
;
2)  ; 2)
; 2)  ;
;
3  . 3)
. 3) 
 .
.
5. 1)  ; 6. 1)
; 6. 1) 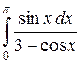
2) 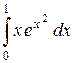 ; 2)
; 2)  ;
;
3)  . 3)
. 3)  .
.
7. 1)  ; 8. 1)
; 8. 1)  ;
;
2) 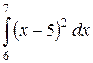 ; 2)
; 2)  ;
;
3)  . 3)
. 3) 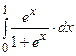 .
.
9. 1)  ; 10. 1)
; 10. 1)  ;
;
2) 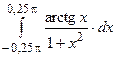 ; 2)
; 2)  ;
;
3)  . 3)
. 3)  .
.
11. 1) 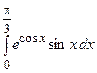 ; 12. 1)
; 12. 1)  ;
;
2)  ; 2)
; 2)  ;
;
3)  . 3)
. 3)  .
.
13. 1)  ; 14. 1)
; 14. 1)  ;
;
2)  ; 2)
; 2)  ;
;
3)  3)
3)  .
.
15. 1)  ; 16. 1)
; 16. 1)  ;
;
2) 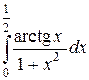 ; 2)
; 2)  ;
;
3)  . 3)
. 3) 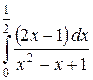 .
.
Как было показано выше с помощью определенного интеграла можно вычислять площади плоских фигур, ограниченных кривыми. Напомним, что кривые могут быть заданы различными способами:
а) если фигура представляет из себя криволинейную трапецию вида.

  
  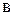  Рисунок 4
Рисунок 4
| Тогда её площадь вычисляется по формуле:
 ; ;
|
б) если криволинейная трапеция расположена ниже оси  , т.е.
, т.е.  тогда исходя из свойств определенного интеграла
тогда исходя из свойств определенного интеграла
Рисунок 5 |
 . .
|
В общем случае  ;
;
в) если плоская фигура имеет сложную форму, т.е. прямые  «вырождаются» в точки, то фигуру следует разбить на части так, чтобы можно было применить известные формулы.
«вырождаются» в точки, то фигуру следует разбить на части так, чтобы можно было применить известные формулы.
Проиллюстрируем некоторые возможные варианты:
 

  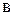 
 Рисунок 6
Рисунок 6
|
 ; ;
|
г) если криволинейная трапеция ограничена прямыми  и
и
 , осью
, осью  и непрерывной кривой
и непрерывной кривой  , то
, то 
 
 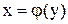

  Рисунок 7
Рисунок 7
|
 . .
|
Задача 3. 1) Вычислить площадь фигуры, ограниченной параболой  и прямой
и прямой 
Дата добавления: 2015-10-21; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определенный интеграл и его геометрический смысл | | | Решение |