Рассмотрим двухшаговый метод наименьших квадратов ДМНК.

Будем так же предполагать, что проблема идентификации в уравнениях модели преодолена и все они идентифицируемые. При этом часть из них являются сверх идентифицируемыми. На первый план при идентификации сверх идентифицируемых моделей выступает проблема авторегрессионности. Если подобрать инструментальные переменные, то эта проблема будет преодолена.

Вопрос, как построить такие переменные.

Вернемся к элементарной макромодели Кейнса (9.18):

(9.18)

Приведенная форма модели для эндогенной переменной имеет вид:

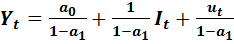(9.19)

Для удобства перепишем уравнение (9.19) в виде:

(9.39)

Здесь m₀ и m₁ значения параметров приведенной формы уравнения (9.19).

Наличие в (9.39) случайного возмущения приводит к авторегрессионности первого уравнения системы (9.18). Если бы удалось избавиться от случайного возмущения в уравнении (9.39), то пропадет корреляционная связь между регрессором и случайным возмущением . Вычтем из правой и левой частей уравнения (9.39) величину :

(9.40)

Правая часть (9.40) представляет собой оценку (прогноз) значения эндогенной переменной , если известны значения оценок параметров приведенной формы уравнения (9.39):

(9.41)

В результате получили, что переменная имеет все необходимые свойства инструментальной по отношению к переменной : они тесно коррелируют между собой, но при этом не коррелирует со случайным возмущением .

Отсюда вытекает алгоритм двухшагового метода наименьших квадратов.

Шаг 1. Модель приводится к приведенной форме.

Шаг 2. Для текущей эндогенной переменной, которая участвует в сверх идентифицируемом уравнении в качестве регрессора, по имеющейся выборке наблюдений оцениваются параметры приведенной формы уравнения для этой переменной с помощью МНК.

Шаг 3. С помощью оцененной формы уравнения модели рассчитываются прогнозные значения эндогенной переменной для всех точек выборки.

Шаг 4. С помощью МНК оцениваются структурные параметры сверхидентифицированного уравнения модели, ипользуя в качестве регрессора оцененные значения вместо реальных значений переменной .

В результате, на основании теоремы о применении инструментальных переменных, будут получены состоятельные оценки структурной формы поведенческих уравнений в моделях в виде систем одновременных уравнений.

Замечание. Двухшаговый метод наименьших квадратов применим как для идентификации сверх идентифицируемых уравнений модели, так и для идентификации точно идентифицируемых уравнений модели.

Пример. Оценить параметры структурной формы модели:

(9.42)

Здесь: , - текущие эндогенные переменные;

, , -экзогенные переменные.

Исходные данные для идентификации модели (9.42) приведены в таб. 9.2.

Таблица 9.2.

Решение.

Шаг 1. Проверяем модель на идентифицируемость уравнений.

Расширенная матрица коэффициентов модели (9.42):

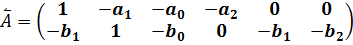
Ограничения на уравнения модели:

Для первого уравнения модели:

Правило ранга:

Правило порядка: K =4, K₁ =2, G₁ =2; K- K₁=4-2=2> G₁-1=1

Вывод: первое уравнение модели сверх идентифицированное.

Для второго уравнения имеем:

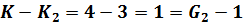
Вывод: второе уравнение системы (9.42) точно идентифицированное.

Шаг.2 Оценивание параметров приведенной формы модели (9.42):

Приведенная форма модели имеет вид

(9.44)

Оценка модели (9.42) по данным таб. 9.2 дала результат:

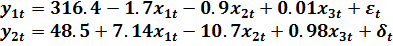(9.45)

Шаг 3. Для оценки параметров первого уравнения модели (9.42) для каждого наблюдения таб. 9.2 вычислим с помощью второго уравнения системы (9.45) значения оценки , тав. 9.3.

За тем, используя столбцы , оцениваем первое уравнение модели (9.41), которое принимает вид (9.46).

Второе уравнение модели (9.41) можно оценить как КМНК, так ДМНК, т.к оно является точно идентифицированным.

Таблица 9.3.

(9.46)

Оценим его также с помощью ДМНК. Для этого с помощью первого уравнения модели 9.44 вычислим оценку эндогенной переменной .

Таблица 9.4

Используем ее в качестве регрессора для оценки второго уравнения (9.41)

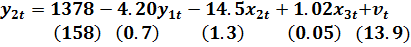(9.47)

В результате мы оценили оба уравнения модели (9.42).

Заметим, что ошибки параметров модели, формально говоря, приведены не точно. Они должны быть скорректированы в связи с тем, что в качестве регрессоров были использованы оценки эндогенных переменных.

---

Дата добавления: 2015-10-29