Подводим итог.

1. Рассмотрены два метода получения наилучшего прогноза по линейной модели множественной регрессии.

2. Дано определение доверительного интервала.

3. Рассмотрено понятие адекватности модели.

4. Сформулирована статистическая гипотеза для проверки модели на адекватность.

5. Подробно на конкретном примере обсужден весь комплекс построения и анализа модели линейной множественной регрессии.

Вопросы для самоподготовки.

1. Определение адекватности.

2. Как вычисляется наилучший прогноз эндогенной переменной по оцененной модели множественной линейной регрессии.

3. Как вычисляется значение стандартной ошибки прогноза.

4. Как рассчитываются границы доверительного интервала.

5. Какова последовательность действий при проверке адекватности линейной модели множественной регрессии.

6. С какой целью формируется контрольная выборка.

7. С какой целью формируется обучающая выборка.

8. Как формируется обучающая выборка.

9. Способы тестирования модели на адекватность.

10. В каком случае принимается гипотеза об адекватности модели.

Лекция 7. Применение фиктивных переменных в эконометрических

Моделях

Содержание лекции:

1. Понятие фиктивной переменной

2. Фиктивные переменные сдвига и примеры их применения

3. Фиктивные переменные наклона

Мы завершили рассмотрение содержания всех этапов построения эконометрических моделей.

Вспомним, что в самом начале было выдвинуто ограничение о том, что рассмотрению подлежат только модели в виде линейных алгебраических уравнений. Предполагалось также, что в моделях содержатся только непрерывные переменные. Такие модели часто называют эконометрическими моделями с постоянной структурой. При построении таких моделей предполагается, что взаимосвязи между зависимой и независимыми переменными постоянны и не подвержены изменениям ни во времени, ни в пространстве.

Однако кроме переменных, включенных в спецификацию модели, на значение анализируемого показателя обычно влияет большое число сопутствующих факторов.

При анализе реальных социально-экономических процессов часто оказывается, что со временем под влиянием вновь появившихся условий, факторов и масштаба взаимосвязи между переменными объекта изменяются.

В таких случаях модели с постоянной структурой становятся недостаточно точными для объяснения закономерностей меняющихся явлений. Для их анализа прибегают к построению моделей, которые получили название моделей с переменной структурой.

Если в ходе сбора статистических данных имеет место косвенное воздействие на них качественных факторов (переменных), то линейные

модели с переменной структурой учитывают скачкообразные сдвиги в

значениях параметров модели.

Чаще всего предполагают, что сопутствующие факторы носят качественный характер.

Примеры. Моделирование влияния пола специалистов на уровень зарплаты.

Моделирование доходов граждан от типа учебного заведения, в котором он получил образование (государственное, частное, специализированное).

Модель инфляции с учетом различных видов регулирования со стороны государства.

За качественными переменными скрывается целый комплекс факторов: изменение длины светового дня, среднемесячной температуры воздуха, изменение климатических условий и т.п. При анализе расходов на продукты питания необходимо иметь в виду различия в образе жизни городского и сельского населения.

Для учета влияния качественных факторов привлекают переменные, которые получили название фиктивных.

Фиктивные переменные, как правило, принимают только два значения: ноль и единица. Фиктивная переменная имеет значение «1» для конкретной части выборочных значений и «0» для всей оставшейся совокупности данных.

Возможны два подхода решения задачи моделирования поведения объекта, на значения переменных которого оказывают влияние качественные факторы:

- построить несколько моделей отдельно для каждого значения (градации) качественной переменной

- учесть влияние качественного фактора в одной модели.

Например, необходимо построить модель уровня заработной платы сотрудников в зависимости от стажа работы и от его пола (мужчина/женщина). Естественно, можно разделить собранные статистические данные на две части: отдельно для мужчин, отдельно для женщин, и построить две независимые линейные модели. Однако по ряду причин более перспективным считается построение одной общей модели, как для мужчин, так и для женщин. В этом случае, анализируя оцененную модель, легко сделать вывод о статистической значимости на уровень зарплаты для мужчин и женщин при одинаковом стаже работы.

Обсудим, как решается эта задача с помощью фиктивных переменных.

Рассмотрим пример построения модели величины расходов на обучение в зависимости от числа учащихся в обычных (общеобразовательных) и специализированных школах. Будем предполагать, что в обоих типах школ зависимость расходов на обучение имеет одинаковую зависимость от числа учащихся.

Введем для идентификации типа школы фиктивную переменную в виде:

Спецификацию модели запишем в следующем виде:

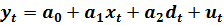(7.1)

В спецификации (7.1) участвуют обе переменные: непрерывная x_t (количество учащихся) и фиктивная, имеющая дискретный характер, d_t.

Отметим, что значение d=1 можно было присвоить и для общеобразовательной школы. На построение модели это влияния не окажет.

Модель (7.1) позволяет легко получить независимые модели для различных типов школ. Для этого достаточно присвоить одно из ее возможных значений:

для общеобразовательной школы имеем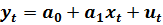

для специализированной

Полученные модели отличаются только значением свободного коэффициента.

Рассмотрим пример построения модели зависимости затрат на

обучение в общеобразовательных и специализированных школах в Шанхае (по данным Доугерти [3]). Спецификация модели имеет вид (7.1). Оцененная модель (7.1) получила следующий вид:

(7.2)

Из (7.2) видно, что модель имеет качественную спецификацию, и регрессор d_t статистически значимо влияет на формирование значений эндогенной переменной. Однако смысл этого утверждения изменился. Теперь следует констатировать, что затраты на обучение в специализированной школе статистически значимо отличаются от затрат в общеобразовательной школе.

Из уравнения (7.2) легко получить модели непосредственно для общеобразовательных и специализированных школ. Для этого достаточно присвоить переменной d_t значения вначале «0», а затем «1».

Очевидно, что графики этих моделей представляют собой две параллельные прямые, отстоящие друг от друга на 133259 по оси абсцисс (рис. 7.1).

Рис. 7.1. Диаграмма рассеяния и графики моделей для обычных и специализированных школ.

Фиктивные переменные часто применяются при построении динамических моделей, когда с определенного момента времени начинает действовать какой-либо качественный фактор.

Пример Модель расходов на автотранспорт в Европе в период с 1963 по 1982 годы.

Замечание. В 1974 году в Европе начался крупный нефтяной кризис, который резко поднял цены на ГСМ.

В результате в 1974 году резко снизились расходы на автотранспорт, но затем затраты вновь стали расти с прежней скоростью.

Для учета этой ситуации вводится фиктивная переменная d_t, которая равна:

На рис. 7.2. приведены исходные данные и результаты оценки модели «Расходы на ГСМ от времени».

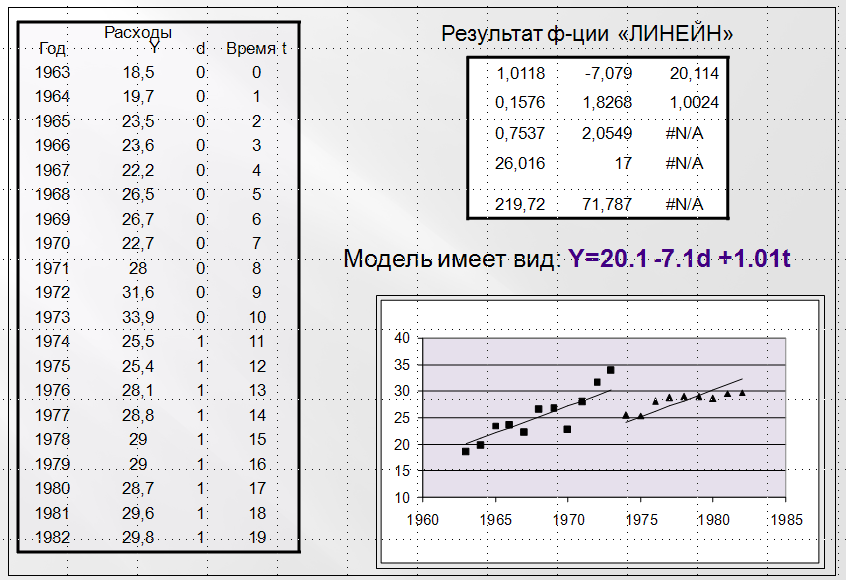
Рис. 7.2. Исходные данные и результаты оценивания модели.

Модель имеет точку разрыва, соответствующую t=1974, тренд увеличения расходов со временем остался неизменным. Статистическая значимость параметра при фиктивной переменной указывает на то, что падение расходов на ГСМ в 1974 году было статистически значимым с 95% вероятностью.

Мы рассмотрели случай, когда фиктивная переменная имеет всего две градации: общеобразовательная или специализированная школы, состояние до 1974 года и после 1974 года. На практике фиктивная переменная может иметь несколько уровней возможных значений. Школы: общеобразовательные, специализированные, технические, профессионально технические. Фиктивная переменная «регион» может иметь достаточно большое количество градаций: Москва, Белгород, Санкт-Петербург, Уфа, Екатеринбург и т.д. Очевидно, что в различных регионах России существуют различия в оплате труда, уровне средней зарплаты и т.д.

Как учесть при моделировании возможность фиктивной переменной иметь количество градаций большее двух? Оказывается, что просто присвоить каждому региону (градации) некоторый, порядковый номер, нельзя, поскольку различия в заработной плате, например, не пропорционально номеру региона в перечне. Если так поступить, то это будет означать, априори регионам будет присвоен вес, и, если у самого «бедного» регион окажется большой номер, то он обеспечит этому региону максимальное значение уровня оплаты труда.

Первое, что приходит на ум, давайте вместо одной фиктивной переменной «регион» образуем несколько фиктивных переменных, соответствующих каждой градации переменной «регион». Например:

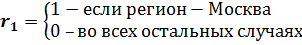
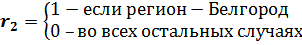
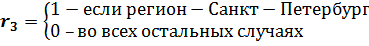
Однако если ввести все пять переменных, это приведет к ситуации, которая называется строгая мультиколлиниарность, и получить МНК-оценки параметров модели не удастся. Вспомним, одно из условий теоремы Гаусса – Маркова требует, чтобы матрица коэффициентов X была неколлинеарной, т.е. все ее столбцы были линейно независимыми от остальных. А, если воспользоваться обсуждаемым приемом, то получится следующее. Пусть спецификация модели имеет вид:

Тогда матрица коэффициентов X будет иметь вид:

(7.3)

В матрице (7.3) первый столбец состоит из единиц. Это следствие присутствия свободного коэффициента 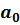в спецификации модели. Получается, что этот столбец можно представить в виде линейной комбинации 3, 4, 5, 6 столбцов:

В любой строке матрицы (7.3) всегда одно из 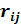будет равно единице, а все остальные нулю. В этом случае определитель матрицы равен нулю, а обратная матрица не существует.

Чтобы избежать этой ситуации предлагается вводить в спецификацию модели k-1 фиктивную переменную, где k количество градаций качественной переменной. Предполагается, что тогда k -ой градации будет соответствовать равенство нулю всех фиктивных переменных одновременно. Градацию качественной переменной, для которой все фиктивные переменные равны одновременно нулю называют базовой. Параметры при фиктивных переменных будут характеризовать превышение/снижение значения эндогенной переменной относительно базового уровня. В качестве базовой градации фиктивной переменной можно принять любую из возможных градаций качественной переменной. На практике стремятся выбрать такую градацию, относительно которой параметры модели при оставшихся фиктивных переменных имели одинаковый знак.

Продолжим рассмотрение примера построения модели «затраты на обучение от количества студентов и типа школ». В качестве градаций качественной переменной «тип школы» примем следующие: общеобразовательные, технические, ПТУ и специализированные. В качестве базовой градации примем «общеобразовательные школы». Тогда спецификация модели примет вид:

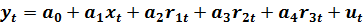(7.4)

Где: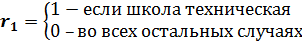

Ситуация r₁=r₂=r₃=0 будет соответствовать школам общеобразовательным (базовый уровень).

Из спецификации (7.4) можно получить спецификации моделей для каждого типа школы в отдельности:

Здесь также предполагается, что зависимость затрат на обучение от количества учащихся остается неизменной.

Оцененная модель получила вид:

(7.5)

Из (7.5) видно, что все переменные статистически значимо влияют на эндогенную переменную.

На рис. 7.3 представлены диаграмма рассеяния и графики моделей для каждого типа школ.

Рис. 7.2. Диаграмма рассеяния данных по всем школам.

Из рисунка видно, что возможно затраты на обучение в ПТУ и специализированных школах не отличаются. Расстояние между графиками моделей очень маленькое. Для того чтобы сделать обоснованный вывод о совпадении или не совпадении моделей для ПТУ и специализированных школ, необходимо проверить статистическую гипотезу . Статистические гипотезы относительно значений параметров в схеме Гаусса-Маркова проверяются с помощью критерия Стьюдента:

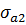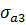В качестве стандартной ошибки приняли наименьшее значение из и . Проверка гипотезы говорит, что выдвинутую гипотезу следует принять с 95% доверительной вероятностью.

Фиктивные переменные являются эффективным инструментом при моделировании циклических процессов. Например, потребление прохладительных напитков от времени. Естественно, что их потребление зависит от времени года: зимой потребление минимально, летом – максимально. В экономике чаще всего рассматриваются периодичности в квартал или месяц. Это периоды различных видов финансовой и иной отчетности.

Рассмотрим пример модели зависимости расходов на энергоносители в США за период с января 1977г. по декабрь 1982 г. В нашем распоряжении есть поквартальные данные наблюдений. Необходимо построить модель зависимости расходов от времени с учетом поквартальных колебаний.

В качестве базовой градации фиктивной переменной «квартал» примем квартал №1. Первый квартал – это зима. Поэтому естественно предположить, что расходы на энергоносители в этот период будут максимальными. Тогда спецификацию модели можно записать в виде:

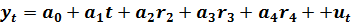(7.6)

В (7.6) фиктивные переменные r₂, r₃, r₄ равны «1» соответственно во втором, третьем и четвертом кварталах. Первое слагаемое учитывает временной тренд потребления энергоносителей.

Исходные данные для оценки модели (7.6) приведены в таб. 7.1.

Оцененная модель приняла вид:

(7.7) Очевидно, что все параметры модели (7.7) статистически значимые.

Построим график этой модели рис. 7.3. Как видно, с помощью фиктивных переменных удалось построить нелинейную модель. График – периодическая функция, подверженная небольшому положительному тренду.

Таблица 7.1.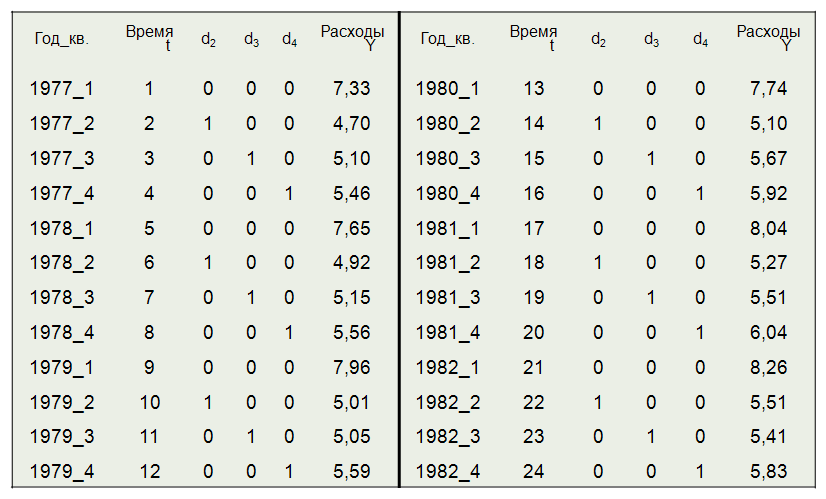

Обращают на себя внимание параметры при переменных r₂ и r₃. Значения параметров при них достаточно близкие. Имеет смысл проверить статистическую гипотезу об их равенстве:

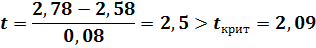
Однако предположение о равенстве параметров 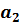и отвергается исходными данными.

Во все рассмотренных примерах предполагается, что зависимость эндогенной переменной от количественных переменных при любой градации фиктивных переменных остается неизменной. Переход фиктивной переменной с одной градации на другую вызывает скачкообразное изменение эндогенной переменной. Фиктивные переменные, которые приводят лишь к скачкообразному изменению эндогенной переменной, называются фиктивными переменными сдвига.

Рис. 7.3. Диаграмма рассеяния и график модели (7.7)

Однако на практике переход фиктивной переменной с одной градации на другую часто приводит к изменению зависимости эндогенной переменной от количественных переменных. Использование фиктивных переменных в регрессионных моделях позволяет учесть возможность такого поведения эндогенной переменной. Пусть эндогенная переменная y зависит от количественной переменной x и фиктивной переменной r. При этом есть основания предполагать, что зависимость эндогенной переменной от количественного регрессора зависит от уровня фиктивной переменной. Запишем спецификацию модели в следующем виде:

(7.8)

В спецификацию модели введено дополнительное слагаемое в виде произведения количественной и фиктивной переменных. Тогда для значений r=0 и r=1 соответственно получим уравнения:

(7.9)

Из (7.9) видно, что при r=1 в модели (7.8) одновременно изменяются значения как свободного коэффициента, так и коэффициент при регрессоре x, что приведет, как к сдвигу графика, так и к изменению угла наклона прямой.

Введение дополнительного слагаемого в спецификацию модели позволяет учесть возможность одновременного сдвига (изменение свободного коэффициента) и наклона (коэффициента при количественном регрессоре) прямой зависимости переменной y от x.

Продолжим рассмотрение примера построения модели зависимости затрат на обучение от количества учащихся в общеобразовательных и специализированных школах.

Учтем возможное изменение зависимости затрат от количества учащихся в разных школах.

Спецификацию модели запишем в виде:

(7.10)

Оцененная модель имеет вид:

График полученной модели и диаграмма рассеяния приведены на рис. 7.8.

Как видно, затраты на обучение в специализированных школах растут с числом учащихся значительно интенсивнее, чем в общеобразовательных школах.

В заключение отметим, что третье слагаемое в спецификации (7.10) называется фиктивной переменной наклона.

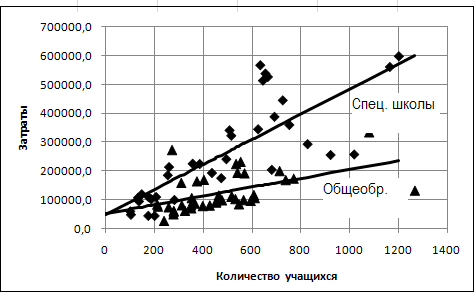
Рис. 7.8. Диаграмма рассеяния и график модели.

---

Дата добавления: 2015-10-29