
Читайте также:
|
Перш ніж безпосередньо підійти до розгляду послідовності математичної обробки рівноточних| вимірів|вимірів| виведемо декілька контрольних і допоміжних формул.
Для обчислення|підрахунку| простої арифметичної середини на практиці замість формули (5.1) зручно використовувати формулу, що має вигляд

|вид|де L0 – так званий «умовний нуль», тобто доцільно вибране наближене значення, щоб різниці

були малими величинами, δ – деяка погрішність li вимірювання. Графічна інтерпретація пошуку арифметичної середини з використанням «умовного нуля» ілюструється рис.5.4.
Дійсно, відповідно до (5.17) і (5.18) можна записати

У результаті отримана|одержувати| формула для обчислення|підрахунку| простої арифметичної середини (5.1). Далі для обчислення|підрахунку| за формулою (5.11) емпіричної середньої квадратичної| похибки необхідно спочатку за перетвореною формулою (5.8) обчислити|обчисляти| найймовірніші| поправки

| δ2 |
| … |
| … |
| … |
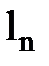
|
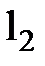
|
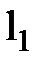
|

|

|
| Величина, яку вимірюють |
| δ1 |

|
| δn |

|

|
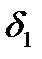
|
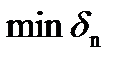
|
Евристична процедура пошуку 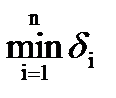
|
| Арифметична |
| середина |
Рис. 5.4 – Ілюстрація знаходження простої арифметичної середини
з використанням «умовного нуля|нуль-індикатора|»
Теоретичною перевіркою правильності обчислення арифметичної середини з використанням «умовного нуля» вимірів може служити четверта властивість арифметичної середини. Проте практика показує, що при обчисленні суми найймовірніших поправок за формулою (5.7) процедура округлення отриманих результатів дає зміщене значення L', що відрізняється від значення L на малу величину β, тобто

і зміщені поправки, також відрізняються від найймовірніших поправок на величину β.

Вищесказане проілюструємо рис. 5.5.

|

|

|
| Величина, яку вимірюють |
| Округлення |
| Проста арифметична середина L |
| Зміщене значення вимірюваної величини |
Рис. 5.5 – Ілюстрація зсуву вимірюваної величини за рахунок округлення
найймовірніших| поправок
Підсумуємо всі від  вирази (5.20) і отримаємо наступний формальний запис:
вирази (5.20) і отримаємо наступний формальний запис:

Спираючись|обпиратися| на перетворення, які зроблені при доведенні теореми
(див. п.п. 5.2) можна записати

Відповідно до п'ятої властивості арифметичної середини сума наближених поправок виміряної величини [ v' ] більше суми найймовірніших поправок [ v ]. Формально можна записати [ v' ] > [ v ].
Для знаходження незміщеного значення вимірюваної величини скористаємося виразом (5.11), який отриманий при обґрунтуванні п'ятої властивості простої арифметичної середини (див. п.п. 5.1). Замінимо в цьому виразі y на L':

Прості перетворення формул (5.19) і (5.21) дозволяють записати рівність
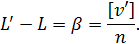
Підставляючи отримані|одержувати| вирази до формули (5.22) отримаємо наступне:

Отримана|одержувати| сума квадратів найймовірніших| поправок вимірюваної величини дорівнює різниці суми квадратів наближеної поправки і середньої величини цих же поправок. Для перевірки правильності математичних побудов знову скористаємося формулою (5.11), замінивши в ній v' на δl, а у на L0, враховуючи при цьому, що  отримаємо
отримаємо

Порівнюючи праві частини|частки| виразів (5.23) і (5.24) видно|показний|, що вони мають один і той же фізичний сенс. Оцінимо|оцінюватимемо| надійність обчислень|підрахунків| зроблених за формулою (5.12), оскільки|тому що| емпірична середня квадратична| похибка є|з'являється| величиною наближеною. Таку оцінку можна зробити, використовуючи формулу

Для визначення середньої квадратичної похибки арифметичної середини L скористаємося обґрунтуванням другої властивості простої арифметичної середини, а саме формулою (5.3). Замінимо в ній невідомі стандарти σ і σL середніми квадратичними похибками m і М, і отримаємо

На підставі отриманих|одержувати| формул (5.25) і (5.26) надійність | величини М |м-коду| можна оцінити|оцінювати|, використовуючи формулу

Розглянуті|розглядувати| вище математичні побудови|шикування| призводять|призводять| до наступної|такої| послідовності математичних процедур з обробки ряду рівноточних|лави| | вимірів|вимірів| однієї і тієї ж величини.
Процедура 1. Евристична процедура з знаходження умовного нуля L0.
Процедура 2. Процедура обчислення арифметичної середини, яка полягає в округленні отриманих результатів і визначенні величини зсуву β за формулою (5.19).
Процедура 3. Обчислення зсуву, яка полягає в округленні найймовірніших поправок v' і їх підсумовування.
Процедура 4. Контрольна перевірка правильності виконаних обчислень. Перевіряється співвідношення величини суми найймовірніших поправок ([ v' ]), отриманих процедурою 4, і добуток кількості вимірів на величину зсуву nβ. Якщо існує нерівність [ v' ] < nβ, то обчислення виконані правильно.
Процедура 5. Обчислення значень (δli)2 і (vi')2 для кожного вимірювання  і знаходження їх сум.
і знаходження їх сум.
Процедура 6. Обчислення емпіричної середньої квадратичної похибки m за формулою (5.12), спочатку на основі результатів обчислення [ v 2], отриманих за формулою (5.23), а потім на основі результатів обчислення тієї ж величини за формулою (5.24). Обидва результати повинні збігтися в межах точності вимірів.
Процедура 7. Оцінювання надійності обчислення наближеного значення емпіричної середньої квадратичної похибки результатів вимірів за формулою (5.25).
Процедура 8. Обчислення середньої квадратичної похибки простої арифметичної середини вимірюваної величини L за формулою (5.26).
Процедура 9. Оцінка надійності отриманих результатів вимірювання здійснюється за формулою (5.27).
Використовуючи наведені вище процедури розглянемо|розглядуватимемо| приклад|зразок| математичної обробки ряду|лави| незалежних рівноточних| вимірів|вимірів| величини горизонтального кута|рогу|, зроблених 16 прийомами теодолітом 2Т5.
Приклад 5.1. Результати вимірів:
L1= 115° 14' 42,1''; L7= 115° 14' 29,8''; L13= 115° 14' 32,0'';
L2= 115° 14' 35,2''; L8= 115° 14' 29,1''; L14= 115° 14' 41,4'';
L3= 115° 14' 35,4''; L9= 115° 14' 35,3''; L15= 115° 14' 21,5'';
L4= 115° 14' 34,4''; L10= 115° 14' 39,0''; L16= 115° 14' 34,6'';
L5= 115° 14' 28,7''; L11= 115° 14' 32,1'';
L6= 115° 14' 37,3''; L12= 115° 14' 27,5'';
Враховуючи рекомендації першої процедури, за значення умовного нуля приймемо величину L0=115° 14' 30,0''. Знайдемо значення величин δli=L0 – li і підсумуємо їх. Результати двох процедур наведено в табл. 5.1.
Виконуючи другу процедуру обчислимо за формулою (5.17) просту арифметичну середину, округлимо отриманий результат до 0,1'' і визначимо величину зсуву β за формулою (5.19).
Таблиця 5.1 – Вихідні дані|виміри| і проміжні результати
їх математичної обробки
| № з/п | Результати вимірів li | | δli (с) | δli2 | vi (с) | (vi')2 |
| 115° 14' 42,1'' | 12.1 | 146.4 | -8.6 | 74.0 | |
| 115° 14' 35,2'' | 5.2 | 27.0 | -1.7 | 2.9 | |
| 115° 14' 35,4'' | 5.4 | 29.2 | -1.9 | 3.6 | |
| 115° 14' 34,4'' | 4.4 | 19.4 | -0.9 | 0.8 | |
| 115° 14' 28,7'' | -1.3 | 1.7 | 4.8 | 23.0 | |
| 115° 14' 37,3'' | 7.3 | 53.3 | -3.8 | 14.4 | |
| 115° 14' 29,8'' | -0.2 | 3.7 | 13.7 | ||
| 115° 14' 29,1'' | -0.9 | 0.8 | 4.4 | 19.4 | |
| 115° 14' 35,3'' | 5.3 | 28.1 | -1.8 | 3.2 | |
| 115° 14' 39,0'' | 9.0 | 81.0 | -5.5 | 30.2 | |
| 115° 14' 32,1'' | 2.1 | 4.4 | 1.4 | 2.0 | |
| 115° 14' 27,5'' | -2.5 | 6.2 | 6.0 | 36.0 | |
| 115° 14' 32,0'' | 2.0 | 4.0 | 1.5 | 2.2 | |
| 115° 14' 41,4'' | 11.4 | 130.0 | -7.9 | 62.4 | |
| 115° 14' 21,5'' | -8.5 | 72.2 | 12.0 | 144.0 | |
| 115° 14' 34,6'' | 4.6 | 21.2 | -1.1 | 1.2 | |
| L0= 115° 14' 30,0'' | [ δl ]=55,4 | [(δli)2] =624,9 | [ vi' ]=0,6 | [(vi')2]=433,0 | |
| [ δl ]/ n =3,46'' | nβ =0,64 | ||||
| L'= 115° 14' 33,5'' | |||||
| β =0,04 |
Відповідно до третьої процедури обчислимо зсув, який утворюється за рахунок округлення найймовірніших поправок v' і підсумуємо їх
(див. стовпець 5 табл. 5.1).
Виконаємо контрольну, четверту процедуру, і порівняємо [ v' ] з величиною nβ. Результат порівняння показує, що величина [ v' ] на 0,04 менше величини nβ. Отже, обчислення виконані правильно.
П’ята процедура забезпечує обчислення квадратів (δli)2 і (vi')2.
Відповідно до шостої процедури зробимо обчислення значень емпіричної середньої квадратичної похибки m спочатку за формулами (5.12) і (5.23), а потім використовуючи формули (5.12) і (5.24).
Зробимо елементарні перетворення формули (5.12) і підставивши до неї двічі чисельні значення, отримані при обчисленні [ v2 ] за формулами (5.23) і (5.24), матимемо:
- результат обчислення|підрахунку| емпіричної середньої квадратичної| похибки із використанням чисельних розрахунків за формулою (5.23)
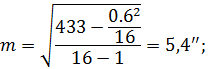
- результат обчислення|підрахунку| емпіричної середньої квадратичної| похибки із використанням чисельних розрахунків за формулою (5.24)

Рівність отриманих результатів показує правильність математичних розрахунків емпіричної середньої квадратичної похибки|підрахунків|.
Оцінювання надійності обчислення наближеного значення емпіричної середньої квадратичної похибки результатів вимірів здійснюється за сьомою процедурою із використанням формули (5.25). Підставляючи до формули чисельне значення m = 5,4'' отримаємо
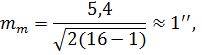
що свідчить|засвідчує| про високу надійність наближеного оцінювання емпіричної середньої квадратичної| похибки результатів вимірів|вимірів|.
Восьмою процедурою обчислюється середня квадратична| похибка знаходження простої арифметичної середини вимірюваної величини L. Підставляючи до формули (5.26) отримані чисельні значення, маємо

Остаточною, дев’ятою процедурою, здійснюється оцінювання надійності отриманих результатів вимірів. Для цього обчислюється за формулою (5.27) значення середньої квадратичної| похибки результатів вимірів
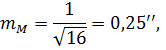
яке порівнюється з|із| сумарною ймовірною| похибкою. У нашому випадку середня квадратична| похибка майже в два з|із| половиною рази менша сумарної найймовірнішої| похибки, що свідчить|засвідчує| про задовільну надійність отриманих результатів.
Таким чином, на підставі раніше розглянутих|розглядувати| понять простої арифметичної середини і її властивостей, а також теореми про знаходження емпіричної середньої квадратичної| похибки сформована строга|сувора| послідовність математичної обробки ряду|лави| рівноточних| результатів вимірів|вимірів|. Математична обробка включає десять|десятеро| процедур, що забезпечують як обчислення|підрахунки| необхідних величин, так і контроль правильності їх виконання. Наводиться конкретний приклад математичної обробки результатів вимірів|виміру| горизонтального кута|рогу|, що показує працездатність сформованої послідовності математичних побудов|шикувань|.
Дата добавления: 2015-10-29; просмотров: 180 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формула розрахунку емпіричної середньої квадратичної| похибки | | | Нерівноточних| вимірів |