Транспортна задача

Моделі математичного програмування

Моделі лінійного програмування

Лінійне програмування – це розділ математики про методи знаходження екстремальних значень лінійної функції, на невідомі якої накладені обмеження, що виражені рівняннями чи нерівностями лінійного виду.

Розрізняють стандартну та канонічну форму запису задач лінійного програмування. При стандартній формі запису математична постановка задачі має вигляд. Знайти максимум цільової функції

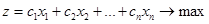(2.1.1)

при обмеженнях

............................................. (2.1.2)

; .

Канонічна форма запису відрізняється від стандартної тим, що в обмеженнях задачі замість системи нерівностей має місце система рівнянь

............................................. (2.1.3)

; .

У реальних ситуаціях може виникнути необхідність постановки задачі з обмеженнями із знаком ≥, а критерій цільової функції буде вимагати не максимізації, а мінімізації. Особливість розв”язування задач лінійного програмування полягає в тому, що універсальні методи розв”язування, зокрема симплекс-метод, розроблені для канонічної форми, тому у випадках постановки задачі, яка відрізняється від канонічної, простими математичними діями її приводять до канонічної форми запису. Наприклад, у ліву частину системи (2.1.2) вводять додаткові змінні і т.д. щоб замінити знак ≤ на =. Якщо цільову функцію (2.1.1) необхідно мінімізувати, то її замінюють на протилежну за знаком, так як . Цільова функція може мати вигляд дещо відмінний від (2.1.1). У цьому випадку можуть бути застосовані спеціальні алгоритми розв”язування задачі.

Продемонструємо на типових прикладах розв”язання задач лінійного програмування.

Транспортна задача

У загальному вигляді транспортна задача формулюється таким чином. Існує m постачальників (А₁, А_2,...A_m), які мають певну кількість деякої однорідної продукції (поставок) а_i, i= 1,2…m. Вказаний вантаж перевозиться в пункти споживання Β₁,Β₂,...Β_n, причомуобсяги споживання становлять b_j, j=1,2,...,п.

Витрати на перевезення одиниці вантажу з пункту і в пункт j становлять c_ij. Потрібно закріпити споживачів за постачальниками таким чином, щоб сумарні транспортні витрати з доставки всієї продукції споживачам були мінімальними.

Економіко-математична модель транспортної задачі має такий вигляд:

мінімізувати сумарні транспортні витрати

→ min (2.1.4)

при обмеженнях:

від кожного постачальника повинна плануватись для поставок та кількість продукції,яка у нього є в наявності

, (2.1.5)

кожному споживачеві необхідно запланувати поставку в межах необхідної йому кількості вантажу

, (2.1.6)

невід'ємності поставок

, (2.1.7)

де х_ij – шукана кількість вантажу для перевезення від і -го постачальника до j -го споживача.

Приклад. Скласти план перевезень від трьох постачальників сировини (складів) до трьох споживачів (виробників товару), якщо відома собівартість перевезень та потужності виробництва. Розрахувати сумарну собівартість перевезень. Вхідні дані представлені в таблиці 2.1.1.

Таблиця 2.1.1 – Матриця вартостей перевезень (грн) з кожного складу до кожного споживача

К-сть aij вантажу на складах, тис. т.	Потреба bij виробників товару, тис. т
В1 b1 =350	В2 b2 =400	В3 b3 =400
А1 a1 =250
А2 a2 =400
А3 a3 =700

Склад А1

Склад А2

Склад А3

виробник В1

виробник В2

виробник В3

Рис.2.1.1- Схема можливих перевезень вантажів

Для розв”язання даної задачі необхідно:

1 Перевірити її умову на так звану замкненість/відкритість моделі :

350+400+400=1150, 250+400+700=1350.

Умова не справджується, а, отже, потрібно ввести додаткового (фіктивного) споживача А₄ з потребою a₄ = 1350 -1150=200 тис.тонн вантажу. Собівартості перевезень для цього споживача мають бути нульовими (що означає – перевезення можливі тільки умовно).

2 Скласти вихідну таблицю для розв”язання задачі

	x11	x12	x13	x14
	x21	x22	x23	x24
	x31	x32	x33	x34

Цільова функція має вигляд

F(x)= 15x₁₁+17x₁₂+16x₁₃+13x₂₁+10x₂₂+12x₂₃+14x₃₁+13x₃₂+9x₃₃ ® min

3 Для розв”язання задачі методом потенціалів необхідно сформувати базисні плани, для чого може бути використаний метод північно-західного кута (діагональний), або метод найменших вартостей.

Суть методу північно-західного кута полягає у плануванні перевезень відповідно

до попиту, починаючи з першої верхньої клітки і закінчуючи крайньою нижньою (по діагоналі)

3.2 Суть методу найменших вартостей полягає у послідовному розвезенні вантажів від кожного складу (тобто по рядках, починаючи з першого) до тих споживачів, до яких собівартість перевезень найменша. Якщо попит для якогось споживача не задоволений, а собівартість не дозволяє поставити вантаж із наступного складу, то в таку клітку (A₂B₁) заносять нульову поставку. Число всіх заповнених кліток має бути m+n-1, інакше план – вироджений і не матиме розв”язку. Щоб отримати розв”язок виродженого плану, клітку A₂B₁ необхідно прирівняти до нуля

Примітка. У подальшому клітинку, в яку необхідно заносити нульову поставку, потрібно визначати, враховуючи можливість визначення потенціалів(див. п.6).

4 Перевірка на оптимальність базисних планів виконується за умовою c_ij ³ u_i + v_j для всіх кліток, де u_i і v_j – так звані потенціали, або “псевдоплатежі”, які вносять як постачальник, так і споживач за перевезення у т.ч. неіснуючих вантажів. Потенціали знаходять за такими правилами.

4.1 Вводять термінологію: клітка з вантажем – базисна клітка; клітка без вантажу – вільна клітка.

4.2 Для базисних кліток c_ij = u_i + v_j, звідки, надаючи одному з потенціалів довільного значення (наприклад 0), знаходять інші потенціали для всіх споживачів і постачальників (тобто стовпців і рядків). Значення суми потенціалів для кожної клітки проставляють у нижньому кутку клітки.

Для плану, отриманого за діагональним методом, маємо такі значення потенціалів та їх сум

					ui
				-1
				-3	-2
vj				-1

5 Оскільки клітка з координатами А₃В₁ не відповідає умові оптимальності (14 < 16), то виконуємо оптимізацію плану, вміщуючи в дану клітку вантаж (тобто перевозимо вантаж від постачальника А₃ до споживача В₁), цим самим прирівнюючи собівартість перевезень до суми потенціалів.

Для того, щоб помістити в дану клітку вантаж, його необхідно “перекинути” з інших кліток. “Перекидування” виконується із базисних кліток-вершин, які з даною вільною кліткою утворюють геометричну фігуру одного з видів

- +

-

+

- +

- - +

+ -

+ -

+ - + -

Всі вершини цих циклів мають бути розміщені у базисних клітках, окрім тієї вільної, для якої не справджується умова оптимальності.

Вершини, позначені мінусами, означають, що кількість вантажу має бути зменшена у даних базисних клітках, а вершини з плюсами означають, що у даних базисних клітках має бути збільшення кількості вантажу. У вільну клітку, для якої умова оптимальності не справджується, “перекидується” найменша кількість вантажу, яка розміщена в одній з від”ємних базисних вершин.

Після перерозподілу знову перевіряють отриманий план на оптимальність.

Для нашого прикладу отримаємо такі ітераційні таблиці:

					ui
				-1
400	100 (-)	300 (+)		-3	-2
700	(+)	100 (-)
vj				-1
					ui
250	250(-)			(+)
				-3	-4
700	100(+)			200(-)	-1
vj
					ui
					-4
				-1	-1
vj

Як бачимо, цей план після оптимізації однаковий з базисним планом, отриманим за методом найменших вартостей. Нульову поставку в клітку з координатами В₃А₂ заносять, щоб ліквідувати виродженість плану і таким чином знайти один з потенціалів.

Розв”язок цієї задачі можна отримати, використовуючи програмне забезпечення Excel, або ж Mathcad. У Mathcad 2000 Pro всі оператори набираються з палетки інструментів в меню View ®Toolbars® Math. Крім того, цей програмний продукт забезпечений текстовим редактором, який дає змогу робити необхідні пояснення до розрахунків

(Insert ®Text Region). Набір формул виконується подібно до того, як це реалізовано у редакторі формул Word, а тому особливого пояснення програма не потребує.

Інтерпретація результатів розрахунків: із складу А₁ до споживача В₁ необхідно перевезти 50 тис.тонн вантажу відповідно із складу А₂ до споживача В₂ – 400, із складу А₃ вантаж перевозять одночасно до двох споживачів В₁ і В₃ у кількості 300 тис.тонн і 400 тис.тонн.

Загальна вартість перевезень становитиме

50∙15 + 400∙10 + 300∙14 + 400∙9 = 12550 грн.

Для отримання розв”язку у Excel спочатку необхідно розмістити матриці вхідних даних у відповідних клітинках таблиці.

Спочатку створюємо таблицю вхідних даних з потужностями складів та попитом споживачів, а шуканим результатам придають нульові значення.

Нижче розміщуємо таблицю із заданою матрицею вартостей перевезень від кожного складу до кожного споживача.

Відкриваємо цільову клітинку, в яку записуємо функцію =СУММПРОИЗВ(В11:Е13;В3:Е5) для даного прикладу, тобто в дужках мають бути координати матриці перевезень вантажів з першої таблиці та матриці вартостей перевезень цих вантажів з другої таблиці.

Нижче цільової клітки записуємо всі обмеження до задачі як по горизонталі таблиці вхідних даних, так і по вертикалі цієї ж таблиці. Використовуємо функцію =СУММ(В3:Е3) для обмеження запасів на складі А₁ і так дальше

Відкриваємо із меню Сервис Надстройку Поиск решения, де записуємо координати раніше відкритої цільової клітинки і встановлюємо мітку на “Равной минимальному значению” та “изменяя ячейки $B3$E5”, тобто координати тих кліток, у які занесені нульові наближення для пошуку розв”язку.

У тому ж меню встановлюємо координати обмежень, записані за п.4. При цьому меню має такий вигляд

Команду на розрахунок посилаємо клацанням по кнопці “Выполнить”.

Результат розрахунку матиме вигляд

Дата добавления: 2015-10-28