Независимые совместные априорные нормальные-гамма распределения элементов направляющего вектора и их дисперсий

В конце предыдущей главы (раздел 2.2.4) мы заметили, что значения предполагаемых априорных дисперсий компонент направляющего вектора в критерии взвешенного метода опорных векторов является инструментом управления участием признаков в искомом решающем правиле. Это обстоятельство наводит на идею включить в число оцениваемых переменных. В этом случае критерий опорных векторов будет наделен способностью автоматически находить веса признаков, фактически отбирая их подмножество, наилучшим образом согласованное с обучающей совокупностью.

Это естественно сделать в вероятностных терминах, полагая дисперсии априори независимыми случайными величинами. Удобнее оперировать не дисперсиями , а обратными к ним величинами , называемыми мерами точности (precision measures), с априорными гамма-распределениями [3]:

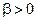Здесь и – параметры гамма-распределения, вопрос о выборе которых мы осудим ниже в разделе 3.3.

По-прежнему будем рассматривать параметрическое семейство нормальных совместных условных распределений параметров гиперплоскости относительно заданных дисперсий элементов направляющего вектора 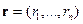и:

Тогда, вместе с априорным распределением независимых дисперсий

априорное распределение совокупности является произведением нормальных-гамма распределений [3]:

Как и прежде, будем исходить из условной плотности совместного распределения случайной обучающей совокупности относительно скрытых параметров

,

где параметр априорной разделимости классов в полагается заданным. Тогда, аналогично, апостериорное совместное распределение подлежащих оцениванию параметров модели данных относительно обучающей совокупности примет вид:

.

Отождествляя обучение, как и прежде, с вычислением байесовской оценки неизвестных параметров, мы придем к следующему критерию

являющемуся обобщением критерия.

3.2 Метод опорных векторов с релевантными компонентами:
Relevance Feature Support Vector Machine (RFSVM)

Подстановка, и в приводит к критерию обучения

Разделяющая гиперплоскость, найденная по такому критерию, сохраняет свою структуру , но отличается от тем, что веса признаков теперь вычисляются на этапе обучения, а не задаются априори.

Ключевая идея такого принципа обучения заключается в том, что при подходящем выборе параметров , алгоритм демонстрирует выраженную способность подавлять неинформативные признаки выбором маленьких, но не нулевых значений весов в разделяющей гиперплоскости. Остальные признаки с бóльшими весами предполагаются наиболее информативными (relevance features) для данной обучающей совокупности.

Прежде чем говорить об алгоритме решения задачи оптимизации, который и будет алгоритмом обучения, исследуем вопрос, как значения параметров и влияют на вид априорного гамма-распределения обратных дисперсий компонент направляющего вектора .

Известно, что математическое ожидание случайной величины, распределенной по гамма закону, равно отношению параметров , а дисперсия определяется выражением . Будем рассматривать также отношение среднеквадратичного отклонения к математическому ожиданию .

Если , априорные гамма распределения всех дисперсий сконцентрированы возле общего математического ожидания 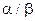(рис. 3-а). В этом случае оцененные дисперсии практически фиксированы априори и равны единице при примерно равных значениях обоих параметров 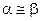. При таких значениях параметров критерий эквивалентен классическому критерию опорных векторов, использующему все признаки объектов.

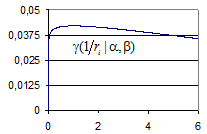
Если же , то априорные распределения становятся практически равномерными (рис. 3-б). При соответствующее слагаемое целевой функции в неограниченно уменьшается , и критерию выгодно уменьшать все дисперсии. Однако в этом случае невозможно выполнить ограничения, предписывающие достаточно хорошо аппроксимировать обучающую совокупность. В результате этого противоречия критерий проявляет ярко выраженную склонность к чрезмерной селективности отбора признаков, подавляя большинство из них, даже полезные.

, , , ,

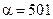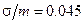
(а) (б)

Рис. 3. Вид гамма-распределения при малом (а) и большом (б) отношении .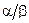

Управлять степенью селективности отбора признаков можно, варьируя значения параметров и в априорном распределении дисперсий. Будем, например, задавать эти параметры совместно по правилу

, ,

выбирая значение единственного скалярного параметра . Такой выбор параметров определяет однопараметрическое семейство гамма-распределений

.

Нетрудно убедиться, что

при ,

а также

при .

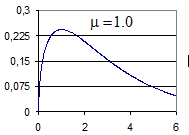
При увеличении от нуля до достаточно больших значений вид гамма-распределения плавно изменяется от сконцентрированного в окрестности 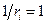до почти равномерного на неотрицательной полуоси (рис. 4). Критерий обучения, определяемый параметризацией

плавно изменяет степень своей склонности к подавлению «лишних» признаков, поэтому параметр уместно называть параметром селективности признаков в процессе обучения распознаванию образов.

Критерий по-прежнему реализует метод опорных векторов, т.е. представляет собой Support Vector Machine (SVM). В то же время этот критерий обладает способностью отбирать признаки, наиболее адекватные (релевантные) обучающей совокупности. В силу этой способности такой метод обучения уместно назвать методом опорных векторов с релевантными компонентами, или, в англоязычной терминологии, Relevance Feature Support Vector Machine (RFSVM).

Рис. 4. Зависимость априорного гамма-распределения дисперсий компонент направляющего вектора от параметра селективности.

Дата добавления: 2015-10-26