
Читайте также:
|
Обучение по прецедентам
Обучение по прецедентам:
Подмножество наблюдаемых объектов, для которых измерено значение функции 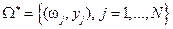 ,
, 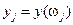 .
.
Задача: Продолжить функцию на все множество 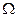 , так чтобы можно было в дальнейшем оценивать значение рассматриваемой характеристики
, так чтобы можно было в дальнейшем оценивать значение рассматриваемой характеристики 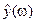 для новых объектов
для новых объектов 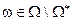 .
.
Простейшие случаи:
Задача распознавания образов
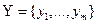 – конечное неупорядоченное множество; в частности
– конечное неупорядоченное множество; в частности 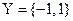 .
.
Задача восстановления числовой функции
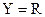 – множество действительных чисел.
– множество действительных чисел.
1.3 Концептуальная база восстановления зависимостей:
Гипотеза компактности.
Основная идея:
Выбрать в множестве объектов некоторую метрику 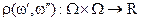
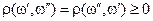 ,
, 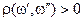 , если
, если 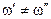 ,
, 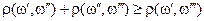
Принимать для близких объектов 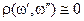 близкие решения
близкие решения
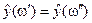 в задаче распознавания образов
в задаче распознавания образов 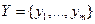
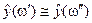 в задаче восстановления числовой зависимости
в задаче восстановления числовой зависимости 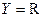
Выбор метрик удачен, если для них выполняется гипотеза компактности (Эммануил Маркович Браверман) [[1]]:
Для пар объектов 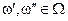 , похожих в смысле выбранной метрики
, похожих в смысле выбранной метрики 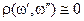 ,
,
значения целевой характеристики также в большинстве случаев близки 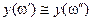 .
.
Диполь в метрическом пространстве
Метрическое пространство объектов реального мира:  ,
, 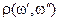 – метрика
– метрика
Диполь в метрическом пространстве – упорядоченная пара: 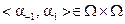
Простейшая реализация гипотезы компактности:
Принадлежность произвольного объекта к одному из двух классов
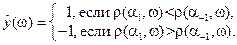 Как выбрать диполь?
Как выбрать диполь?
| В множестве объектов 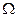 слишком мало элементов.
К тому же, наблюдатель располагает лишь конечной обучающей совокупностью объектов слишком мало элементов.
К тому же, наблюдатель располагает лишь конечной обучающей совокупностью объектов 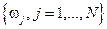
|
Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства:
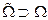 – воображаемое непрерывное метрическое пространство, в котором множество реальных объектов является подмножеством, быть может, изолированных элементов.
– воображаемое непрерывное метрическое пространство, в котором множество реальных объектов является подмножеством, быть может, изолированных элементов.
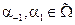 ,
, 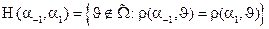 – метрическая гиперплоскость в
– метрическая гиперплоскость в 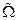
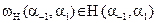 – проекция реального объекта
– проекция реального объекта 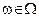 на гиперплоскость в
на гиперплоскость в 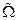
Решающая функция (score function):
расстояние точки от гиперплоскости в 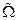 с учетом знака
с учетом знака
| 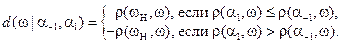
|
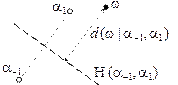
| Классификация:
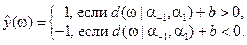 Числовая зависимость:
Числовая зависимость: 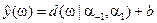
|
1.5 Идеальные условия для реализации гипотезы компактности:
Евклидова метрика в конечномерном линейном пространстве
Вектор действительных признаков 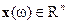 погружает множество реальных объектов в
погружает множество реальных объектов в 
Естественная евклидова метрика в 
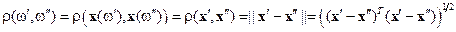
Диполь: 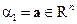 ,
, 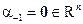 ;
;  – направляющий вектор гиперплоскости
– направляющий вектор гиперплоскости
Смещенная гиперплоскость, определяемая диполем: 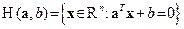 ,
, 
Решающая функция – decision (score) function:
Расстояние от точки 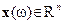 до гиперплоскости до гиперплоскости
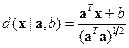 , , 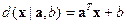 при при 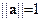
| 
|
Функция потерь: Степень несоответствия значения решающей функции значению целевой характеристики объекта
Индекс класса объекта 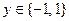 Числовая характеристика Числовая характеристика 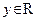
| ||
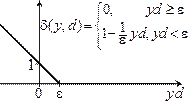
| 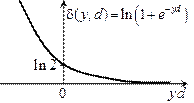
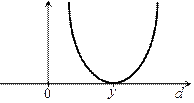
| 
|
| Двухклассовое распознавание: Метод опорных векторов | Двухклассовое распознавание: Метод логистической регрессии | Линейная модель числовой зависимости с квадратичной функцией потерь |
2 Обучение распознаванию двух классов объектов
по методу опорных векторов
Дата добавления: 2015-10-26; просмотров: 122 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Символический метод расчёта | | | Концепция оптимальной разделяющей гиперплоскости в пространстве действительных признаков объектов и классический метод опорных векторов |