Случайная величина. Непрерывные случайные величины. Функция распределения вероятностей, плотность распределения. Определение и свойства

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Непрерывные случайные величины.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Функция распределения вероятностей, плотность распределения.

· Пусть Х – непрерывная случайная величина. Функция F(x), которая определяется равенством F(x)=P(X<=x) называется функцией распределения случайной величины Х.

Свойства:

1. F (x) — непрерывная возрастающая функция.

2. ;

3. F (x ₂) – F (x ₁) = P (x ₁ < x £ x ₂)

· f(x) – плотность распределения непрерывной случайной величины

свойства:

1. f(x)>=0

2. - условие норм. плотности

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию первую производную от функции распределения :

Теорема. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу равна определенному интегралу от плотности распределения, взятому в пределах :

Свойство 1. Плотность распределения - неотрицательная функция

(

Доказательство. Функция распределения - неубывающая функция, следовательно, ее производная - функция неотрицательная.

Свойство 2. Несобственный интеграл от плотности распределения в пределах равен единице:

Доказательство. Такое событие достоверно, следовательно, вероятность его равна единице.

Числовые характеристики случайной величины. Определение математического ожидания, начальные и центральные моменты, дисперсия, среднеквадратическое отклонение, квантили случайной величины.

Часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями.

Опр. Числовыми характеристиками случайной величины называют числа, которые описывают случайную величину суммарно.

К числу важных числовых характеристик относится математическое ожидание.

Для решения многих задач достаточно знать математическое ожидание.

Опр. Математическим ожиданием дискретной случайной величины 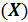называют сумму произведений всех ее возможных значений на их вероятности:

причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

для НСВ мат ожидание выглядит так:

математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Утв. математическое ожидание полностью случайную величину не характеризует, поэтому вводят и другие числовые характеристики. (такие как дисперсия).

Пример:

М (Х) = -0,01 *0,5 + 0,01* 0,5 = 0,

М (У) = -100 * 0,5 + 100 * 0,5 = 0.

Одинаковые математические ожидания, но различные возможные значения.

Отклонением называют разность между случайной величиной и ее математическим ожиданиям. .

Пусть закон распределения X известен:

X
P

отклонение имеет следующий закон распределения:

P

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

( либо док-во через раскрытие квадрата )

Свойства дисперсии в вопросе 26.

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:

Начальным моментом порядка случайной величины называют математическое ожидание величины :

Центральным моментом порядка случайной величины называют математическое ожидание величины :

При решении практических задач часто требуется найти значение x, при котором функция распределения Fx (x) случайной величины x принимает заданное значение p, т.е. требуется решить уравнение Fx (x) = p. Решения такого уравнения (соответствующие значения x) в теории вероятностей называются квантилями.
14. Распределение Пуассона и его числовые характеристики.

если проводится n(пусть n - велико) испытаний, в каждом из которых вероятность появления события А = р. Если р очень мало (р<0.1) то формула Бернулли непригодна и исползают формулу Пуассона

распределение пуассона

X			....	k
P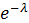

Свернули(???) по ряду Тейлора

Аналогично находим дисперсию

M[X] = λ

D[X] = λ

- среднеквадратическое отклонение

также следует заметить

Дата добавления: 2015-10-26