
|
Читайте также: |
§1. В.Д. Кулиевым предложен следующий метод суммирования рядов. Рассмотрим ряд

Если функция f(z) регулярна в правой полуплоскости Re z≥m,  z -плоскости и такова, что ее модуль при
z -плоскости и такова, что ее модуль при 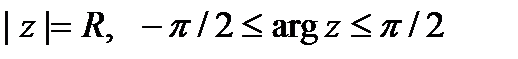 при достаточно больших R может быть как мал, так и велик, то для суммирования рядов такого типа метод Плана не применим. Поэтому возникает необходимость в разработке метода суммирования рядов, учитывающего и это обстоятельство.
при достаточно больших R может быть как мал, так и велик, то для суммирования рядов такого типа метод Плана не применим. Поэтому возникает необходимость в разработке метода суммирования рядов, учитывающего и это обстоятельство.
Обозначение. Под Sα понимается сектор, образованный двумя лучами в z -плоскости, исходящими из точки O1(m,0) симметрично относительно действительной оси под углом α (0<α≤π/2).
Теорема Кулиева. Пусть:
1°. Функция f(z) регулярна внутри и на границе сектора Sα.
2°. Функция f(z) в точках z=k, где k=m, m+1, m+2,…, не имеет нулей.
3°. Угол α такой, что предельное равенство
 (1.1)
(1.1)
выполняется равномерно по 
4°. Несобственный интеграл
 (1.2)
(1.2)
сходится.
Тогда
 (1.3)
(1.3)
где 
Этот метод в дальнейшем назовем  - метод.
- метод.
§2. Рассмотрим следующую задачу. Пусть длина стержня равна l. Направим ось x вдоль стержня так, чтобы его торцевые сечения заняли положения  и
и  . Боковую поверхность стержня будем считать теплоизолированной. Требуется найти решение уравнение теплопроводности (2.1) при граничных условиях
. Боковую поверхность стержня будем считать теплоизолированной. Требуется найти решение уравнение теплопроводности (2.1) при граничных условиях
 (2.1)
(2.1)
и начальном условии
 (2.2)
(2.2)
где  ,
,  - некоторые заданные функции. Предполагается, что функция
- некоторые заданные функции. Предполагается, что функция  определена в промежутке
определена в промежутке  и удовлетворяет на нем условиям для стержня в промежутке
и удовлетворяет на нем условиям для стержня в промежутке  .
.
Решение данной задачи известно и имеет вид:
 (2.3)
(2.3)
Формулу (2.3) можно записать так:
 (2.4)
(2.4)
Здесь
 (2.5)
(2.5)
Применяя 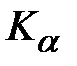 - метод суммирования рядов
- метод суммирования рядов 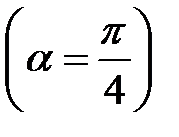 к рядам в формуле (2.5) получаем:
к рядам в формуле (2.5) получаем:
 (2.6а)
(2.6а)
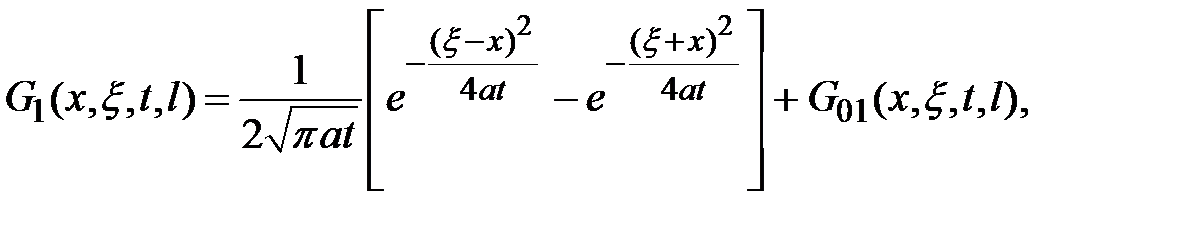

 (2.6)
(2.6)

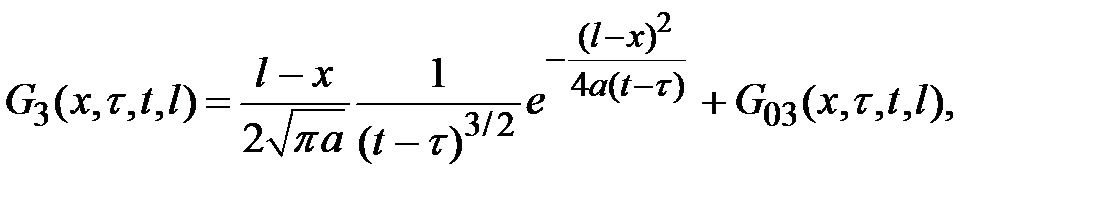

Формула (2.3) в силу равенств (2.4) и (2.6) принимает вид:
 (2.7)
(2.7)
Из (2.6) следует, что функции 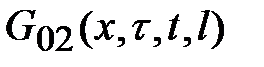 и
и  определены в промежутке
определены в промежутке  , причем
, причем

 (2.8)
(2.8)
 (2.9)
(2.9)
Вычисляя интеграл в (2.9), находим
 (2.10)
(2.10)
Из (2.7) в силу (2.8), (2.10) и (2.6а) имеем:
1º. Если  и
и  ,
,  .
.
2º. Если  и
и  ,
,  .
.
3º. Если  и
и  , то
, то
4º. Если  ,
,  и
и 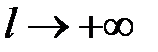 , то
, то
 (2.11)
(2.11)
Функция  , определяемая по формуле (2.11), является решением однородного уравнения
, определяемая по формуле (2.11), является решением однородного уравнения
 (2.12)
(2.12)
и удовлетворяет условиям
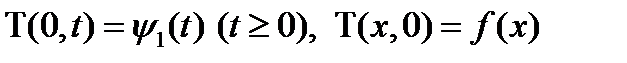 (2.13)
(2.13)
т.е. функция 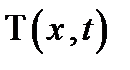 является решением задачи о распространении тепла в полуограниченном стержне с теплоизолированной боковой поверхностью
является решением задачи о распространении тепла в полуограниченном стержне с теплоизолированной боковой поверхностью  при условиях (2.13).
при условиях (2.13).
Решение данной задачи известно [ ]. Однако, предлагаемые методы его построения представляются достаточно громоздкими. Применение  – метода суммирования
– метода суммирования  к рядам (2.5) позволяет получать решение такой задачи несколько проще.
к рядам (2.5) позволяет получать решение такой задачи несколько проще.
Список литературы:
1. Кулиев В.Д. Сингулярные краевые задачи. М.: ФИЗМАТЛИТ, 2005.
Дата добавления: 2015-09-01; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Асланлы Ф.И., Дементьева Н. Г. | | | Голуненко О.И., Апалькова Т.Г. |