Теория поля

1. Оператор набла

Оператором Ñ (набла) называется псевдовектор:

¢

Ñ записывается как вектор: в виде столбца или строки с штрихом вверху - символом транспозиции, а является дифференциальным оператором. Применение оператора Ñ к некоторому объекту записывается в виде умножения на Ñ, и мы назвали его псевдовектором, поскольку все случаи его применения формально аналогичны умножению векторов. Как известно, для векторов определены три вида умножения: умножение на скаляр, скалярное произведение и векторное произведение. Соответственно, для оператора Ñ определены три операции:

Ñu =(¶u/¶x,¶u/¶y,¶u/¶z)¢ = gr(u) =

( Ñ v) = = div v

[Ñ´ v ] = = rot v

Результат первой операции называется градиент, второй – дивергенция, третьей – ротор.

2. Стандартные значения

Помня, что r = x = (x, y, z)′ - текущий радиус-вектор, 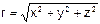- его длина, вектор dr = 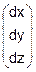- его приращение, а dr 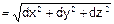- длина приращения, вычислим результаты применения оператора Ñ к нашим стандартным переменным

Ñr = r /r

div r = n, где n - размерность пространства,

rot r = [Ñ´ r ] =

3. Потенциальное поле

Поле называется потенциальным тогда и только тогда, когда существует функция u(r), такая, что v (r) = Ñu(r), при этом функция u(r) называется потенциалом поля.

Поле потенциально тогда и только тогда, когда оно безвихревое, т.е. [Ñ´ v ] = .

Для потенциальных полей du = ¶u/¶x dx + ¶u/¶y dy +¶u/¶z dz = ( Ñu d r) = (v d r)

4. Ньютоновский (кулоновский) потенціал

Функция является потенциалом для поля гравитационных сил:

поэтому функция , где А - некоторая константа, называется ньютоновским (кулоновским) потенциалом.

5.Теорема о потенциале.

Пусть нам дано некоторое дифференцируемое поле F. Тогда следующие четыре утверждения являются эквивалентными, т.е. все они выполнены или не выполнены одновременно:

1. поле F является потенциальным, т.е. существует функция u, такая, что F = Ñu

2. величина интеграла 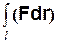определяется выбором начальной и конечной точки пути интегрирования, и не зависит от кривой, их соединяющей

3. в поле F циркуляция по любому замкнутому контуру равна нулю = 0

4. поле F является безвихревым, т.е.: rot v = [Ñ´ v ] = ≡

6.Поток вектора

Элементарным потоком dФ через малую площадку называется произведение площади площадки ds на проекцию вектора поля v в точке, где расположена площадка, на нормаль к площадке.

Если для каждой малой площадки ввести вектор площади ds = ds n, то выражение для элементарного потока примет вид

dФ = v_n ds = (v n) ds = (v ds)

Для конечной поверхности потоком называется сумма элементарных потоков через малые площадки на которые эту поверхность можно разбить, т.е. потоком вектора v через поверхность S называется двойной интеграл по этой поверхности

Ф =

7. Теорема 2 (Гаусса - Остроградского)

Пусть в трехмерной области Ω, ограниченной поверхностью S с непрерывной (или, по меньшей мере, кусочно-непрерывной) нормалью задано гладкое векторное поле v. Тогда интеграл по объему Ω от дивергенции v равен поток у v через замкнутую поверхность S.

8. Теорема Стокса

Пусть в области определения гладкого векторного поля v задана поверхность S с кусочно-непрерывной нормалью n, границей которой является кусочно-гладкая замкнутая кривая (контур) l. Тогда поток ротора v через поверхность S равен циркуляции поля v по контуру l, если при вычислении циркуляции контур проходится против часовой стрелки, если смотреть из конца нормали n.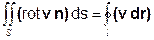

---

Дата добавления: 2015-09-05