Функции нескольких переменных

1.Частные производные

Пусть на плоскости заданы координаты (x, y). Тогда: r = (x, y)′ - текущий радиус-вектор, - его длина, вектор dr = - его приращение, а dr - длина приращения.

Пусть теперь функция F(r) =F(x,y) определена в некоторой окрестности точки r ₀(x₀,y₀). Тогда вдоль прямой, параллельной оси x она порождает в этой окрестности функцию одной переменной x, а именно F(x,y₀)=f₀(x), при этом остальные переменные (в данном случае это переменная у) играют роль параметров. Так, рассмотрим в качестве примера функцию двух переменных F(x,y)=x²y и в качестве базовой точку (x₀,y₀)=(2,2). Проведем через эту точку прямую, параллельную оси х. Вдоль такой прямой функция F=x²y порождает функцию f₀(x)=2x², ведь вдоль этой прямой везде у=2. Аналогично, если в качестве базовой выбрать точку (2,3), то получим функцию f₁(x)=3x². Т.е в обоих случаях получилась функция типа ах², причем роль параметра а играет значение координаты у в выбранной точке r ₀(x₀,y₀).

Если порожденная указанным способом функция одной переменной x F(x,y₀)=f₀(x) имеет в точке (x₀,y₀) обычную производную по x, эта производная называется частной производной первого порядка по x в точке (x₀,y₀) исходной функции двух переменных F(x,y). Эта частная производная обозначается 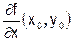или ¶F/¶x(x₀,y₀) или F¢_x(x₀,y₀).

Вполне аналогично можно определить частную производную по у как производную функции одной переменной у, которая получается из при фиксации значения первой переменной х: F(x₀,y)=f₃(у)

Или наглядно: частная производная по одной из переменных равна приросту функции при условиях, что эта переменная выросла на единицу, а все остальные переменные не менялись

2.Градиент и его свойства

Пусть n-мерный вектор, здесь символом «′» обозначена операция транспозиции, которая превращает строки в столбцы и столбцы в строки, так что

а F(x) – непрерывно дифференцируемая функция переменной x, т.е. F(x) функция n переменных x_i. Градиентом F(x) в точке x ₀ называется n-мерный вектор-столбец = , координатами которого являются частные производные F(x) по координатам x_i, вычисленные в некоторой точке x ₀.

Основные свойства:

1. Используя вектор-градиент можно записать первый дифференциал в виде скалярного произведения:

dF= ( d x) = 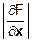│ d x│ cos φ

Здесь cos φ это косинус угла между вектором смещения d x и градиентом. Из такой формы записи следует несколько выводов:

2. Производная по любому направлению равна проекции градиента на это направление: 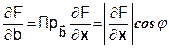т.е. произведению длины градиента на косинус угла между градиентом и вектором направления

3. Вектор градиент всегда направлен в сторону скорейшего возрастания функций.

4. В направлении перпендикулярном градиенту производная равна нулю. Поэтому градиент функции F всегда перпендикулярен к линии уровня этой функции.

5. Для линейной функции F(х) = c₁ x₁ + c₂ x₂ +.... c_n x_n = (cx) градиентом является постоянный вектор коэффициентов (c₁, c₂,.... c_n)′= c т.е. линейная функция быстрее всего растет в направлении c, и вообще растет только в тех направлениях, на которые c имеет положительную проекцию.

3. Первый дифференциал

Пусть функция многих переменных F(x) в окрестности точки x ₀ имеет непрерывные производные по всем переменным, тогда F(x) называется дифференцируемой в точке x ₀, втом и только в том случае когда ее приращение имеет вид суммы линейной формы А₁Dх₁ + А₂Dх₂ + … + А_nDх_n и некоторой ошибки e, которая есть бесконечно малая более высокого порядка, чем dr: e = o (dr); далее будем обозначать как . Получим, что функция дифференцируема в точке тогда и только тогда, когда для ее приращения справедливо пердставление:

DF=F(x ₀+ dx)– F(x ₀) = А₁dх₁ + А₂dх₂ + … + А_ndх_n + = dF(x ₀) +

При этом линейна¥ часть приращения называется первым дифференциалом:

dF(x ₀) = А₁dх₁ + А₂dх₂ + … + А_ndх_n

По определению i–й коэффициент А_i в формуле первого дифференциала называется частной производной функции F в точке x ₀ по переменной х_i.

dF(x ₀) = dx₁ + dx₂ + …+ dx_n

Вполне очевидно, что первый дифференциал может быть представленр в виде скалярного произведения вектора-градиента = на вектор смещения dF(x ₀) = ( d x)

4. Частные производные второго порядка

Если в некоторой области у F(х) существуют частные производные первого порядка, их самих можно рассматривать как функции, и у них могут существовать свои производные. Если, например, пространство трехмерно:, 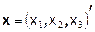, то производная функции по второй переменной есть в свою очередь функция всех трех переменных . Соответственно, она может иметь три частных производных:

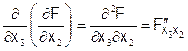
При этом производная во второй строке называется чистой второй производной, а остальные смешанными.

Если функция F(х) обладает всеми производными второго порядка, то можно построить матрицу вторых частных производных (матрицу Гессе или гессиан) по столбцам которой стоят градиенты первых частных производных

Важное свойство:

У дифференцируемых функций вторые смешанные частные производные не зависят от порядка дифференцирования: = , а значит МАТРИЦА ГЕССЕ ВСЕГДА СИММЕТРИЧНА

5. Второй дифференциал

Вполне аналогично тому, как это было сделано для функции одной переменной, вводится понятие дважды дифференцируемой функции многих переменных.

Если в окрестности данной точки приращение функции можно представить в виде суммы линейной формы относительно вектора d x: А₁dх₁ + А₂dх₂ + … + А_ndх_n, а также половины квадратичной формы относительно вектора d x: (d x¢ H (x) d x) и ошибки e, порядок малости которой выше второго − o (d x′ d x), то функция называется дважды дифференцируемой в точке x₀, линейная часть приращения называется первым дифференциалом и обозначается dF, квадратичная часть приращения (d x¢ H (x) d x)называется вторым дифференциалом и обозначается d²F:

dF(x ₀) = dx₁ + dx₂ + …+ dx_n = ( d x)

= ( d x¢ d x)

И приращение для дважды дифференцируемой функции имеет вид:

DF=F(x₀ +D x)– F(x₀)=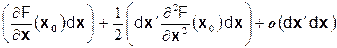

6.Условия экстремума

Стационарность: если в некоторой точке x₀ все частные производные равны нулю Û градиент равен нуль-вектору 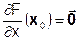Û первый дифференциал тождественно равен нулю dF ≡ 0 − то такая точка называется стационарной.

Необходимое условие экстремума − стационарность. Другими словами – в точке, в которой хоть одна из частных производных существует и не равна нулю экстремума быть не может.

Достаточное условие экстремума: второй дифференциал как квадратичная форма знакоопределен в стационарной точке.

При этом, если второй дифференциал положительно определен, в данной стационарной точке имеем минимум, если же он отрицательно определен – в данной стационарной точке имеем максимум.

Дата добавления: 2015-09-05