
Читайте также:
|
Теорема о непрерывности суперпозиции. Если функции φ i (P) (i = 1, 2, …, n) непрерывны в точке Р(t 1, t 2, …, tm)  Ω
Ω  Rm, а функция f (M) непрерывна в соответствующей точке М(x 1, x 2, …, xn) с координатами х 1= φ1(t 1, t 2, …, tm), …, хn = φ n (t 1, t 2, …, tm), то и сложная функция f (φ 1(t 1, t 2, …, t m), …, φ n (t 1, t 2, …, tm)) = f (φ 1(P), …, φ n (P)) будет непрерывна в точке Р.
Rm, а функция f (M) непрерывна в соответствующей точке М(x 1, x 2, …, xn) с координатами х 1= φ1(t 1, t 2, …, tm), …, хn = φ n (t 1, t 2, …, tm), то и сложная функция f (φ 1(t 1, t 2, …, t m), …, φ n (t 1, t 2, …, tm)) = f (φ 1(P), …, φ n (P)) будет непрерывна в точке Р.
Теорема 2. Пусть функция f (х, у) определена и непрерывна в некоторой связанной области D. Если в двух точках М0(х 0, у 0) и М1(х 1, у 1) этой области функция принимает значения разных знаков
f (х 0, у 0) < 0, f (х 1, у 1) > 0,
то в этой области найдётся точка М'(х ', у '), в которой функция обращается в ноль:
f (х ', у ') = 0.
Доказательство. Так как область D является связанной, то указанные две точки М0 и М1 можно соединить ломанной (смотри рисунок.).
Перебирая значения функции в вершинах ломаной, найдём звено, на концах которого функция f (х, у) принимает значения противоположных знаков. Составим уравнение звена, соединяющего эти две найденные вершины
х = х 0 + t ·(х 1 – х 0), у = у 0 + t ·(у 1 – у 0), 0 ≤ t ≤ 1. (1.3)
Подставив (1.3) в f (х, у), получим функцию одного переменного F(t) = f (х 0 + t ·(х1 – х 0), у 0 + t ·(у 1 – у 0)), 0 ≤ t ≤ 1. Для этой функции одного переменного имеем F(0) = f (х 0, у 0) < 0, F(1) = f (х 1, у 1) > 0. Опираясь на свойство функции одной переменной, получим существование такого значения t ', что F(t ') = 0, 0 ≤ t ' ≤ 1: F(t ') = f (х 0 + t '·(х 1 – х 0), у 0 + t '·(у 1 – у 0)) = f (х ', у ') = 0.
24) Определение векторной функции скалярного аргумента
Как известно из векторной алгебры, разложение любого вектора 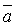 имеет вид
имеет вид
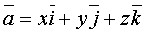 ,
,
где 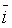 ,
, 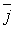 и
и 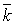 - единичные векторы, направленные по осям координат, а x, y,
- единичные векторы, направленные по осям координат, а x, y,
z – координаты вектора (проекции на оси координат). Если координаты x, y,
z – постоянные числа, то и вектор 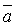 является постоянным.
является постоянным.
Пусть теперь координаты вектора являются функциями параметра t, изменяющегося в некотором интервале:
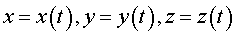 .
.
Тогда и сам вектор является переменным; при этом каждому значению параметра t будет соответствовать определённый вектор
 .
.
Определение 1
Если каждому значению параметра t (взятому из области допустимых значений функций x ( t ), y ( t ), z ( t )) соответствует определённый вектор 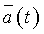 , то , то 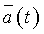 называется векторной функцией скалярного аргумента. называется векторной функцией скалярного аргумента.
|
Принято представлять вектор 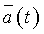 исходящим из начала координат, т. е.
исходящим из начала координат, т. е. 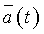 является радиус-вектором
является радиус-вектором 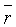 некоторой точки М.
некоторой точки М.
Если параметр будет изменяться, то конец радиус-вектора 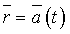 опишет некоторую линию L, которая называется годографом векторной функции
опишет некоторую линию L, которая называется годографом векторной функции 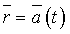 .
.
Годограф можно задать векторным уравнением
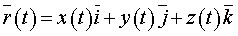 .
.
Всякую линию в пространстве можно рассматривать как годограф некоторого вектора.
Параметрические уравнения годографа:
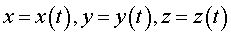 .
.
Дата добавления: 2015-08-27; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Непрерывность функции многих переменных | | | Классификация элементарных функций. |