|
Читайте также: |
При интегрировании иррациональных функций используются различные приемы. Мы рассмотрим метод рационализации подынтегрального выражения. Он заключается в выборе такой подстановки 
, которая данное подынтегральное выражение преобразует в рациональное относительно новой переменной 
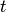. Поскольку рациональные функции мы умеем интегрировать, такие подстановки позволяют интегрировать и иррациональные функции.
Пусть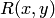 
— рациональная функция от 
и 
, т. е. функция, получаемая из 
и чисел с помощью конечного числа арифметических операций (сложения, умножения и деления).
Если заменить в 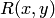переменную выражением 
, то получим функцию 
от одной переменной . Интеграл от нее имеет вид:
Этот интеграл рационализируется с помощью подстановки
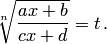
В самом деле, так как подкоренное выражение представляет собой дробно-линейную относительно функцию, то переменная рационально выражается через переменную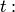 
Тогда 
— рациональная функция. Заменяя теперь переменную в данном интеграле, получим интеграл от рациональной функции новой переменной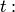
Если под знаком интеграла содержатся корни с разными показателями, но с одним и тем же дробно-линейным относительно х подкоренным выражением, то сначала следует привести их к одному показателю, после чего использовать указанный прием.
Дата добавления: 2015-08-20; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование некоторых трансцендентных функций. | | | Интегрирование гиперболических функций |