где - частное решение неоднородного, а - общее решение соответствующего однородного уравнения.

Объединяя формулы (9) и (10), получаем: общее решение неоднородного уравнения имеет вид

,

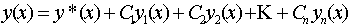где 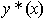- частное решение неоднородного уравнения; y ₁(х), y ₂(х) ,..., y_n (х) - фундаментальная система решений соответствующего однородного уравнения; С ₁, С ₂,..., С_n - произвольные константы.

Рассмотрим метод нахождения решения линейного неоднородного уравнения, если известно общее решение соответствующего однородного уравнения, - метод вариации произвольных постоянных.

Основная идея этого метода заключается в том, что решение неоднородного уравнения ищется в том же виде, что и общее решение (9) соответствующего однородного уравнения, но при этом константы С_i заменяются на функции С_i (х), т. е.

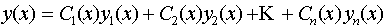. (11)

Для отыскания n неизвестных функций С_i (х) нужно иметь n условий (уравнений), причем (n - 1) условие можно выбирать достаточно произволь-

но, а последнее условие определяется тем, что функция 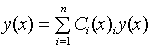должна удовлетворять уравнению (3).

Чтобы подставить функцию 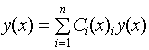в уравнение (3), нужно найти последовательно производные до порядка n, включительно. При вычислении первой производной от 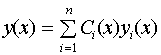для простоты полагаем, что 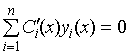и далее:

..., .

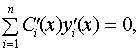
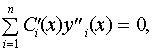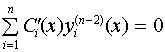C учетом этих равенств подстановка функции 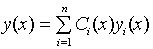и ее производных в левую часть уравнения (3) дает

L_n [ y (х)] = .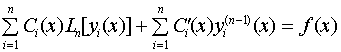

Но каждая из функций у_i (x) является решением однородного уравнения (4), значит L_n [ у_i (х)] = 0,и последнее условие принимает вид

.

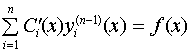Объединяя все n условий, получаем систему уравнений относительно неизвестных функций :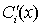

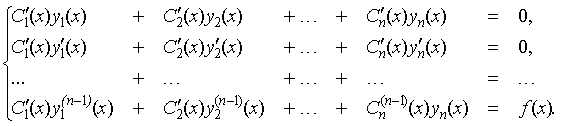(12)

Определитель D системы (12) является определителем Вронского W [ x ] для ФСР однородного уравнения, следовательно, он не равен нулю. Таким образом, система (по теореме Крамера) имеет единственное решение, которое задается формулами

,

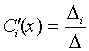где D = W [ x ], а D _i получается из определителя Вронского W [ x ] заменой i -го столбца на столбец свободных членов системы (11). При этом функции 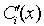непрерывны, поэтому, интегрируя их, получаем

С_i (х) = 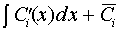, ( 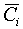- const). (13)

Подставляя функции, найденные по формулам (13), в формулу (11), получим общее решение неоднородного уравнения (3).

П р и м е р 6. Найти общее решение линейного неоднородного уравнения у¢¢ (х) + у (х) = сos ² x.

Решение. В примере 4 было найдено общее решение соответствующего однородного уравнения у¢¢ (х) + у (х) = 0. Применим метод вариации произвольных постоянных для нахождения решения неоднородного уравнения. Будем искать его в виде

у (х) = С ₁(х) sinx + C ₂(х) cosx.

Определитель Вронского

W [ sinx, cosx ] =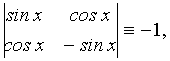

поэтому система (12) для нашего случая имеет вид

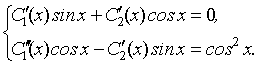
Так как

,

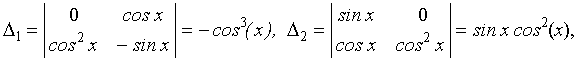то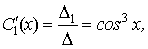

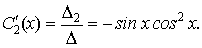
Интегрируя, найдем

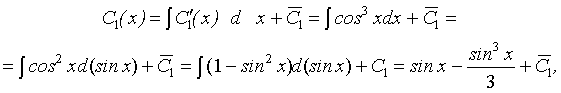
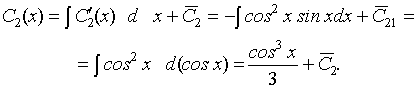
Подставим найденные значения функций С ₁(х) и С ₂(х) в формулу (11) и получим общее решение неоднородного уравнения:

у (х) = (sinx - 1/3 sin ³ x + C ₁) sinx + (1/3 cos ³ x + C ₂) cosx =

= sin ² x - 1/3 sin ⁴ x + 1/3 cos ⁴ x + C ₁ sinx + C ₂ cosx.

Здесь

C ₁ sinx + C ₂ cosx - общее решение однородного уравнения;

у* (х) = sin ² x - 1/3 sin ⁴ x + 1/3 cos ⁴ x - частное решение неоднородного уравнения.

---

Дата добавления: 2015-08-18