Тест содержал 25 заданий. Построить гистограмму.

Доступность задания x, %	25-35	35-45	45-55	55-65	65-75	75-85	85-95
Количество задач n

Решение.

Откладываем на оси абсцисс 7 отрезков длиной 10. На них, как на основаниях, строим прямоугольники, высоты которых соответственно равны 1, 1, 5, 7, 7, 3, 1. Полученная ступенчатая фигура и является искомой гистограммой.

ТЕОРИЯ ВЕРОЯТНОСТЕЙ ЧАСТЬ 2

1.СТОХАСТИЧЕСКИЙ ЭКСПЕРИМЕНТ

стохастических называют эксперименты, которые можно повторить любое количество раз, но результаты которых нельзя наверняка предсказать. В основе теоретико-множественного метода изложения теории вероятностей лежит предположение, что каждому стохастической эксперимента поставлено в соответствие некоторое множество W, точки которой изображают все возможные последствия данного эксперимента.Множество W называют пространством элементарных событий, а его точки - элементарными событиями. Таким образом, пространство элементарных событий W это совокупность всех возможных последствий стохастического эксперимента.

Пример 2. Монета подбрасывают дважды. Пространством элементарных событий этого эксперимента является множество W = {ГГ, ГР, РГ, РР}. Здесь ГР означает, например, что при первом подбрасывании появился герб, а при втором-решка.

НЕВОЗМОЖНОЕ СОБЫТИЕ

Невозмо́жным собы́тием в теории вероятностей называется событие, которое не может произойти в результате эксперимента. То есть событие, не содержащее ни одного элементарного исхода (что соответствует «пустому множеству» Ø в пространстве элементарных исходов)

ДОСТОВЕРНОЕ СОБЫТИЕ

Достове́рным собы́тием в теории вероятностей называется событие 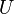, которое в результате опыта или наблюдения непременно должно произойти. Обозначается символом ^[1].

Для достоверного события 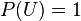, то есть вероятность события 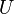равна единице.

Но, не всякое событие, вероятность которого равна 1, является достоверным (см. невозможное событие).

Если оговорена некоторая допустимая погрешность (например, 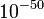), то событие, вероятность которого не более чем на значение погрешности отличается от 1, называется практически достоверным.

Пример 6. Бросают кубик. Событие - «выпало какое-то число от 1 до 6» является достоверным.

Событие называется невозможным, если оно не может произойти в данном испытании.

Пример 7. В урне находятся только черные шары. Из урны извлекают один шар. Событие - «извлечен белый шар» является невозможным.

2. ЧТО НАЗЫВАЕТСЯ (n,k)-РАЗМЕЩЕНИЕ

В комбинаторике размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.

Количество размещений из n по k, обозначаемое 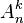, равно убывающему факториалу:

Последнее выражение имеет естественную комбинаторную интерпретацию: каждое размещение из n по k однозначно соответствует некоторому сочетанию из n по k и некоторой перестановке элементов этого сочетания; число сочетаний из n по k равно биномиальному коэффициенту , в то время как перестановок на k элементах ровно k! штук.

При k = n количество размещений равно количеству перестановок порядка n:

ЧТО НАЗЫВАЕТСЯ (n,k)-СОЧЕТАНИЕ

В комбинаторике сочетанием из 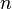по называется набор элементов, выбранных из данного множества, содержащего 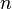различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-элементные сочетания, подмножества, 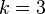) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} () являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

Число сочетаний из 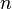по равно биномиальному коэффициенту

При фиксированном 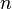производящей функцией последовательности чисел сочетаний 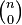, , , … является:

Двумерной производящей функцией чисел сочетаний является

3. законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения.

При табличном способе задания закона распределения первая строка таблицы содержит возможные значения случайной величины (обычно в порядке возрастания), а вторая – соответствующие вероятности ():

xi	x1	x2	…	xn
pi	p1	p2	…	pn

Бернулли: Дискретная случайная величина имеет биномиальный закон распределения (закон распределения Бернулли), если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, …, n с вероятностями, вычисляемыми по формуле Бернулли:

xi			…	m	…	n
pi	q^n		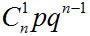…		…	p^n

где q=1-p; 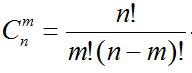- число сочетаний из n элементов по m.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

2. Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную ;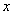
2) зависимую переменную (функцию);
3) первую производную функции: .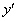

В некоторых случаях в уравнении первого порядка может отсутствовать «икс» или (и) «игрек» – важно чтобы в ДУ была первая производная 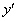, и не было производных высших порядков – 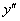, и т.д.

Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит, найти множество функций , которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.

Пример 1

Решить дифференциальное уравнение

Полный боекомплект. С чего начать решение любого дифференциального уравнения первого порядка?

В первую очередь нужно переписать производную немного в другом виде. Вспоминаем громоздкое обозначение производной: . Такое обозначение производной многим из вас наверняка казалось нелепым и ненужным, но в диффурах рулит именно оно!

Итак, на первом этапе переписываем производную в нужном нам виде:

На втором этапе всегда смотрим, нельзя ли разделить переменные? Что значит разделить переменные? Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью «школьных» манипуляций: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п.

Дифференциалы и – это полноправные множители и активные участники боевых действий. В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:

Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».

Следующий этап – интегрирование дифференциального уравнения. Всё просто, навешиваем интегралы на обе части:

Разумеется, интегралы нужно взять. В данном случае они табличные:

Как мы помним, к любой первообразной приписывается константа. Здесь два интеграла, но константу достаточно записать один раз. Почти всегда её приписывают в правой части.

Строго говоря, после того, как взяты интегралы, дифференциальное уравнение считается решенным. Единственное, у нас «игрек» не выражен через «икс», то есть решение представлено в неявном виде. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То есть, – это общий интеграл.

Теперь нужно попробовать найти общее решение, то есть попытаться представить функцию в явном виде.

Пожалуйста, запомните первый технический приём, он очень распространен и часто применяется в практических заданиях. Когда в правой части после интегрирования появляется логарифм, то константу почти всегда целесообразно записать тоже под логарифмом.

То есть, вместо записи обычно пишут .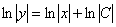

Здесь – это такая же полноценная константа, как и . Зачем это нужно? А для того, чтобы легче было выразить «игрек». Используем школьное свойство логарифмов: . В данном случае:

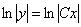
Теперь логарифмы и модули можно с чистой совестью убрать с обеих частей:

Функция представлена в явном виде. Это и есть общее решение.

Множество функций является общим решением дифференциального уравнения .

Частным решением дифференциального уравнения на интервале называется каждая функция 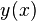, которая при подстановке в уравнение вида

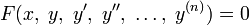
обращает его в верное тождество на интервале .

Интегральной кривой называется график решения геометрически неопределённого интеграла (первообразной), представляющего собой семейство «параллельных» кривых , где каждому числу С соответствует определенная кривая семейства. График каждой кривой и называется интегральной кривой.

3. Теорема существования и единственности решения задачи Коши

Укажем достаточные условия существования и единственности решения задачи Коши

. (1)

Теорема Пикара. Пусть функция непрерывна в прямоугольнике

и удовлетворяет условию Липшица по y равномерно относительно x, т.е. , для всех x, и .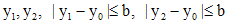

Пусть

,

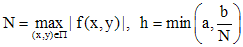тогда задача Коши (1) на промежутке имеет единственное решение .

Замечание. Условие Липшица в теореме Пикара можно заменить на требование ограниченности или непрерывности в каждом компакте из области определения дифференциального уравнения.

Решение задачи Коши при выполнении условий теоремы Пикара можно найти как предел при равномерно сходящейся последовательности функций , определяемых рекуррентным соотношением

. (2)

Оценка погрешности, получаемой при замене точного решения y(x) n- м приближением 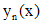, выражается неравенством

.

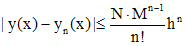Теорема Пеано. Пусть функция непрерывна в прямоугольнике , причем

.

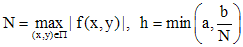Тогда задача Коши на промежутке имеет по крайне мере одно решение .

Система уравнений

в векторных обозначениях записывается в виде

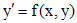, (3)

где и - векторы. Непрерывность вектор - функции f означает непрерывность всех функций , а вместо рассматривается матрица из частных производных .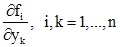

Рассмотренные выше теоремы остаются справедливы и для системы, записанной в виде (3). При этом |y| означает длину вектора y: .

Рассмотрим уравнение вида

. (4)

Пусть в области D функция f и ее частные производные первого порядка по непрерывны, и точка лежит внутри D. Тогда при начальных условиях

уравнение (4) имеет единственное решение.

Уравнение (4) можно свести к системе вида (2), если ввести новые неизвестные функции по формулам 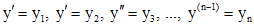. Тогда уравнение (4) сводится к системе

,

которая является частным случаем системы (3) и к которой применимы все рассмотренные утверждения.

Часто решение задачи Коши существует не только на отрезке, указанном в теоремах, но и на большем отрезке.

Если функция f(x,y) удовлетворяет в прямоугольнике условиям теоремы Пикара, то всякое ее решение можно продолжить до выхода на границу прямоугольника . Если функция f(x,y) в полосе непрерывна и удовлетворяет неравенству 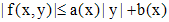, где a(x) и b(x) - непрерывные функции, то всякое решение уравнения (1) и (3) можно продолжить на весь интервал .

Пример 1. Построить последовательные приближения к решению данного уравнения с данными начальными условиями: .

Решение.

Последовательные приближения к решению данной задачи определим по рекуррентной формуле

.

Подставляя в последнюю формулу поочередно n=0,1 найдем нужные приближения:

,

.

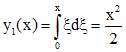4.ДУ 1-ГО ПОРЯДКА С РАЗДЕЛЯЮЩИМИ ПЕРЕМЕННЫМИ

	Дифференциальное уравнение первого порядка y' = f (x,y) называется уравнением с разделяющимися переменными, если функцию f (x,y) можно представить в виде произведения двух функций, зависящих только от x и y: где p (x) и h (y) − непрерывные функции. Рассматривая производную y' как отношение дифференциалов 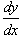, перенесем dx в правую часть и разделим уравнение на h (y): Разумеется, нужно убедиться, что h (y) ≠ 0. Если найдется число x 0, при котором h (x 0) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h (y) приводит к потере указанного решения. Обозначив , запишем уравнение в форме: Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение: где C − постоянная интегрирования. Вычисляя интегралы, получаем выражение описывающее общее решение уравнения с разделяющимися переменными.
	Пример 1
Решить дифференциальное уравнение . Решение. В данном случае p (x) = 1 и h (y) = y (y +2). Разделим уравнение на h (y) и перенесем dx в правую часть: Заметим, что при делении мы могли потерять решения y = 0 и y = −2 в случае когда h (y) равно нулю. Действительно, убедимся, что y = 0 является решением данного дифференциального уравнения. Пусть Подставляя это в уравнение, получаем: 0 = 0. Следовательно, y = 0 будет являться одним из решений. Аналогично можно проверить, что y = −2 также является решением уравнения. Вернемся обратно к дифференциальному уравнению и проинтегрируем его: Интеграл в левой части можно вычислить методом неопределенных коэффициентов: Таким образом, мы получаем следующее разложение рациональной дроби в подыинтегральном выражении: Следовательно, Переименуем константу: 2 C = C 1. В итоге, окончательное решение уравнения записывается в виде: Общее решение здесь выражено в неявном виде. В данном примере мы можем преобразовать его и получить ответ в явной форме в виде функции y = f (x,C 1), где C 1 − некоторая константа. Однако это можно сделать не для всех дифференциальных уравнений.

6.ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ БЕРНУЛЛИ

Обыкновенное дифференциальное уравнение вида:

называется уравнением Бернулли (при или получаем неоднородное или однородное линейное уравнение). При является частным случаемуравнения Риккати. Названо в честь Якоба Бернулли, опубликовавшего это уравнение в 1695 году. Метод решения с помощью замены, сводящей это уравнение к линейному, нашёл его брат Иоганн Бернулли в 1697 году.^[1]

Метод решения

Дата добавления: 2015-08-18