Функция.Предел функции и его свойства Сравнение функции.Бесконечно малые и большие величины.

функция -это зависимость, при которой каждому значению аргумента соответствует единственное значение функции.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции в точке: Число А назыв.пределом функции у=f(x) в точке а=х0 если любое Е>0,найдет такое δ=δ(Е)>0;любое х: х неравно а,удовлет.│х-а│<Е выполняется нед.│ f(x)-А│<Е →lim(х→а) f(x)=A

Свойства пределов функции:

1) Предел постоянной величины.Предел постоянной величины равен самой постоянной величине

2) Предел суммы.Предел суммы двух функций равен сумме пределов этих функций

3) Предел произведения функции на постоянную величину.Постоянный коэффициент можно выносить за знак предела

4) Предел произведения.Предел произведения двух функций равен произведению пределов этих функций

5) Предел частного.Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Свойства:1)алгебраическая сумма конечного числа бес.мал.есть величина бес.мал. 2)произведение беск.мал.на аграниченную функцию есть величина беск.мал. 3)частное от деления бес.мал.на функц.предел не равен 0 есть величина беск.мал. 4) если: предел хстремится к бесконечности бескон.мал(0)/ϕ(х) = 0;бесконечн. Если: предел хстремит.к бесконечн. Беск.мал.(х)/ϕ(х) =1,то беск.мал и ϕ эквивалентные

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Свойства:1)произвед.ББВ на функцию предел неравен 0,есть величина бескон.больш. 2)сумма ббв и ограниченной функции есть величина бескон.больш. 3)частное от деления ббв на функцию предел в точке 0 есть величина беск.больш.

14. замечательные пределы

Первый замечательный предел:

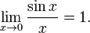
Второй замечательный предел:

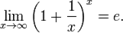
15 Алгебраическое уравнение 2-го порядка с 3-мя аргументами:

Аx^2+Вy^2+Cz^2+2Dxy+2Fyz+2Mx+2Ny+2Pz+Q=0

В пространстве оно определяет поверхности 2-го порядка. Это уравнение может быть приведено к одному из следующих случаев.

Пусть функция у = f(x) определена в точке x_0 и в некоторой окрестности этой точки. Функция y = f(x) называется непрерывной в точке x_0, если существует предел функций в этой точке и он равен значению функции в этой точке, т.е.:

lim┬(x→x_0)⁡〖f(x)=f(x_0)〗

Функция y = f(x) называется непрерывной в точке x_0, если она определена в точке x_0 и ее окрестности и выполняется равенство lim┬(∆x→0)⁡〖∆y=0〗 т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Свойства односторонних пределов:

1)Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределом вдоль фильтра.

2)Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.

Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.

Дата добавления: 2015-08-17