Непрерывность функции в точке.

Пусть функция у = f (x) определена в некоторой окрестности точки х₀, включая саму точку х₀.

Функция у = f (x) называется непрерывной в точке х₀, если она имеет предел в точке х₀, равный значению функции в этой точке, т.е.

(17.1)

Непрерывность функции у = f (x) в точке х₀ равносильна возможности представить функцию в виде f (x)= f (x₀) + a (x), где a (x) – б. м. функция при х® х₀ (см. теорему 16.4).

Дадим еще одно определение непрерывности функции на языке приращения аргумента и приращения функции, имеющее широкое применение при доказательстве непрерывности той или иной функции.

Если задана функция у = f (x), то приращением аргумента x в точке х₀ называется число

Δх= х-х_{0 ,}

отсюда х= х₀+ Δх; число Δу= f (x) –f (x₀) = f (x₀+ Δх) – f (x₀) называется приращением функции у = f (x) в точке х₀, вызванное приращением аргумента Δх (см. рис. 17.1).

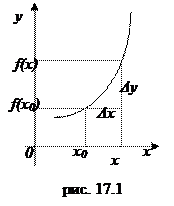Заметим еще раз, что функция у = f (x) зависит от аргумента х, а приращение функции Δу зависит от приращения аргумента Δх.

Предыдущее замечание о непрерывности функции в точке х₀ показывает, что функция у = f (x) непрерывна в точке х₀ тогда и только тогда, когда приращение функции Δу= f (x) –f (x₀) =
= f (x₀+ Δх) – f (x₀) в точке х₀ является б. м. при х® х_0, т.е. при Δх= = х-х₀® 0. Итак

(f(x) непрерывна в точке х₀) Û (),

другими словами, функция у = f (x) непрерывна в точке х₀, если бесконечно малому приращению аргумента Δх соответствует бесконечно малое приращение функции Δу.

Из определения непрерывности функции в точке вытекает важность этого понятия для вычисления пределов.

Так как , то равенство (17.1) можно записать в виде

, (17.2)

т.е. знак непрерывной функции перестановочен со знаком предела. Это означает, что при нахождении предела непрерывной функции f (x) можно перейти к пределу под знаком функции, т.е. в функцию f (x) вместо аргумента х подставить предельное значение х₀.

Дата добавления: 2015-07-20