Собственные числа и собственные векторы матрицы.

Рассмотрим квадратную матрицу А порядка n:

А= . (12.1)

Число λ называется собственным числом матрицы А, если найдется ненулевой n- мерный вектор Rⁿ, ≠ , такой, что

А =λ

(12.2)

Вектор называется собственным вектором, отвечающим собственному числу λ.

Нахождение собственных чисел и собственных векторов

Перепишем равенство (12.2) в виде

(А - λ Е) = , (12.3)

где Е=_n - единичная матрица порядка n. Равенство (12.3) представляет собой однородную систему линейных уравнений вида

(12.4)

Матрица этой системы получается из матрицы А вычитанием числа λ по главной диагонали:

А- λ Е = 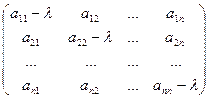(12.5)

Число λ будет собственным числом матрицы А тогда и только тогда, когда система (12.3) или (12.4) имеет нетривиальное (ненулевое) решение. А это возможно тогда и только тогда, когда матрица А- λ Е (см. (12.5)) однородной системы (12.3) (или (12.4)) вырождена, т.е. определитель этой системы равен нулю: det (A- λ E) = 0.

Поэтому собственные числа матрицы А - это корни характеристического уравнения

det (A- λ E)=0,

(12.6)

или в координатной форме

(12.7)

Если λ - собственное число матрицы А, то для нахождения соответствующих собственных векторов нужно подставить λ в систему (12.4) и найти ненулевые решения этой однородной системы, расширенная матрица которой имеет вид

= 0. (12.8)

12.2. Квадратичные формы в Rⁿ.

Квадратная матрица А порядка n называется симметричной, если А^/ = А, т.е. а_ij=a_ji (это означает симметрию относительно главной диагонали):

А =

Квадратичной формой в Rⁿ называется функция вида R

Q ()= Q (х ₁, …, х_n) = ^/ А , (12.9)

где Rⁿ, а матрица А называется матрицей квадратичной формы. Запишем определение (12.9) в координатной форме. Так как

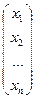= , ^/=(х ₁ х ₂ … х_n), то

Q ()=(х ₁ х ₂ … х_n) 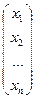= + (12.10)

Пример 12.1. Рассмотрим квадратичную форму в R ²(n =2), А = , = ,

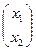^/=(х ₁ х ₂).

Тогда Q ()= Q (х ₁, х ₂)= (х ₁ х ₂) 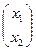=(х ₁ х ₂) =

= а ₁₁ х + а ₁₂ х ₁ х ₂+ а ₁₂ х ₁ х ₂+ а ₂₂ х = а ₁₁ х +2 а ₁₂ х ₁ х ₂ + а ₂₂ х .

Окончательно:

Q ()= Q (х ₁, х ₂)= а ₁₁ х +2 а ₁₂ х ₁ х ₂ + а ₂₂ х . (12.11)

Пример 12.2. n =3. Тогда

А = , = R ³, ^/=(х ₁ х ₂ х ₃) и Q ()= Q (х ₁, х ₂, х ₃)=

=(х ₁ х ₂ х ₃) = а ₁₁ х + а ₂₂ х + а ₃₃ х 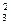+2 а ₁₂ х ₁ х ₂+2 а ₁₃ х ₁ х ₃+2 а ₂₃ х ₂ х ₃ (12.12)

Квадратичная форма Q () называется положительно определенной, если для любого ненулевого вектора Rⁿ, ≠ , выполняется условие: Q ()>0, и отрицательно определяемой, если Q ()<0.

Теорема 12.1. (Критерий положительной (отрицательной) определенности квадратичной формы).

1) Квадратичная форма положительно определена тогда и только тогда, когда все собственные числа матрицы квадратичной формы положительны.

2) Квадратичная форма отрицательно определена тогда и только тогда, когда все собственные числа матрицы квадратичной формы отрицательны.

Рассмотрим матрицу А квадратичной формы Q ()= ^/ А :

А=

Выделены миноры

∆₁₌ а _11, ∆₂= , …, ∆ _r , …, ∆ _n =∆= (12.13)

называются главными минорами матрицы А. Тогда справедлива

Теорема12.2. (Критерий Сильвестра)

1) Квадратичная форма положительно определена тогда и только тогда, когда все главные миноры матрицы квадратичной формы положительны: ∆ _i >0, i =1, …, n.

2) Квадратичная форма отрицательно определена тогда и только тогда, когда главные миноры чередуют знак, начиная со знака минус: ∆₁<0,∆₂>0,∆₃<0, …

Дата добавления: 2015-07-20